Hyperbola | Mathematics (Maths) for JEE Main & Advanced PDF Download
HYPERBOLA
The Hyperbola is a conic whose eccentricity is greater than unity. (e > 1).
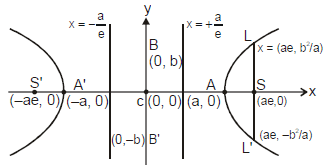
A. Standard Equation & Definition(s)
Standard equation of the hyperbola is
-
= 1, where b2 = a2(e2 - 1)
or a2 e2 = a2 + b2 i.e. e2 = 1 +
= 1 +
(a) Foci : S  (ae, 0) & S'
(ae, 0) & S'  (- ae, 0).
(- ae, 0).
(b) Equations of directrices :
(c) Vertices : A  (a, 0) & A'
(a, 0) & A'  (- a, 0).
(- a, 0).
(d) Latus rectum :
(i) Equation : x = ± ae
(ii) Length = =
= 2a (e2 - 1) = 2e (distance from focus to directrix)
(iii) Ends :
(e) (i) Transverse Axis : The line segment A'A of length 2a in which the foci S' & S both lie is called the Transverse Axis of the Hyperbola.
(ii) Conjugate Axis : The line segment B'B between the two points B' ≡ (0, -b) & B ≡ (0, b) is called as the Conjugate Axis of the Hyperbola.
The Transverse Axis & the Conjugate Axis of the hyperbola are together called the Principal axes of the hyperbola.
(f) Focal Property : The difference of the focal distances of any point on the hyperbola is constant and equal to transverse axis i.e. = 2a. The distance SS' = focal length.
(g) Focal distance : Distance of any point P(x, y) on Hyperbola from foci PS = ex - a & PS' = ex + a.
Ex.1 Find the equation of the hyperbola whose directrix is 2x + y = 1, focus (1, 2) and eccentricity .
Sol. Let P(x, y) be any point on the hyperbola and PM is perpendicular from P on the directrix.
Then by definition SP = e PM ⇒ (SP)2 = e2 (PM)2 ⇒ (x - 1)2 + (y - 2)2 = 3
⇒ 5(x2 + y2 - 2x - 4y + 5) = 3(4x2 + y2 + 1 + 4xy - 2y - 4x)
⇒ 7x2 - 2y2 + 12 xy - 2x + 14y - 22 = 0 which is the required hyperbola.
Ex.2 The eccentricity of the hyperbola 4x2 - 9y2 - 8x = 32 is
Sol.
4x2 - 9y2 - 8x = 32
⇒ 4(x - 1)2 - 9y2 = 36
⇒ -
= 1
Here a2 = 9, b2 = 4
 eccentricity e =
eccentricity e = =
=
Ex.3 If foci of a hyperbola are foci of the ellipse +
= 1. If the eccentricity of the hyperbola be 2, then its equation is
Sol. For ellipse e = , so foci = (± 4, 0)
For hyperbola
Hence equation of the hyperbola is 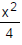 -
- = 1
Ex.4 Find the coordinates of foci, the eccentricity and latus-rectum, equations of directrices for the hyperbola 9x2 - 16y2 - 72x + 96y - 144 = 0
Sol.
Equation can be rewritten as -
= 1 so a = 4, b = 3
b2 = a2(e2 - 1) given e =
Foci : X = ± ae, Y = 0 gives the foci as (9, 3), (-1, 3)
Centre : X = 0, Y = 0 i.e. (4, 3)
Directrices : X = ± i.e. x - 4 =
 directrices are 5x - 36 = 0; 5x - 4 = 0
directrices are 5x - 36 = 0; 5x - 4 = 0
Latus-rectum
B. Conjugate Hyperbola
Two hyperbolas such that transverse & conjugate axes of one hyperbola are respectively the conjugate & the transverse axes of the other are called Conjugate Hyperbolas of each other.
eg. -
= 1 & -
+
= 1 are conjugate hyperbolas of each other.
Note :
(i) If e1 & e2 are the eccentricities of the hyperbola & its conjugate then e1-2 + e2-2 = 1.
(ii) The foci of a hyperbola and its conjugate are concyclic and form the vertices of a square.
(iii) Two hyperbolas are said to be similar if they have the same eccentricity.
Ex.5 The eccentricity of the conjugate hyperbola to the hyperbola x2 - 3y2 = 1 is
Sol.
Equation of the conjugate hyperbola to the hyperbola x2 - 3y2 = 1 is -x2 + 3y2 = 1
⇒
Here a2 = 1, b2 = 1/3
 eccentricity e =
eccentricity e =
C. Rectangular or Equilateral Hyperbola
The particular kind of hyperbola in which the lengths of the transverse & conjugate axis are equal is called an Equilateral Hyperbola. Note that the eccentricity of the rectangular hyperbola is and the length of it's latus rectum is equal to it's transverse or conjugate axis.
D. Auxiliary Circle
A circle drawn with centre C & T.A. as a diameter is called the Auxiliary Circle of the hyperbola. Equation of the auxiliary circle is x2 + y2 = a2.
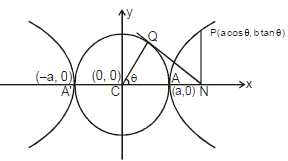
Note from the figure that P & Q are called the "Corresponding Points" on the hyperbola & the auxiliary circle `θ' is called the eccentric angle of the point `P' on the hyperbola. 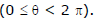
Parametric Equation : The equations x = a secθ & y = b tanθ together represents the hyperbola -
= 1 where θ is a parameter. The parametric equations ; x = a cos h φ, y = b sin h φ also represents the same hyperbola.
General Note : Since the fundamental equation to the hyperbola only differs from that to the ellipse in having -b2 instead of b2 it will be found that many propositions for the hyperbola are derived from those for the ellipse by simply changing the sign of b2.
E. Position of a point `p' w.r.t a Hyperbola
The quantity -
= 1 is positive, zero or negative according as the point (x1, y1) lies outside, upon or within the curve.
F. Line and a Hyperbola
The straight line y = mx + c is a secant, a tangent or passes outside the hyperbola  -
- = 1 according as : c2 > = < a2m2 - b2.
Equation of a chord of the hyperbola -
= 1 joining its two points P(α) & Q(β) is
cos
-
sin
= cos
Ex.6 Show that the line x cos α + y sin α = p touches the hyperbola - = 1 if a2 cos2 α - b2 sin2 α = p2.
Sol. The given line is x cos α + y sin α = p ⇒ y sin α = -x cos α + p ⇒ y = - x cot α + p cosec α Comparing this line with y = mx + c where m = - cot α, c = p cosec α
Since the given line touches the hyperbola - = 1 then c2 = a2m2 - b2
⇒ p2 cosec2 α = a2 cot2 α - b2 or p2 = a2 cos2 α - b2 sin2 α
Ex.7 If (a sec θ, b tanθ) and (a secφ, b tanφ) are the ends of a focal chord of -
= 1, then tan
tan
equal to
Sol. Equation of chord connecting the points (a sec θ, b tanθ) and (a sec φ, b tan φ) is
cos
-
sin
= cos
.........(i)
If it passes through (ae, 0); we have, e cos = cos
⇒ e =
⇒ tan.tan
=
Similarly if (i) passes through (-ae, 0), tan. tan =
G. Tangent to the Hyperbola -
= 1
(a) Point form : Equation of the tangent to the given hyperbola at the point (x1, y1) is .
Note : In general two tangents can be drawn from an external point (x1, y1) to the hyperbola and they are y - y1 = m1 (x - x1) & y - y1 = m2 (x - x2), where m1 & m2 are roots of the equation (x12 - a2) m2 - 2x1y1 m + y12 + b2 = 0. If D < 0, then no tangent can be drawn from (x1 y1) to the hyperbola.
(b) Slope form : The equation of tangents of slope m to the given hyperbola is y = mx ± .
Point of contact are
Note : There are two parallel tangents having the same slope m.
(c) Parametric form : Equation of the tangent to the given hyperbola at the point (a sec θ, b tanθ) is .
Note : Point of intersection of the tangents at θ1 & θ2 is x = a, y = b tan
Ex.8 Find the equation of the tangent to the hyperbola x2 - 4y2 = 36 which is perpendicular to the line x - y + 4 = 0
Sol. Let m be the slope of the tangent. Since the tangent is perpendicular to the line x - y = 0
 m × 1 = - 1 ⇒ m = - 1
m × 1 = - 1 ⇒ m = - 1
Since x2 - 4y2 = 36 or -
= 1. Comparing this with
 a2 = 36 and b2 = 9
a2 = 36 and b2 = 9
So the equation of tangents are y = (-1)x ±
⇒ y= - x ± ⇒ x + y ± = 0
Ex.9 The locus of the point of intersection of two tangents of the hyperbola if the product of their slopes is c2, will be
Sol. Equation of any tangent of the hyperbola with slope m is y = mx ±
If it passes through (x1, y1) then (y1 - mx1)2 = a2m2 - b2
⇒ (x12 - a2) m2 - 2x1y1m + (y12 + b2) = 0
If m = m1, m2 then as given m1m2 = c2 ⇒ = c2.
Hence required locus will be y2+b2 = c2(x2 - a2)
Ex.10 A common tangent to 9x2 - 16y2 = 144 and x2 + y2 = 9 is
Sol.
-
= 1, x2 + y2 = 9
Equation of tangent y = mx + (for hyperbola)
Equation of tangent y = m'x + 3 (circle)
For common tangent m = m' and 3or 9 + 9m2 = 16m2 - 9 or 7m2 = 18 ⇒ m=±3
 required equation is
required equation is or
H. Normal to the Hyperbola -
= 1
(a) Point form : The equation of the normal to the given hyperbola at the point P (x1, y1) on it is +
= a2 - b2 = a2 e2.
(b) Slope form : The equation of normal of slope m to the given hyperbola is y = mx foot of normal are
(c) Parametric form : The equation of the normal at the point P (a sec θ, b tanθ) to the given hyperbola is +
= a2 + b2 = a2 e2.
Ex.11 Line x cosα + y sinα = p is a normal to the hyperbola -
= 1, if
Sol. Equation of a normal to the hyperbola is ax cosθ + by cot θ = a2 + b2 comparing it with the given line equation
=
=
⇒ sec θ = ,
tanθ =
Eliminating θ , we get -
= 1
⇒ a2 sec2 α - b2 cosec2 α =
Ex.12 The normal to the hyperbola = 1 meets the axes in M and N, and lines MP and NP are drawn at right angles to the axes. Prove that the locus of P is hyperbola (a2x2 - b2y2) = (a2 + b2)2.
Sol. Equation of normal at any point Q is ax cosθ + by cot θ = a2 + b2
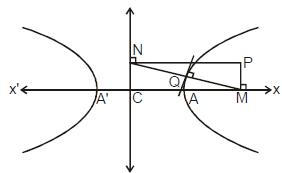
 M
M 
, N
 Let P
Let P  (h, k)
(h, k)
⇒
⇒
 locus of P is (a2x2 - b2y2) = (a2 + b2).
locus of P is (a2x2 - b2y2) = (a2 + b2).
I. Highlights on Tangent and Normal
(a) Locus of the foot of the perpendicular drawn from focus of the hyperbola -
= 1 upon any tangent is its auxilliary circle i.e. x2 + y2 = a2 & the product of lengths these perpendiculars is b2 (semi Conjugate Axis)2
(b) The portion of the tangent between the point of contact & the directrix subtends a right angle at the corresponding focus.
(c) The tangent & normal at any point of a hyperbola bisect the angle between the focal radii. This spells the reflection property of the hyperbola as "An incoming light ray" aimed towards one focus is reflected from the outer surface of the hyperbola towards the other focus. It follows that if an ellipse and a hyperbola have the same foci, they cut at right angles at any of their common point.
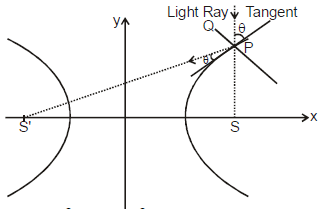
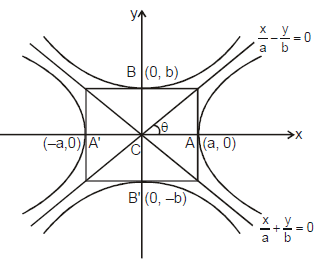
Note that : the ellipse 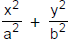 = 1 & the hyperbola
= 1 & the hyperbola -
= 1 (a > k > b > 0) are confocal and therefore orthogonal.
(d) The foci of the hyperbola and the points P and Q in which any tangent meets the tangents at the vertices are concyclic with PQ as diameter of the circle.
J. Director Circle
The locus of the intersection of tangents which are at right angles is known as the Director Circle of the hyperbola. The equation of the director circle is : x2 + y2 = a2 - b2.
If b2 < a2 this circle is real ; if b2 = a2 the radius of the circle is zero & it reduces to a point circle at the origin. In this case the centre is the only point from which the tangents at right angles can be drawn to the curve.
If b2 > a2, the radius of the circle is imaginary, so that there is no such circle & so no tangents at right angle can be drawn to the curve.
Note : Equation of chord of contact, chord with a given middle point, pair to tangents from an external point are to be interpreted in the similar way as in ellipse.
K. Asymptotes
Definition : If the length of the perpendicular let fall from a point on a hyperbola to a straight line tends to zero as the point on the hyperbola moves to infinity along the hyperbola, then the straight line is called the Asymptote of the Hyperbola.
To find the asymptote of the hyperbola :
Let y = mx + c is the asymptote of the hyperbola -
= 1.
Solving these two we get the quadratic as (b2 - a2m2) x2 - 2a2 mcx - a2(b2 + c2) = 0 ........(1)
In order that y = mx + c be an asymptote, both roots of equation (1) must approach infinity, the conditions for which are : coeff of x2 = 0 & coeff of x = 0.
⇒ b2 - a2m2 = 0 or
a2 mc = 0
⇒ c = 0.
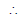 equations of asymptote are
equations of asymptote are and
combined equation to the asymptotes
Particular Case :
When b = a the asymptotes of the rectangular hyperbola. x2 - y2 = a2 are y = ± x which are at right angles.
Note :
(i) Equilateral hyperbola ⇔ rectangular hyperbola.
(ii) If a hyperbola is equilateral then the conjugate hyperbola is also equilateral
(iii) A hyperbola and its conjugate have the same asymptote.
(iv) The equation of the pair of asymptotes differ the hyperbola & the conjugate hyperbola by the same constant only.
(v) The asymptotes pass through the centre of the hyperbola & the bisectors of the angles between the asymptotes are the axes of the hyperbola.
(vi) The asymptotes of a hyperbola are the diagonals of the rectangle formed by the lines drawn through the extremities of each axis parallel to the other axis.
(vii) Asymptotes are the tangent to the hyperbola from the centre.
(viii) A simple method to find the co-ordinates of the centre of the hyperbola expressed as a general equation of degree 2 should be remembered as : Let f(x, y) = 0 represents a hyperbola.
Find &
. Then the point of intersection of
= 0 &
= 0 gives the centre of the hyperbola.
Ex.13 Find the asymptotes of the hyperbola 2x2 + 5xy + 2y2 + 4x + 5y = 0. Find also the general equation of all the hyperbolas having the same set of asymptotes.
Sol.
Let 2x2 + 5xy + 2y2 + 4x + 5y + λ = 0 be asymptotes. This will represent two straight line so
λ = 2
⇒ 2x2 + 5xy + 2y2 + 4x + 5y + 2 = 0 are asymptotes
⇒ (2x + y + 2) = 0 and (x + 2y + 1) = 0 are asymptotes
and 2x2 + 5xy + 2y2 + 4x + 5y + c = 0 is general equation of hyperbola.
Ex.14 Find the hyperbola whose asymptotes are 2x - y = 3 and 3x + y - 7 = 0 and which passes through the point (1, 1).
Sol. The equation of the hyperbola differs from the equation of the asymptotes by a constant
⇒ The equation of the hyperbola with asymptotes 3x + y - 7 = 0 and 2x - y = 3 is
(3x + y - 7)(2x - y - 3) + k = 0. It passes through (1, 1) ⇒k = -6.
Hence the equation of the hyperbola is (2x - y - 3) (3x + y - 7) = 6.
L. Highlights on Asymptotes
(a) If from any point on the asymptote a straight line be drawn perpendicular to the transverse axis, the product of the segments of this line, intercepted between the point & the curve is always equal to the square of the semi conjugate axis.
(b) Perpendicular from the foci on either asymptote meet it in the same points as the corresponding directrix & the common points of intersection lie on the auxiliary circle.
(c) The tangent at any point P on a hyperbola -
= 1 with centre C, meets the asymptotes in Q and R and cuts off a ΔCQR of constant area equal to ab from the asymptotes & the portion of the tangent intercepted between the asymptote is bisected at the point of contact. This implies that the locus of centre of the circle circumscribing the ΔCQR in case of a rectangular hyperbola is the hyperbola itself & for a standard hyperbola the locus would be the curve,
4(a2x2 - b2y2) = (a2 + b2)2.
(d) If the angle between the asymptote of a hyperbola -
= 1 is 2θ then the eccentricity of the hyperbola is secθ.
M. Rectangular Hyperbola
Rectangular hyperbola referred to its asymptotes as axis of coordinates.
(a) Equation is xy = c2 with parametric representation
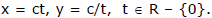
(b) Equation of a chord joining the points P(t1) & Q(t2) is x + t1 t2 y = c (t1 + t2) with slope m =
(c) Equation of the tangent at P (x1, y1) is +
= 2 & at P(t) is
+ ty = 2c.
(d) Equation of normal is y - = t2 (x - ct)
(e) Chord with a given middle point as (h, k) is kx + hy = 2hk.
Note : For the hyperbola xy = c2
(i) Vertices : (c, c) & (-c, -c).
(ii) Foci :
(iii) Directrices : x + y = ±
(iv) Latus rectum : l = = T . A = C . A
Ex.15 A triangle has its vertices on a rectangular hyperbola. Prove that the orthocentre of the triangle also lies on the same hyperbola.
Sol. Let t1, t2 and t3 are the vertices of the triangle ABC, described on the rectangular hyperbola xy = c2.
 co-ordinates of A, B and C are
co-ordinates of A, B and C are respectively
Now slope of BC is =
 Slope of AD is t2t3
Slope of AD is t2t3
Equation of altitude AD is y - = t2t3(x - ct1)
or t1y - c = xt1t2t3 - .........(i)
Similarly equation of altitude BE is
t2y - c = xt1t2t3 - .........(ii)
Solving (i) and (ii), we get the orthocentre which lies on xy = c2.
Ex.16 Chords of the circle x2 + y2 = a2 touches the hyperbola x2/a2 - y2/b2 = 1. Prove that locus of their middle point is the curve (x2 + y2)2 = a2x2 - b2y2.
Sol. Let (h, k) be the mid-point of the chord of the circle x2 + y2 = a2,
so that its equation by T = S1 is hx + ky = h2 + k2 or
i.e. of the form y = mx + c. It will touch the hyperbola if c2 = a2m2 - b2
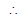
= a2
or (h2 + k2)2 = a2h2 - b2k2
Generalizing, the locus of mid-point (h, k) is (x2 + y2)2 = a2x2 - b2y2
Ex.17 C is the centre of the hyperbola -
= 1. The tangent at any point P on this hyperbola meets the straight lines bx - ay = 0 and bx + ay = 0 in the points Q and R respectively. Show that CQ . CR = a2 + b2.
Sol. P is (a cosθ, b tanθ)
Tangent at P is -
= 1.
It meets bx - ay = 0 i.e. =
in Q
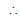 Q is
Q is .
It meets bx + ay = 0 i.e. =
in R.
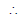 R is
R is
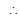 CQ.CR =
CQ.CR =
 sec2q - tan2q = 1
sec2q - tan2q = 1
Ex.18 A circle of variable radius cuts the rectangular hyperbola x2 - y2 = 9a2 in points P, Q, R and S. Determine the equation of the locus of the centroid of triangle PQR.
Sol. Let the circle be (x - h)2 + (y - k)2 = r2 where r is variable. Its intersection with x2 - y2 = 9a2 is obtained by putting y2 = x2 - 9a2.
x2 + x2 - 9a2 - 2hx + h2 + k2 - r2 = 2k
or [2x2 - 2hx + (h2 + k2 - r2 9a2)]2 = 4k2(x2 - 9a2) or 4x4 - 8hx3 + ....... = 0
 Above gives the abscissas of the four points of intersection.
Above gives the abscissas of the four points of intersection.
⇒ x1 + x2 + x3 + x4 = 2h.
Similarly y1 + y2 + y3 + y4 = 2k
Now if (α,β) be the centroid of ΔPQR, then 3α = x1 + x2 + x3, 3β = y1 + y2 + y3
 x4 = 2h - 3a, y4 = 2k - 3β
x4 = 2h - 3a, y4 = 2k - 3β
But (x4, y4) lies on x2 - y2 = 9a2
 (2h - 3a)2 + (2k - 3b)2 = 9a2
(2h - 3a)2 + (2k - 3b)2 = 9a2
Hence the locus of centroid (α,β) is (2h - 3x)2 + (2k - 3y)2 = 9a2 or
Ex.19 If a circle cuts a rectangular hyperbola xy = c2 in A, B, C, D and the parameters of these four points be t1, t2 , t3 and t4 respectively, then prove that
(a) t1t2t3t4 = 1
(b) The centre of mean position of the four points bisects the distance between the centres of the two curves.
Sol. (a) Let the equation of the hyperbola referred to rectangular asymptotes as axes by xy = c2 or its parametric equation be
x = ct, y = c/t ...........(i)
and that of the circle be x2 + y2 + 2gx + 2fy + k = 0 ...........(ii)
Solving (i) and (ii), we get
c2t2 + + 2gct + 2f
+ k = 0 or
c2t4 + 2gct3 + kt2 + 2f ct + c2 = 0 ...........(iii)
Above equation being of fourth degree in t gives us the four parameters t1, t2, t3, t4 of the points of intersection.
 t1 + t2 + t3 + t4 = -
t1 + t2 + t3 + t4 = - ...........(iv)
t1t2t3 + t1t2t4 + t3t4t1 + t3t4t2 = ...........(v)
t1t2t3t4 = = 1. It proves (a) ...........(vi)
Dividing (v) by (vi), we get ...........(vii)
(b) The centre of mean position of the four points of intersection is
=
, by (iv) and (vii) = (- g/2, - f/2)
Above is clearly the mid-point of (0, 0) and (- g, - f) i.e. the join of the centres of the two curves.
|
176 videos|582 docs|160 tests
|
FAQs on Hyperbola - Mathematics (Maths) for JEE Main & Advanced
| 1. What is a hyperbola in mathematics? |  |
| 2. How is a hyperbola different from an ellipse? |  |
| 3. What are the key features of a hyperbola? |  |
| 4. How can you graph a hyperbola on a coordinate plane? |  |
| 5. What are some real-world applications of hyperbolas? |  |

















