Chapter : Data Representation In Computer Memory, PPT, Semester, Engineering - Electronics and Communication Engineering (ECE) PDF Download
DATA REPRESENTATION
IN COMPUTER MEMORY
SUMMARY: This topic introduces the numbering systems: decimal, binary, octal and hexadecimal. The topic covers the conversion between numbering systems, binary arithmetic, one's complement, two's complement, signed number and coding system. This topic also covers the digital logic components.
CLO 2:apply appropriate method to solve arithmetic problem in numbering system (C3).
DATA REPRESENTATION IN COMPUTER MEMORY ------------------------------------------ Next Slide
2.1 Understand data representation on CPU.
2.1.1 Define decimal, binary, octal and hexadecimal number.
2.1.2 Perform arithmetic operation (addition and subtraction) in different number bases.
2.1.3 Convert decimal, binary, octal and hexadecimal numbers to different bases and vice-versa
DATA REPRESENTATION IN COMPUTER MEMORY ------------------------------------------ Next Slide
INTRODUCTION
The binary system and decimal system is most important in digital system.
Decimal - Universally used to represent quantities outside a digital system.
Its means, there will be situations decimal values must be converted to binary values before entered to digital system.
Example : Calculator / Computer
DATA REPRESENTATION IN COMPUTER MEMORY ------------------------------------------ Next Slide
DECIMAL NUMBERING SYSTEM
Decimal system is composed of 10 numerals or symbols.
These 10 sysmbols are 0, 1, 2, 3, 4, 5, 6, 7, 8, 9.
Using these symbols as digits of a number, it can express any quantity.
DATA REPRESENTATION IN COMPUTER MEMORY ------------------------------------------ Next Slide
Base number = 10
Basic number = 0,1,2,3,4,5,6,7,8,9
23410
Basic number
Base number
DATA REPRESENTATION IN COMPUTER MEMORY ------------------------------------------ Next Slide
Positional Values (weights)
2746.210 is from calculation below:
2746.2 = (2x103) + (7x102) + (4x101) + (6x100) + (2x10-1) = 2000 + 700 + 40 +6 +0.2 = 2746.2
DATA REPRESENTATION IN COMPUTER MEMORY ------------------------------------------ Next Slide
BINARY NUMBERING SYSTEM
Define Binary numbers
Binary numbers representing number in which only digits 0 or 1.
ADDITION BINARY NUMBERS
Basic binary addition rule :
0 + 0 = 0 0 + 1 = 1 1 + 0 = 1 1 + 1 = 10
1 + 1 + 1 = 11
Example : 101 + 101 = 1010
1011 + 1011 = ?
DATA REPRESENTATION IN COMPUTER MEMORY ------------------------------------------ Next Slide
Exercise
Ex 1:
110112 + 100012 = 1011002
Ex 2:
101112 + 1112 = ________
DATA REPRESENTATION IN COMPUTER MEMORY ------------------------------------------ Next Slide
Subtraction
Four conditions in binary subtraction
0 - 0 = 0
0 - 1 = 1 borrow 1
1 - 0 = 1
1 - 1 = 0
10 - 1 = 1
If a 10 being borrow a 1, what‟s left with that 10 is a 1
DATA REPRESENTATION IN COMPUTER MEMORY ------------------------------------------ Next Slide
Ex 1:
10012 – 102 = 1112
Ex 2:
1010112 – 11112 =__________
DATA REPRESENTATION IN COMPUTER MEMORY ------------------------------------------ Next Slide
Conversions of Binary Numbers
Binary to Decimal conversions
Example : 1 1 0 1 12
24 + 23 + 22 + 21 + 20 = 16 + 8 + 2 + 1
= 2710
DATA REPRESENTATION IN COMPUTER MEMORY ------------------------------------------ Next Slide
Decimal to Binary conversions
Convert 2510 to binary number
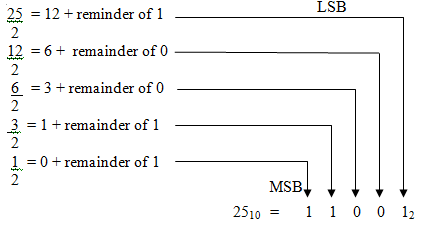
Exercise: Convert 3010 to binary number
DATA REPRESENTATION IN COMPUTER MEMORY ------------------------------------------ Next Slide
OCTAL NUMBERING SYSTEM
The octal number system has a base of eight, meaning that it has eight possible digits: 0,1,2,3,4,5,6 and 7.
The digit positions in an octal number have weights as follows :
DATA REPRESENTATION IN COMPUTER MEMORY ------------------------------------------ Next Slide
Octal number - (Subtraction - Pengurangan)
Ex:
5248 – 1678 = 3358
1678 – 248 = _________
DATA REPRESENTATION IN COMPUTER MEMORY ------------------------------------------ Next Slide
Octal –to-decimal conversion
Convert 3728 to decimal number
3728 = 3 x (82) + 7 x (81) + 2 x (80)
= (3 x 64) + (7x 8) + (2 x 1)
= 25010
DATA REPRESENTATION IN COMPUTER MEMORY ------------------------------------------ Next Slide
Decimal-to-Octal Conversion
Decimal integer can be converted to octal by using the same repeated-division method with a division factor of 8.
DATA REPRESENTATION IN COMPUTER MEMORY ------------------------------------------ Next Slide
Octal –to- Binary conversion
DATA REPRESENTATION IN COMPUTER MEMORY ------------------------------------------ Next Slide
Binary to Octal conversion
DATA REPRESENTATION IN COMPUTER MEMORY ------------------------------------------ Next Slide
HEXADECIMAL NUMBERING SYSTEM
The hexadecimal number system uses base 16.
It has 16 possible digit symbols.
It uses the digits 0 through 9 plus the letters A, B, C, D, E and F as the 16 digit symbols.
DATA REPRESENTATION IN COMPUTER MEMORY ------------------------------------------ Next Slide
Hexadecimal number - Addition (Penambahan)
DATA REPRESENTATION IN COMPUTER MEMORY ------------------------------------------ Next Slide
Hexadecimal number - Subtraction (Pengurangan)
DATA REPRESENTATION IN COMPUTER MEMORY ------------------------------------------ Next Slide
Hexadecimal-To-Decimal Conversion
A hexadecimal number can be converted to its decimal equivalent by using the fact that each hex digit position has a weight that is a power of 16.
DATA REPRESENTATION IN COMPUTER MEMORY ------------------------------------------ Next Slide
DATA REPRESENTATION IN COMPUTER MEMORY ------------------------------------------ Next Slide
DATA REPRESENTATION IN COMPUTER MEMORY ------------------------------------------ Next Slide
Decimal-To-Hexadecimal Conversion
Decimal to hex conversion can be done using repeated division by 16.
Ex: Convert 2010 to hex
DATA REPRESENTATION IN COMPUTER MEMORY ------------------------------------------ Next Slide
Hexadecimal-to-Binary Conversion
Like the octal number system, the hexadecimal number system is used primarily as a “shorthand” method for representing binary numbers.
It is a relatively simple matter to convert a hex number to binary .
Each hex digit is converted to its four-bit binary equivalent.
DATA REPRESENTATION IN COMPUTER MEMORY ------------------------------------------ Next Slide
DATA REPRESENTATION IN COMPUTER MEMORY ------------------------------------------ Next Slide
Binary-to-Hexadecimal Conversion
The binary number is grouped into groups of four bits, and each group is converted to its equivalent hex digit.
Zero are added, as needed to complete a four-bit group.
Ex:
1012 = 0101
= 516
DATA REPRESENTATION IN COMPUTER MEMORY ------------------------------------------ Next Slide
Summary
DATA REPRESENTATION IN COMPUTER MEMORY ------------------------------------------ Next Slide
2.1.4 Describe the coding system
a.Sign and magnitude b. 1‟s Complement and 2‟s Complement c. Binary Coded Decimal (BCD system) d. ASCII and EBCDIC
DATA REPRESENTATION IN COMPUTER MEMORY ------------------------------------------ Next Slide
Describe the coding system
DATA REPRESENTATION IN COMPUTER MEMORY ------------------------------------------ Next Slide
One’s Complements and Two’s Complements
One‟s Complements
One‟s complements is used in binary number.
The one‟s complement of a binary number is obtained by changing each 0 to 1 and 1 to a 0.
Only change negative number
In other words, change each bit in the number to its complement.
DATA REPRESENTATION IN COMPUTER MEMORY ------------------------------------------ Next Slide
Exp:
10011001 – original binary number
01100110 – complement each bit to form 1‟s complement
Thus, we say that the 1‟s complement of 10011001 is 01100110.
FAQs on Chapter : Data Representation In Computer Memory, PPT, Semester, Engineering - Electronics and Communication Engineering (ECE)
| 1. What is data representation in computer memory? |  |
| 2. What are the common methods used for data representation in computer memory? |  |
| 3. How does data representation in computer memory affect the performance of a computer? |  |
| 4. What is the role of data representation in computer programming? |  |
| 5. What are the challenges in data representation in computer memory? |  |















