Important Concepts: HCF & LCM | General Test Preparation for CUET UG - CUET Commerce PDF Download
| Table of contents |

|
| HCF: Highest Common Factor |

|
| Methods of Finding H.C.F |

|
| LCM: Least Common Multiple |

|
| Methods of Finding L.C.M |

|
| Important Concepts |

|
| Important Results |

|
HCF: Highest Common Factor
- Every number has some factors, but if two or more numbers taken together can have one or more common factors. Out of those common factors, the greatest among them will be the highest common divisor or highest common factor of those numbers.
- Such as 12 and 18 have 1, 2, 3 and 6 as common factors, but among them, 6 is the highest common factor. So H.C.F. of 12 and 18 is 6.

Methods of Finding H.C.F
(a) Factorisation Method- Express each number as the product of primes and take the product of the least powers of common factors to get the H.C.F.
- Follow the below-given steps to find the HCF of numbers using the prime factorisation method.
- Step 1: Write each number as a product of its prime factors. This method is called here prime factorization.
- Step 2: Now list the common factors of both the numbers
- Step 3: The product of all common prime factors is the HCF ( use the lower power of each common factor)
Example:
Evaluate the HCF of 60 and 75.
Solution:
Write each number as a product of its prime factors.22 x 3 x 5 = 60
3 x 52 = 75
The product of all common prime factors is the HCF.
The common prime factors in this example are 3 & 5.
The lowest power of 3 is 3 and 5 is 5.
So, HCF = 3 x 5 = 15
(b) Division Method
- Divide the larger number by the smaller one. Now divide the divisor by the remainder. Repeat the process of dividing the preceding divisor by the remainder last obtained, till the remainder zero is obtained.
- The last divisor is the required H.C.F.
- Steps to solve:
Step 1: Write the given numbers horizontally, in a sequence, by separating them with commas.
Step 2: Find the smallest prime number which can divide the given number. It should exactly divide the given numbers. (Write on the left side).
Step 3: Now write the quotients.
Step 4: Repeat the process, until you reach the stage, where there is no coprime number left.
Step 5: We will get the common prime factors as the factors on the left-hand side divides all the numbers exactly. The product of these common prime factors is the HCF of the given numbers. - Example:
Find highest common factor (H.C.F) of 75 and 180 by using division method.
Solution:
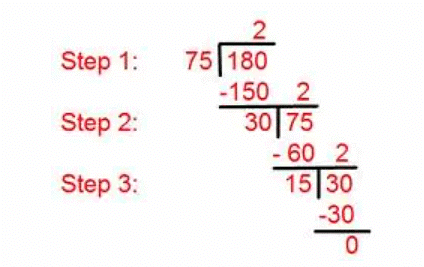
Step I:Here we need to divide 180 by 75.
[Divide the larger number by the smaller one].
Step II:The first divisor is 75 and the remainder is 30, so we need to divide 75 by 30.
[Divide the first divisor by the first remainder].
Step III: Now divide the second divisor 30 by the second remainder 15.
[Divide the second divisor by the second remainder].
Step IV: The remainder becomes 0.
Step V: Therefore, highest common factor = 15.
[The last divisor is the required highest common factor (H.C.F) of the given numbers].
LCM: Least Common Multiple
- When we write the multiples of any two or more numbers taken together, we find that they have some common multiples. Out of those common multiples, the smallest among them will be the least common multiple of those numbers.
- Such as 12 and 18 have 36, 72, 108, 144….. as common multiples, but 36 is the least among them. So, L.C.M. of 12 and 18 is 36.
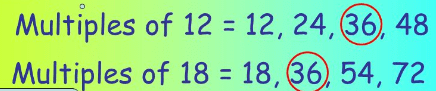
Methods of Finding L.C.M
(a) Factorisation Method
- Resolve each one of the given numbers into prime factors. Then the product of the highest power of all the factors gives the L.C.M.
Example: Find the L.C.M of 2, 4, 6, 8, 10.
- Write the numbers as the product of primes.
- 2, 22, 2× 3, 23, 2× 5
- Take the highest powers of all the primes. i.e., 23 × 3 × 5 = 120.
Example: Find the H.C.F. of 2, 4, 6, 8, 10 using the factorization method.
- For H.C.F, take the common prime factors. i.e., 2. (This is only the prime factor common in all the numbers).
(b) LCM by Division Method
- In order to find the LCM by division method, we divide the numbers by a common prime number, and these prime factors are used to calculate the LCM of those numbers. Let us understand this method using the steps given below:
- Step 1: Find a prime number which is a factor of at least one of the given numbers. Write this prime number on the left of the given numbers.
Step 2: If the prime number in step 1 is a factor of the number, then divide the number by the prime and write the quotient below it. If the prime number in step 1 is not a factor of the number, then write the number in the row below as it is. Continue the steps until 1 is left in the last row. - Example: Find the least common multiple (LCM) of 6 and 15 using the division method.
Solution: Let us find the least common multiple (LCM) of 6 and 15 using the division method using the steps given below.
Step 1: 2 is the smallest prime number and it is a factor of 6. Write 2 on the left of the two numbers. For each number in the right column, continue finding out prime numbers which are their factors.
Step 2: 2 divides 6 but it is not a factor of 15, so we write the number 15 in the row below as it is. Continue the steps until 1 is left in the last row. Then, we divide 3 and 15 by 3. This gives us 1 and 3. Now, again we write 5 on the left side and we finally get 1, 1 as the quotient in the last row.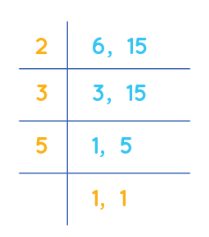
Step 3: Then we multiply these numbers on the left. The LCM is the product of all these prime numbers. LCM of 6 and 15 is, 2 × 3 × 5 = 30.
Important Concepts
(i) Product of two numbers = L.C.M. × H.C.F.
(ii) Product of n numbers = L.C.M of n numbers × Product of the HCF of each possible pair.
Or
If the HCF of all the possible pairs taken is same then we will have:
Product of n numbers = L.C.M of n numbers × (H.C.F of each pair)(n – 1)
(iii) If the ratio of numbers is a : b and H is the HCF of the numbers. Then,
LCM of the numbers = H × a × b = HCF × Product of the ratios.
(vi) H.C.F of fractions =
(vii) L.C.M. of fractions =
(viii) If HCF (a, b) = H1 and HCF (c, d) = H2, then HCF (a, b, c, d) = HCF (H1, H2).
Tip:
1. LCM is always a multiple of HCF of the numbers.
2. The numbers can be written as the multiple of HCF of them.
Important Results
Example 1: What is the greatest number which exactly divides 110, 154 and 242?
- The required number is the HCF of 110, 154 & 242.
- 110 = 2 × 5 × 11
- 154 = 2 × 7 × 11
- 242 = 2 × 11 × 11
- ∴ HCF = 2 × 11 = 22
Example 2: What is the greatest number, which when divides 3 consecutive odd numbers produces a remainder of 1.
- If x, y, z be 3 consecutive odd numbers, then the required number will be the HCF of x – 1, y – 1 and z – 1.
- Since x-1, y-1 & z-1 are 3 consecutive even integers, their HCF will be 2. So the answer is 2.
Example 3: What is the highest 3 digit number, which is exactly divisible by 3, 5, 6 and 7?
- The least no. which is exactly divisible by 3, 5, 6, & 7 is LCM (3, 5, 6, 7) = 210. So, all the multiples of 210 will be exactly divisible by 3, 5, 6 and 7.
- So, such greatest 3 digit number is 840 = (210 × 4).
Example 4: In a farewell party, some students are giving pose for photographs, if the students stand at 4 students per row, 2 students will be left if they stand 5 per row, 3 will be left and if they stand 6 per row 4 will be left. If the total number of students are greater than 100 and less than 150, how many students are there?
- If ‘N’ is the number of students, it is clear from the question that if N is divided by 4, 5, and 6, it produces a remainder of 2, 3, & 4 respectively.
- Since (4 – 2) = (5 – 3) = (6 – 4) = 2, the least possible value of N is LCM (4, 5, 6) – 2 = 60 – 2, = 58.
- But, 100 < N < 150. So, the next possible value is 58 + 60 = 118.
Example 5: There are some students in the class. Mr X brought 130 chocolates and distributed to the students equally; then he was left with some chocolates. Mr Y brought 170 chocolates and distributed equally to the students. He was also left with the same no of chocolates as MrX was left. Mr Z brought 250 chocolates, did the same thing and left with the same no of chocolates. What is the max possible no of students that were in the class?
- The question can be stated as, what is the highest number, which divides 130, 170 and 250 gives the same remainder, i.e. HCF ((170 −130),(250 −170),(250 −130)).
i.e. HCF (40, 80, 120) = 40.
|
164 videos|800 docs|1158 tests
|
FAQs on Important Concepts: HCF & LCM - General Test Preparation for CUET UG - CUET Commerce
| 1. What is the highest common factor (HCF) and how is it calculated? |  |
| 2. Can you explain the prime factorization method to find the HCF? |  |
| 3. What is the least common multiple (LCM) and how is it calculated? |  |
| 4. How can we calculate the LCM using the prime factorization method? |  |
| 5. Can you explain the relationship between HCF and LCM? |  |
















