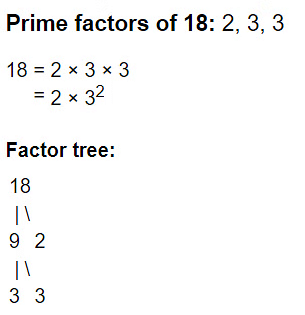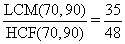HCF & LCM Important Notes | General Test Preparation for CUET UG - CUET Commerce PDF Download
HCF and LCM is another very important topic from the number system.
The concept is not just restricted to the number system but is also helpful in solving some questions from arithmetic, which is a very important topic for competitive exams.

Highest Common Factor (H.C.F.)
The H.C.F. of two or more than two numbers is the greatest number that divides each of them exactly.
- H.C.F is also called as Greatest Common Divisor (G.C.D).
- Every number has some factors, but if two or more numbers are taken together can have one or more common factors. Out of those common factors, the greatest among them will be the highest common divisor or highest common factor of those numbers.
Finding the GCD / H.C.F. - Let there be two numbers, E and R.
- Write down the prime factorization of each number.
- Find out all prime factors common to the standard forms of the numbers E and R.
- The product of the results of the previous step will be the GCD of E and R.
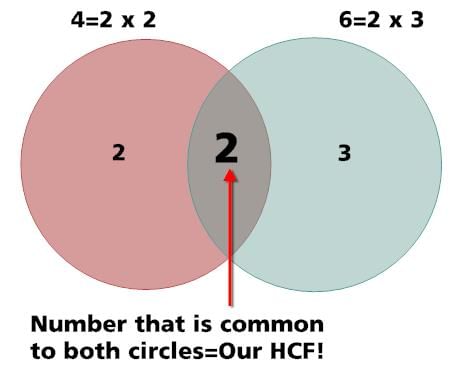
HCF of 4 and 6 via diagram is shown below:
Example: Find the GCD of 150, 210, 375.
Sol: Step 1: Writing down the Prime Factorisation of numbers
⇨ 150 = 5 X 5 X 3 X 2
⇨ 210 = 5 X 2 X 7 X 3
⇨ 375 = 5 X 5 X 5 X 3
Step 2: Writing Prime factors common to all the three numbers is 5 X 3.
Step 3: Hence, the HCF will be 5 X 3 = 15.
Methods of finding the HCF
There are basically three methods of finding out the HCF of a number
1. Factorisation Method
2. Division Method
3. Prime Factorisation
We will discuss the methods below:
1. Factorization Method
Express each number as the product of primes and take the product of the least powers of common factors to get the H.C.F.
Steps to solve:
- Step 1: Write each number as a product of its prime factors. This method is called here prime factorization.
- Step 2: Now list the common factors of both the numbers
- Step 3: The product of all common prime factors is the HCF ( use the lower power of each common factor).
Example: Evaluate the HCF of 60 and 75.
Sol: Write each number as a product of its prime factors.
22 x 3 x 5 = 60
3 x 52 = 75
The product of all common prime factors is the HCF.
The common prime factors in this example are 3 & 5.
The lowest power of 3 is 3 and 5 is 5.
So, HCF = 3 x 5 = 15
2. Division Method
- Step 1: Take the smaller number as the divisor and the larger number as a dividend.
- Step 2: Perform division. If you get the remainder as 0, then the divisor is the HCF of the given numbers.
- Step 3: If you get a remainder other than 0 then take the remainder as the new divisor and the previous divisor as the new dividend.
Example: Find out the HCF of 36 and 48.
Sol: Step I:Here we need to divide 48 by 36. ie. Dividend = 48 and Divisor = 36
[Divide the larger number by the smaller one].
Step II: Divide the 2 numbersStep III: When 12 becomes divisor, remainder becomes 0. Therefore, highest common factor = 12.
[The last divisor is the required highest common factor (H.C.F) of the given numbers].
3. Prime Factorization (Factor Tree) Method
Prime factorization is the process of breaking down a composite number into its prime factors, which are the prime numbers that multiply together to give the original number.
Steps to solve:
- Step 1: In calculating the HCF by prime factorization, we factorize the numbers into prime numbers, which are known as the prime factors.
- Step 2: Start by dividing the given numbers by 2(the first prime number), and go on dividing till you can’t divide the number any further.
- Step 3: Finally, then write the numbers as a product of the prime numbers. The product of these common factors is the highest common factor of the given numbers.
Example: Using the prime factorization method, find HCF of 18 and 90
Sol:
- Prime factorization of 18 is given below:
- Prime factorization of 90 is given below:
- There are 6 common factors of 18 and 90, that are 1, 2, 3, 6, 9, and 18. Therefore, the greatest common factor of 18 and 90 is 18.
Shortcut Method for Finding the HCF
- Identify the Numbers: Start with the set of numbers for which you want to find the HCF.
- Calculate Differences: Find the absolute differences between pairs of the numbers.
- Find the HCF of Differences: Calculate the HCF of the differences obtained. This value will also be the HCF of the original numbers.
- Verify with Original Numbers: Optionally, you can verify that this HCF divides the original numbers without leaving a remainder.
Example: Find the HCF of 36, 60, and 90
Sol: Step 1: Identify the Numbers
We want to find the HCF of the following numbers:
a = 36
b = 60
c = 90
Step 2: Calculate Differences
Now, we will find the absolute differences between pairs of these numbers:
1. Difference between 60 and 36:
|60 - 36| = 24
2. Difference between 90 and 36:
|90 - 36| = 54
3. Difference between 90 and 60.
|90 - 60| = 30So the differences we have calculated are:
24 (from 60 - 36)
54 (from 90 - 36)
30 (from 90 - 60)
Step 3: Find the HCF of Differences
Next, we calculate the HCF of the differences obtained: 24, 54, and 30.
1. Factors of each difference
- Factors of 24: 1, 2, 3, 4, 6, 8, 12, 24
- Factors of 54: 1, 2, 3, 6, 9, 18, 27, 54
- Factors of 30: 1, 2, 3, 5, 6, 10, 15, 30
2. Identify common factors:
- Common factors of 24, 54, and 30: 1, 2, 3, 6
Therefore, the HCF of 24, 54, and 30 is 6..
Least Common Multiple (L.C.M.)
LCM stands for Lowest or Least Common Multiple. The LCM of two or more numbers is the smallest positive integer that is divisible by all the given numbers.
Finding the LCM two numbers E and R
- Find the prime factorisation of the numbers E and R.
- Find out all the prime factors, which are contained in the standard forms of either of the numbers.
- Raise each of the prime factors listed above to the highest of the powers in which it appears in the standard forms of the numbers E and R.
- The product of the results of the previous step will be the LCM of E and R.
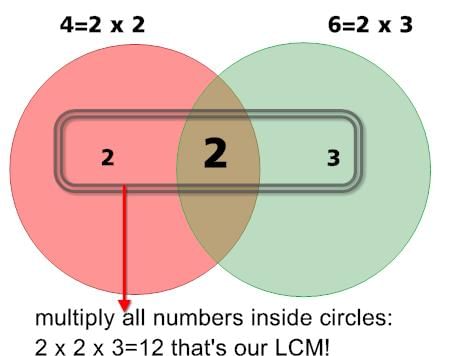
LCM of 4 and 6 via diagram is shown below:
Example: Find the LCM of 150, 210, 375.
Sol: Step 1: Writing down the standard form of numbers:
⇨ 150 = 5 × 5 × 3 × 2 = 52 × 3 × 2
⇨ 210 = 5 × 2 × 7 × 3
⇨ 375 = 5 × 5 × 5 × 3 = 53 × 3
Step 2: Write down all the prime factors: that appear at least once in any of the numbers: 5, 3, 2, 7.
Step 3: Raise each of the prime factors to their highest available power (considering each to the numbers).
The LCM = 2 × 3 × 5 × 5 × 5 × 7 = 5250.
Methods of finding the LCM
1. Prime Factorization Method
Steps involved:
- Step 1: Find the prime factors of the given numbers by repeated division method.
- Step 2: Write the numbers in their exponent form. Find the product of only those prime factors that have the highest power.
- Step 3: The product of these factors with the highest powers is the LCM of the given numbers.
Example: Find the least common multiple (LCM) of 60 and 90 using prime factorization.
Sol: Let us find the LCM of 60 and 90 using the prime factorization method.
- Step 1: The prime factorization of 60 and 90 are: 60 = 2 × 2 × 3 × 5 and 90 = 2 × 3 × 3 × 5
- Step 2: If we write these prime factors in their exponent form it will be expressed as, 60 = 22 × 31 × 51 and 90 = 21 × 32 × 51
- Step 3: Now, we will find the product of only those factors that have the highest powers among these. This will be, 22 × 32 × 51 = 4 × 9 × 5 = 180
=>LCM(60,90) = 180
2. Division Method (Shortcut Method)
Steps involved:
- Step 1: Arrange the given number in a row.
- Step 2: Divide by a number that divides exactly at least two of the given numbers and carry forward the numbers which are not divisible.
- Step 3: Repeat the above process till no two numbers are divisible by the same number except 1.
- Step 4: The product of the divisors and the undivided numbers is the required L.C.M. of the given numbers.
Example : Find the L.C.M. of 72, 240, 196.
Sol: (i) Using Prime Factorisation method:
⇨ 72 = 2 × 2 × 2 × 3 × 3 = 23 × 32
⇨ 240 = 2 × 2 × 2 × 2 × 3 × 5 = 24 × 3 × 5
⇨ 196 = 2 × 2 × 7 × 7 = 22 × 72L.C.M. of the given numbers = Product of all the prime factors of each of the given number with greatest index of common prime factors
= 24 × 32 × 5 × 72 = 16 × 9 × 5 × 49 = 35280.(ii) Using the Division method:
2 | 72, 240, 196
2 | 36, 120, 98
2 | 18, 60 , 49
3 | 9 , 30 , 493 | 3 , 10 , 49
7 | 1 , 10 , 49
7 | 1 , 10 , 1
10 | 1 , 10 , 1
| 1 , 1 , 1
L.C.M. of the given numbers:
= Product of divisors and the remaining numbers
= 2 × 2 × 2 × 3 × 3 × 10 × 49
= 35280
Co-primes: Two numbers are said to be co-primes if their H.C.F. is 1.
Relationship between HCF and LCM
Let us assume a and b are the two numbers, then the formula that expresses the relationship between their LCM and HCF is given as:
Product of Two numbers = (HCF of the two numbers) x (LCM of the two numbers) GCD (P, Q) × LCM (P, Q) = P × Q |
Note: This rule is applicable only for two numbers.
H.C.F. and L.C.M. of Decimals
In given numbers, make the same number of decimal places by annexing zeros in some numbers, if necessary. Considering these numbers without a decimal point, find H.C.F. or L.C.M. as the case may be. Now, in the result, mark off as many decimal places as are there in each of the given numbers.
- Step I: Convert each of the decimals to like decimals.
- Step II: Remove the decimal point and find the highest common factor and least common multiple as usual.
- Step III: In the answer (highest common factor /least common multiple), put the decimal point as there are a number of decimal places in the like decimals.
Example: Find the HCF and LCM of 3, 2.7, 0.09
Sol: Step-1: Write all the numbers with same number of digits after decimal point.
3.00, 2.70, 0.09Step-2: Now count the number of digits after decimal point (value is 2 for above problem) and calculate 10 power of the obtained value. Let the number be n = 102 = 100.
Step-3: Now remove the decimal point and find the LCM and HCF of the numbers.
LCM(300, 270, 9) and HCF(300, 270, 9).
- 300 = 22 x 31 x 52
270 = 21 x 33 x 51
9 = 20 x 32 x 50
LCM(300, 270, 9) = 22 x 33 x 52 = 2700
HCF(300, 270, 9) = 20 x 31 x 50 = 3
For finding the LCM and HCF, we should write the number in the power of prime numbers as written above. We should ensure that all the numbers should be written as power of prime numbers of same number. Example : 9 can be written as 32 but the other two numbers also contain 2 and 5 as primes. So we can write other two numbers as powers of 0. So 9 can be written as 20 x 32 x 50 and it won’t change the value of the number. Since we have our numbers in form of power of primes, Now the LCM is the number formed as the product of primes with its power is maximum value of the power of the same prime in given numbers.LCM = 2 power of max(2, 1, 0) x 3 power of max(1, 3, 2) x 5 power of max(2, 1, 0) = 22 x 33 x 52 = 2700 .
HCF calculation is similar but with only one change. Instead of taking max in power we take min in power.HCF = 2 power of min(2, 1, 0) x 3 power of min(1, 3, 2) x 5 power of min(2, 1, 0) = 20 x 31 x 50 = 3
Step-4: Now divide the obtained answer with our number n in step 2. The value we obtain is our required answer.
LCM(3, 2.7, 9) = 2700/100 = 27
HCF(3, 2.7, 9) = 3/100 = 0.03
Example: Find the H.C.F. and the L.C.M. of 1.20 and 22.5
Sol: Converting each of the following decimals into like decimals we get; 1.20 and 22.50
Now, expressing each of the numbers without the decimals as the product of primes we get
120 = 2 × 2 × 2 × 3 × 5 = 23 × 3 × 5
2250 = 2 × 3 × 3 × 5 × 5 × 5 = 2 × 32 × 53
Now, H.C.F. of 120 and 2250 = 2 × 3 × 5 = 30
Therefore, the H.C.F. of 1.20 and 22.5 = 0.30 (taking 2 decimal places)
L.C.M. of 120 and 2250 = 23 × 32 × 53 = 9000
Therefore, L.C.M. of 1.20 and 22.5 = 90.00 (taking 2 decimal places)
Example: Find the H.C.F. and the L.C.M. of 0.48, 0.72 and 0.108
Sol: Converting each of the following decimals into like decimals we get;
0.480, 0.720 and 0.108
Now, expressing each of the numbers without the decimals as the product of primes we get
480 = 2 × 2 × 2 × 2 × 2 × 3 × 5 = 25 × 3 × 5
720 = 2 × 2 × 2 × 2 × 3 × 3 × 5 = 24 × 32 × 5
108 = 2 × 2 × 3 × 3 × 3 = 22 × 33
Now, H.C.F. of 480, 720 and 108 = 22 × 3 = 12
Therefore, the H.C.F. of 0.48, 0.72 and 0.108 = 0.012 (taking 3 decimal places)
L.C.M. of 480, 720 and 108 = 25 × 33 × 5 = 4320
Therefore, L.C.M. of 0.48, 0.72, 0.108 = 4.32 (taking 3 decimal places)
H.C.F. and L.C.M. of Fractions
To calculate the Highest Common Factor (HCF) and Lowest Common Multiple (LCM) of fractions, find the HCF and LCM of their numerators and denominators separately.
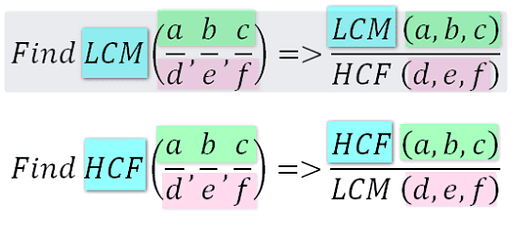
(a) HCF: To calculate the Highest Common Factor (HCF) of fractions, find the HCF of their numerators and denominators individually.
With fractions 3/6 and 5/15, the HCF of the numerators (3 and 5) is 1, and the HCF of the denominators (6 and 15) is 3. Thus, the HCF of the fractions is 1/3.
(b) LCM: To calculate the Lowest Common Multiple (LCM) of fractions, determine the LCM of their numerators and denominators separately.
The LCM of the numerators (3 and 5) is 15, and the LCM of the denominators (6 and 15) is 30. Consequently, the LCM of the fractions is 15/30, which simplifies to 1/2.
List of Properties
Property 1
- The product of LCM and HCF of any two given natural numbers is equivalent to the product of the given numbers.
LCM × HCF = Product of the Numbers. - Suppose A and B are two numbers, then.
LCM (A & B) × HCF (A & B) = A × B - For Example: If 3 and 8 are two numbers.
LCM (3,8) = 24
HCF (3,8) = 1
LCM (3,8) x HCF (3,8) = 24 x 1 = 24
Also, 3 x 8 = 24
Hence, proved.
Property 2
- HCF of co-prime numbers is 1.
- Therefore, the LCM of given co-prime numbers is equal to the product of the numbers.
LCM of Co-prime Numbers = Product Of The Numbers - For Example: Let us take two coprime numbers, such as 21 and 22.
LCM of 21 and 22 = 462
Product of 21 and 22 = 462
LCM (21, 22) = 21 x 22
Property 3
- H.C.F. and L.C.M. of Fractions
LCM of fractions = LCM of Numerators / HCF of Denominators.
HCF of fractions = HCF of Numerators / LCM of Denominators. - For Example: Let us take two fractions 4/9 and 6/21. 4 and 6 are the numerators & 9 and 12 are the denominators
LCM (4, 6) = 12
HCF (4, 6) = 2
LCM (9, 21) = 63
HCF (9, 21) = 3
Now as per the formula, we can write:
LCM (4/9, 6/21) = 12/3 = 4. Then HCF (4/9, 6/21) = 2/63
Property 4
- HCF of any two or more numbers is never greater than any of the given numbers.
- For Example: HCF of 4 and 8 is 4. Here, one number is 4 itself and another number 8 is greater than HCF (4, 8), i.e.,4.
Property 5
- LCM of any two or more numbers is never smaller than any of the given numbers.
- For Example: LCM of 4 and 8 is 8 which is not smaller to any of them.
Remainders based problems on HCF and LCM
There are generally four types of questions on finding remainders that appear in the exam; these require the concepts of HCF and LCM.
Let us understand these formulas and their working with the help of examples, one on each type.
Formula No. 1
- The greatest number that will divide A, B, and C, leaving remainders p, q, and r, respectively, is the HCF of (A-p), (B-q), and (C-r).
- Let us understand this with the help of the following example
- Example: What is the greatest number which when it divides 77, 48, and 34, leaves remainders 2, 3, and 4 respectively?
Sol: The greatest number would be the HCF of (77 – 2), (48 – 3), and (34 – 4) =HCF (75, 45 and 30), which is 15.
Formula No. 2
- The lowest number that is divisible by A, B, and C, leaving the same remainder “r” in each case is LCM of (A, B, and C) + r.
- Let us understand this with the help of the following example
- Example: What is the least number which when divided by 48, 36, and 72 leaves the remainder 3 in each case?
Sol: The least number would be LCM of (48, 36 and 72) + 3. LCM = 144.
Hence, the required number is 144 + 3 = 147
Formula No. 3
- The greatest number that will divide p, q, and r leaving the same remainder in each case, then the required number = HCF of the absolute values of (p-q), (q-r), and (r-p).
- Let us understand this with the help of the following example
- Example: Find the greatest number that will divide 65, 81, and 145 leaving the same remainder in each case.
Sol: Required number = HCF of (81-65), (145-81), and (145-65)
= HCF of 16, 64, and 80 = 16.
Formula No. 4
- If we have to find the least number which when divided by a, b, and c, leaves the same remainder p, q, and r respectively, then if it is observed that (a-p) = (b-q) = (c-r) = k (say),
- Then the required number = (LCM of a, b, and c) - k.
- Let us understand this with an example
- Example: Find the least number which when divided by 6, 7 and 9 leaves the remainder 1, 2 and 4 respectively
Sol: Here we observe that (6-1)=(7-2)=(9-4)=5.
Therefore, by applying the formula we get the required number = (LCM of 6,7 and 9) -5 = 126-5=121
HCF of the numbers in the form (am-1) and (an-1)
Direct Formula: HCF = aHCF(m,n)- 1Question: Find the HCF of 2120-1 and 250-1
Sol: HCF of (120, 50) = 10.
On applying the direct formula, we get the required HCF = 210-1.
Solved Questions
Example 1: How many pairs of integers (x, y) exist such that the product of x, y and HCF (x, y) = 1080?a. 8
b. 7
c. 9
d. 12
Ans: Option 'c ' is correct.
Sol: We need to find ordered pairs (x, y) such that xy * HCF(x, y) = 1080.
Let x = ha and y = hb where h = HCF(x, y) => HCF(a, b) = 1.
So h3(ab) = 1080 = (23)(33)(5).
We need to write 1080 as a product of a perfect cube and another number.
Four cases:
1. h = 1, ab = 1080 and b are co-prime. We gave 4 pairs of 8 ordered pairs (1, 1080), (8, 135), (27, 40) and (5, 216). (Essentially we are finding co-prime a,b such that a*b = 1080).
2. h = 2, We need to find a number of ways of writing (33) * (5) as a product of two co-prime numbers. This can be done in two ways - 1 and (33) * (5) , (33) and (5)
number of pairs = 2, number of ordered pairs = 4
3. h = 3, number of pairs = 2, number of ordered pairs = 4
4. h = 6, number of pairs = 1, number of ordered pairs = 2
Hence total pairs of (x, y) = 9, total number of ordered pairs = 18.
The pairs are (1, 1080), (8, 135), (27, 40), (5, 216), (2, 270), (10, 54), (3, 120), (24, 15) and (6, 30).Hence the answer is "9"
Example 2: Find the smallest number that leaves a remainder of 4 on division by 5, 5 on division by 6, 6 on division by 7, 7 on division by 8, and 8 on division by 9.
a. 2519
b. 5039
c. 1079
d. 979
Ans: Option 'a' is correct
Sol: When a number is divided by 8, a remainder of 7 can be thought of as a remainder of -1. This idea is very useful in a bunch of questions. So, N = 5a - 1 or N + 1 = 5a
N = 6b - 1 or N + 1 = 6b
N = 7c - 1 or N + 1 = 7c
N = 8d - 1 or N + 1 = 8d
N = 9e - 1 or N + 1 = 9e
N + 1 can be expressed as a multiple of (5, 6, 7, 8, 9)
N + 1 = 5a x 6b x 7c x 8d x 9e
Or N = (5a x 6b x 7c x 8d x 9e) - 1
Smallest value of N will be when we find the smallest common multiple of (5, 6, 7, 8, 9)
or LCM of (5, 6, 7, 8, 9)
N = LCM (5, 6, 7, 8, 9) - 1 = 2520 - 1 = 2519.
Hence the answer is "2519"
Example 3: Six bells commence tolling together and toll at intervals of 2, 4, 6, 8 10, and 12 seconds respectively. In 30 minutes, how many times do they toll together?
Sol: In this question, we have to find the least number which is divisible by 2, 4, 6, 8 10 and 12. and that number has to be the LCM of the given six numbers.
LCM (2, 4, 6, 8, 10, 12) = 120.
That means the first time all six Bells toll together is 120 seconds or 2 minutes.
Therefore, in 30 minutes they will toll =30/2=15 times.
Example 4: There are two clocks, one beats 96 times in 5 minutes and the other beats 48 times in 7 minutes. If they beat together exactly at 10 am when do they next beat together?
Sol: The time for each beat is 5/96 minutes and 7/48 minutes, or 5/96 minutes and 14/96 minutes.
Hence, they will next beat together at 35/48 minutes past 10 am.
The LCM of numerators = 70
The HCF of denominators = 90
Therefore, the LCM of the fraction =
Example 5: Rakesh and Brijesh alone can do work in 12 days and 15 days respectively. In how many days they can complete the work if they work together?
Sol: Let us assume that the work = LCM (12, 15) = 60 units.
Units of work Rakesh can do in one day = 60/12=5 units
Similarly, units of work Brijesh can do in one day = 60/15 = 4 units.
Therefore, together in one day, they can complete 5+4=9 units of work.
Hence, the total time taken by then to complete the work = 60/9 = 20/3 days.
Example 6: Sarita and Namita start running simultaneously from the same point on a circular track of length 120 meters at the speed of 10 m/s and 16 m/s respectively. In how much time they will again be together at the starting point?
Sol: Time taken by Sarita to complete one round = 120/10 = 12 sec
Similarly, the time taken by Namita to complete one round = 120/16 = 15/2 sec
Therefore, time after which both will be again at the starting point = LCM (12, 15/2) = 60 sec = 1 minute
|
201 videos|848 docs|2267 tests
|
FAQs on HCF & LCM Important Notes - General Test Preparation for CUET UG - CUET Commerce
| 1. What is the method to find the HCF of two numbers? |  |
| 2. How can I find the LCM of two numbers? |  |
| 3. What is the relationship between HCF and LCM? |  |
| 4. How do I find the HCF and LCM of decimals? |  |
| 5. Can you explain how to find the HCF and LCM of fractions? |  |