NCERT Solutions for Class 7 Maths - Simple Equations- 1
Exercise 4.1
Q1: Complete the last column of the table:
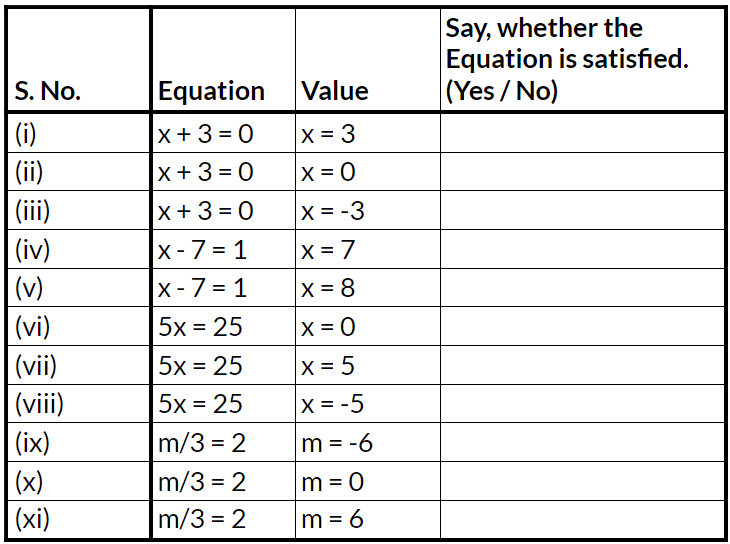
Ans:
(i) x + 3 = 0
LHS = x + 3
By substituting the value of x = 3
Then,
LHS = 3 + 3 = 6
By comparing LHS and RHS
LHS ≠ RHS
∴ No, the equation is not satisfied.
(ii) x + 3 = 0
LHS = x + 3
By substituting the value of x = 0
Then,
LHS = 0 + 3 = 3
By comparing LHS and RHS
LHS ≠ RHS
∴ No, the equation is not satisfied.
(iii) x + 3 = 0
LHS = x + 3
By substituting the value of x = – 3
Then,
LHS = – 3 + 3 = 0
By comparing LHS and RHS
LHS = RHS
∴ Yes, the equation is satisfied.
(iv) x – 7 = 1
LHS = x – 7
By substituting the value of x = 7
Then, LHS = 7 – 7 = 0
By comparing LHS and RHS
LHS ≠ RHS
∴ No, the equation is not satisfied.
(v) x – 7 = 1
LHS = x – 7
By substituting the value of x = 8
Then,
LHS = 8 – 7 = 1
By comparing LHS and RHS
LHS = RHS
∴ Yes, the equation is satisfied.
(vi) 5x = 25
LHS = 5x
By substituting the value of x = 0
Then,
LHS = 5 × 0 = 0
By comparing LHS and RHS
LHS ≠ RHS
∴ No, the equation is not satisfied.
(vii) 5x = 25
LHS = 5x
By substituting the value of x = 5
Then,
LHS = 5 × 5 = 25
By comparing LHS and RHS
LHS = RHS
∴ Yes, the equation is satisfied.
(viii) 5x = 25
LHS = 5x
By substituting the value of x = -5
Then,
LHS = 5 × (-5) = – 25
By comparing LHS and RHS
LHS ≠ RHS
∴ No, the equation is not satisfied.
(ix) m/3 = 2
LHS = m/3
By substituting the value of m = – 6
Then,
LHS = -6/3 = – 2
By comparing LHS and RHS
LHS ≠ RHS
∴ No, the equation is not satisfied.
(x) m/3 = 2
LHS = m/3
By substituting the value of m = 0
Then, LHS = 0/3 = 0
By comparing LHS and RHS
LHS ≠ RHS
∴ No, the equation is not satisfied.
(xi) m/3 = 2
LHS = m/3
By substituting the value of m = 6
Then,
LHS = 6/3 = 2
By comparing LHS and RHS
LHS = RHS
∴ Yes, the equation is satisfied.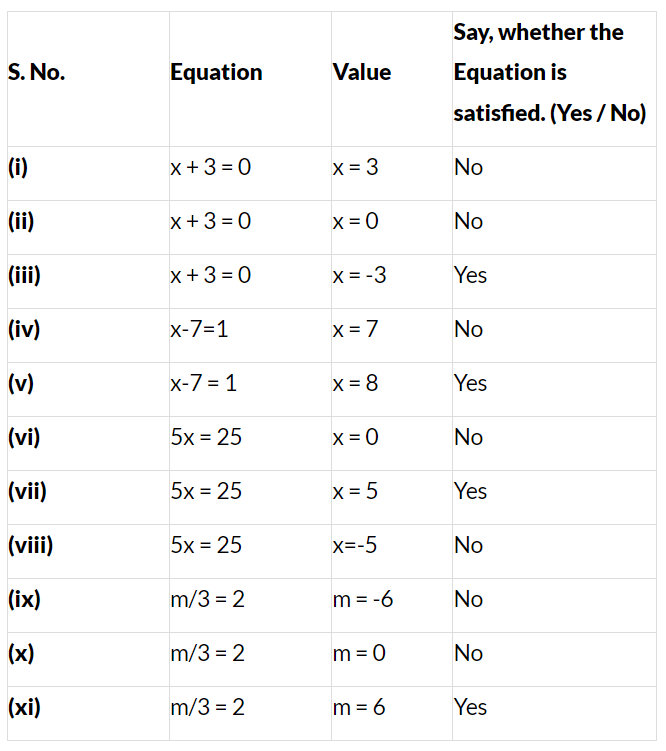
Q2: Check whether the value given in the brackets is a solution to the given equation or not:
(a) n + 5 = 19 (n = 1)
Ans: n + 5 = 19 (n = 1)
Putting n = 1 in L.H.S.,
1 + 5 = 6
∵ L.H.S. ≠ R.H.S.,
∴ n = 1 is not the solution of the given equation.
(b) 7n + 5 = 19 (n = -2)
Ans: 7n + 5 = 19 (n = -2)
Putting n = -2 in L.H.S.,
7(-2) + 5 = -14 + 5 = -9
∵ L.H.S. ≠ R.H.S.,
∴ n = -2 is not the solution of the given equation.
(c) 7n + 5 = 19 (n = 2)
Ans: 7n + 5 = 19 (n = 2)
Putting n = 2 in L.H.S.,
7(2) + 5 = 14 + 5 = 19
∵ L.H.S. = R.H.S.,
∴ n = 2 is the solution of the given equation.
(d) 4p - 3 = 13 (p = 1)
Ans: 4p - 3 = 13 (p = -4)
Putting p = 1 in L.H.S.,
4(1) - 3 = 4-3 = 1
∵ L.H.S. ≠ R.H.S.,
∴ p = 1 is not the solution of the given equation.
(e) 4p - 3 = 13 (p = -4)
Ans: 4p-3 = 13 (p = -4)
Putting p = -4 in L.H.S.,
4(-4) - 3 = -16 - 3 = -19
∵ L.H.S. ≠ R.H.S.,
∴ p = -4 is not the solution of the given equation.
(f) 4p - 3 = 13 (p = 0)
Ans: 4p - 3 = 13 (p = 0)
Putting p = 0 in L.H.S.,
4(0) - 3 = 0 - 3 = -3
∵ L.H.S. ≠ R.H.S.,
∴ p = 0 is not the solution of the given equation.
Q3: Solve the following equations by trial and error method:
(i) 5p + 2 = 17
Ans: Putting p = -3 in L.H.S.
5(-3) + 2 = -15 + 2 = -13
∵ -13 ≠ 17
Therefore, p = -3 is not the solution.
Putting p = -2 in L.H.S.
5(-2) + 2 = -10 + 2 = -8
∵ -8 ≠ 17
Therefore, p = -2 is not the solution.
Putting p = -1 in L.H.S.
5(-1) + 2= -5 + 2 =-3
∵ -3 ≠ 17
Therefore, p = -1 is not the solution.
Putting p = 0 in L.H.S.
5(0) + 2= 0 + 2 = 2
∵ 2 ≠ 17
Therefore, p = 0 is not the solution.
Putting p - 1 in L.H.S.
5(1) + 2= 5 + 2 = 7
∵ 7 ≠ 17
Therefore, p = 1 is not the solution.
Putting p = 2 in L.H.S.
5(2) + 2 = 10 + 2 = 12
∵ 12 ≠ 17
Therefore, p = 2 is not the solution.
Putting p = 3 in L.H.S.
5(3) + 2= 15 + 2 = 17
∵ 17 = 17
Therefore, p = 3 is the solution.
(ii) 3m-14 = 4
Ans: Putting m = -2 in L.H.S.
3(-2) - 14 = -6 - 14 = -20
∵ -20 ≠ 4
Therefore, m = -2 is not the solution.
Putting m = -1 in L.H.S.
3(-1) - 14 = -3 - 14 = -17
∵ -17 ≠ 4
Therefore, m =-1 is not the solution.
Putting m = 0 in L.H.S.
3(0) - 14 = 0 - 14 = -14
∵ -14 ≠ 4
Therefore, m = 0 is not the solution.
Putting m = 1 in L.H.S.
3(1) - 14 = 3 - 14 =-11
∵ -11 ≠ 4
Therefore, m = 1 is not the solution.
Putting m = 2 in L.H.S.
3(2) - 14 = 6 - 14 = -8
∵ -8 ≠ 4
Therefore, m = 2 is not the solution.
Putting m = 3 in L.H.S.
3(3) - 14 = 9 - 14 = -5
∵ -5 ≠ 4
Therefore, m = 3 is not the solution.
Putting m = 4 in L.H.S.
3(4) - 14 = 12 -14 =-2
∵ -2 ≠ 4
Therefore, m = 4 is not the solution.
Putting m = 5 in L.H.S.
3(5) - 14 = 15 - 14 = 1
∵ 1 ≠ 4
Therefore, m = 5 is not the solution.
Putting m = 6 in L.H.S.
3(6) - 14 = 18 - 14 = 4
∵ 4 = 4
Therefore, m = 6 is the solution.
Q4: Write equations for the following statements:
(i) The sum of numbers x and 4 is 9.
Ans: The above statement can be written in the equation form as,
= x + 4 = 9
(ii) 2 subtracted from y is 8.
Ans: The above statement can be written in the equation form as,
= y – 2 = 8
(iii) Ten times a is 70.
Ans: The above statement can be written in the equation form as,
= 10a = 70
(iv) The number b divided by 5 gives 6.
Ans: The above statement can be written in the equation form as,
= (b/5) = 6
(v) Three-fourth of t is 15.
Ans: The above statement can be written in the equation form as,
= ¾t = 15
(vi) Seven times m plus 7 gets you 77.
Ans: The above statement can be written in the equation form as,
Seven times m is 7m
= 7m + 7 = 77
(vii) One-fourth of a number x minus 4 gives 4.
Ans: The above statement can be written in the equation form as,
One-fourth of a number x is x/4
= x/4 – 4 = 4
(viii) If you take away 6 from 6 times y, you get 60.
Ans: The above statement can be written in the equation form as,
6 times of y is 6y
= 6y – 6 = 60
(ix) If you add 3 to one-third of z, you get 30.
Ans: The above statement can be written in the equation form as,
One-third of z is z/3
= 3 + z/3 = 30
Q5: Write the following equations in statement form:
(i) p + 4 = 15
Ans: The sum of numbers p and 4 is 15.
(ii) m - 7 = 3
Ans: 7 subtracted from m is 3.
(iii) 2m = 7
Ans: Two times m is 7.
(iv) m/5 = 3
Ans: The number m divided by 5 gives 3.
(v) 3m/5 = 6
Ans: Three-fifth of the number m is 6.
(vi) 3p + 4 = 25
Ans: Three times p plus 4 gets 25.
(vii) 4p - 2 = 18
Ans: If you take away 2 from 4 times p, you get 18.
(viii) 
Ans: If you added 2 to half is p, you get 8.
Q6: Set up an equation in the following cases:
(i) Irfan says that he has 7 marbles more than five times the marbles Parmit has. Irfan has 37 marbles. (Take m to be the number of Parmit’s marbles.)
Ans: From the question it is given that,
Number of Parmit’s marbles = m
Then,
Irfan has 7 marbles more than five times the marbles Parmit has
= 5 × Number of Parmit’s marbles + 7
= Total number of marbles Irfan having
= (5 × m) + 7 = 37
= 5m + 7 = 37
(ii) Laxmi’s father is 49 years old. He is 4 years older than three times Laxmi’s age. (Take Laxmi’s age to be y years.)
Ans: From the question it is given that,
Let Laxmi’s age to be = y years old
Then,
Lakshmi’s father is 4 years older than three times of her age
= 3 × Laxmi’s age + 4 = Age of Lakshmi’s father
= (3 × y) + 4 = 49
= 3y + 4 = 49
(iii) The teacher tells the class that the highest marks obtained by a student in her class are twice the lowest marks plus 7. The highest score is 87. (Take the lowest score to be l)
Ans: From the question it is given that,
Highest score in the class = 87
Let the lowest score be l
= 2 × Lowest score + 7
= Highest score in the class
= (2 × l) + 7 = 87
= 2l + 7 = 87
(iv) In an isosceles triangle, the vertex angle is twice either base angle. (Let the base angle be b in degrees. Remember that the sum of angles of a triangle is 180º)
Ans: From the question it is given that,
We know that the sum of angles of a triangle is 180º
Let the base angle be b
Then,
Vertex angle = 2 × base angle = 2b
= b + b + 2b = 180º
= 4b = 180º
Exercise 4.2
Q1. Give first the step you will use to separate the variable and then solve the equations:
(a) x - 1 = 0
Ans:
⇒ x - 1 + 1 = 0 + 1 [Adding 1 both sides]
⇒ x = 1
(b) x + 1 = 0
Ans:
⇒ x + 1 - 1 = 0 - 1 [Subtracting 1 both sides]
⇒ x = -1
(c) x - 1 = 5
Ans:
⇒ x - 1 + 1 = 5 + 1 [Adding 1 both sides]
⇒ x = 6
(d) x + 6 = 2
Ans:
⇒ x + 6 - 6 = 2 - 6 [Subtracting 6 both sides]
⇒ x = - 4
(e) y - 4 = -7
Ans:
⇒ y - 4 + 4 = -7 + 4 [Adding4 both sides]
⇒ y = -3
(f) y - 4 = 4
Ans:
⇒ y - 4 + 4 = 4 + 4 [Adding 4 both sides]
⇒ y = 8
(g) y + 4 = 4
Ans:
⇒ y + 4 - 4 = 4 - 4 [Subtracting 4 both sides]
⇒ y = 0
(h) y + 4 = -4
Ans:
⇒ y + 4 - 4 = - 4 - 4 [Subtracting 4 both sides]
⇒ y = -8
Ques 2: Give first the step you will use to separate the variable and then solve the equations
(a) 3l = 42
Ans:
⇒ 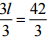 [Dividing both sides by 3]
[Dividing both sides by 3]
⇒ l = 14
(b) b/2 = 6
Ans:
⇒ 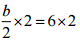 [Multiplying both sides by 3]
[Multiplying both sides by 3]
⇒ b = 12
(c) p/7 = 4
Ans:
⇒ 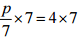 [Multiplying both sides by 7]
[Multiplying both sides by 7]
⇒ p = 28
(d) 4x = 25
Ans:
⇒  [Dividing both sides by 4]
[Dividing both sides by 4]
⇒ x = 25/4
(e) 8y = 36
Ans:
⇒ 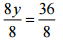 [Dividing both sides by 8]
[Dividing both sides by 8]
⇒ y = 9/2
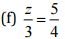
Ans:
⇒ 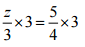 [Multiplying both sides by 3]
[Multiplying both sides by 3]
⇒ z = 15/4
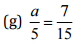
Ans:
⇒ 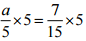 [Multiplying both sides by 5]
[Multiplying both sides by 5]
⇒ a = 7/3
(h) 20t = -10
Ans:
⇒ 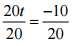 [Dividing both sides by 20]
[Dividing both sides by 20]
⇒ t = -1/2
Q3. Give first the step you will use to separate the variable and then solve the equations
(a) 3n - 2 = 46
Ans:
Step l: 3n-2+2 = 46 + 2
⇒ 3n = 48 [Adding 2 both sides]
Step II: 3n/3 = 48/3
⇒ n = 16 [Dividing both sides by 3]
(b) 5m + 7 = 17
Ans:
Step l: 5m + 7 - 7 = 17 - 7
⇒ 5m = 10 [Subtracting 7 both sides]
Step II: 5m/5 = 10/5
⇒ m = 2 [ Dividing both sides by 5]
(c) 20p/3 = 40
Ans:
Step I: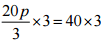 [Multiplying both sides by 3]
[Multiplying both sides by 3]
⇒ 20p = 120
Step II: 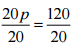 [Dividing both sides by 20]
[Dividing both sides by 20]
⇒ p = 6
(d) 3p/10 = 6
Ans:
Step I: 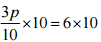 [Multiplying both sides by 10]
[Multiplying both sides by 10]
⇒ 3p = 60
Step II: 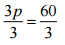 [Dividing both sides by 3]
[Dividing both sides by 3]
⇒ p = 20
Q4. Solve the following equation:
(a) 10p = 100
Ans:
⇒ 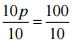 [Dividing both sides by 10]
[Dividing both sides by 10]
⇒ p = 10
(b) 10p + 10 = 100
Ans:
⇒ 10p + 10-10 = 100-10 [Subtracting both sides 10]
⇒ 10 p = 90 [Dividing both sides by 10]
[Dividing both sides by 10]
⇒ p = 9
(c) p/4 = 5
Ans:
⇒ 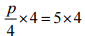 [Multiplying both sides by 4]
[Multiplying both sides by 4]
⇒ p = 20
(d) -p/3 = 5
Ans:
⇒ (-p/3)*(-3)=5*(-3) [Multiplying both sides by - 3]
⇒ p = -15
(e) 3p/4 = 6
Ans:
⇒ 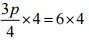 [Multiplying both sides by 4]
[Multiplying both sides by 4]
⇒ 3p = 24
⇒ 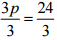 [Dividing both sides by 3]
[Dividing both sides by 3]
⇒ p = 8
(f) 3s = -9
Ans:
⇒ 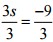 [Dividing both sides by 3]
[Dividing both sides by 3]
⇒ s = -3
(g) 3s + 12 = 0
Ans:
⇒ 3s + 12 - 12 = 0 - 12 [Subtracting both sides 10]
⇒ 3s = -12
⇒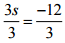 [Dividing both sides by 3]
[Dividing both sides by 3]
⇒ s = -4
(h) 3s = 0
Ans:
⇒ 3s/3 = 0/3
⇒ 3s/3 = 0/3 [Dividing both sides by 3]
⇒ s = 0
(i) 2q = 6
Ans:
⇒ 2q/2 = 6/2 [Dividing both sides by 2]
⇒ q = 3
(j) 2q - 6 = 0
Ans:
⇒ 2q - 6 + = 0 + 6 [Adding both sides 6]
⇒ 2q = 6
⇒ 2q/2 = 6/2 [Dividing both sides by 2]
⇒ q = 3
(k) 2q + 6 = 0
Ans:
⇒ 2q + 6 - 6 = 0 - 6 [Subtracting both sides 6]
⇒ 2q = -6
⇒ 2q/2 = -6/2 [Dividing both sides by 2]
⇒ q = -3
(l) 2q + 6 = 12
Ans:
⇒ 2q + - 6 = 12 - 6 [Subtracting both sides 6]
⇒ 2q = 6
⇒ 2q/2 = 6/2 [Dividing both sides by 2]
⇒ q = 3
Exercise 4.3
Q1: Set up equations and solve them to find the unknown numbers in the following cases:
(a) Add 4 to eight times a number; you get 60.
(b) One-fifth of a number minus 4 gives 3.
(c) If I take three-fourth of a number and add 3 to it, I get 21.
(d) When I subtracted 11 from twice a number, the result was 15.
(e) Munna subtracts thrice the number of notebooks he has from 50, he finds the result to be 8.
(f) Ibenhal thinks of a number. If she adds 19 to it divides the sum by 5, she will get 8.
(g) Answer thinks of a number. If he takes away 7 from 5/2 of the number, the result is 11/2
Ans: (a) Let the number be x.
According to the question, 8x + 4 = 60

(b) Let the number be y.
According to the question,

(c) Let the number be z.
According to the question, 

(d) Let the number be x.
According to the question, 2x -11 = 15
⇒ 2x = 15 +11
⇒ 2x = 26
⇒ x = 26/2
⇒ x = 13
(e) Let the number be m.
According to the question, 50-3/m = 8
⇒ -3m = 8-50
⇒ -3m = -42
⇒ m = -42/-3
⇒ m = 14
(f) Let the number be n.
According to the question, 
⇒ n + 19 = 8x5
⇒ n + 19 = 40
⇒ n = 40 - 19
⇒ n = 21
(g) Let the number be x.
According to the question, 

Q2: Solve the following:
(a) The teacher tells the class that the highest marks obtained by a student in her class are twice the lowest marks plus 7. The highest score is 87. What is the lowest score?
(b) In an isosceles triangle, the base angles are equal. The vertex angle is 40o. What are the base angles of the triangle? (Remember, the sum of three angles of a triangle is 180o. )
(c) Sachin scored twice as many runs as Rahul. Together, their runs fell two short of a double century. How many runs did each one score?
Ans: (a) Let the lowest marks be y
According to the question, 2y + 7 = 87
⇒ 2y + 7 = 87
⇒ 2y = 80
⇒ y = 80/2
⇒ y = 40
Thus, the lowest score is 40.
(b) Let the base angle of the triangle be b.
Given, a = 40°, b = c
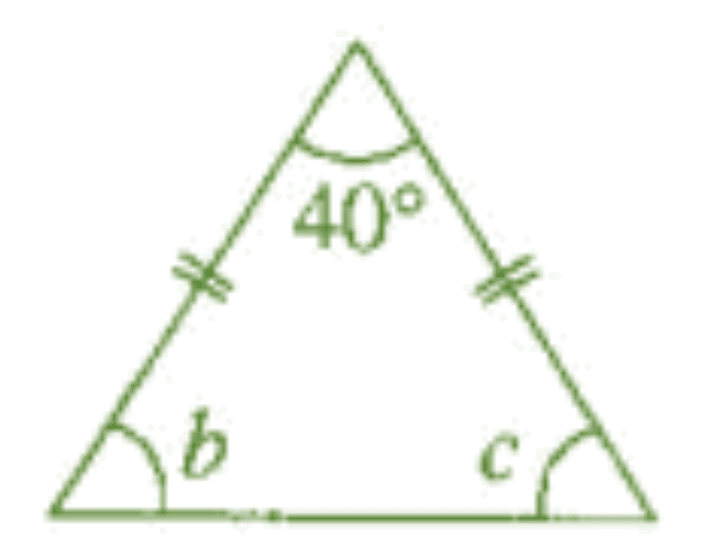
Since, a + b +c = 180° [Angle sum property of a triangle]
⇒ 40° + 6 + 6 = 180°
⇒ 40°+26 = 180°
⇒ 26 = 180°- 40°
⇒ 26 = 140°
⇒ b = 140°/2
⇒ b = 70°
Thus, the base angles of the isosceles triangle are 70° each.
(c) Let die score of Rahul be x runs and Sachin's score is 2x.
According to the question, x + 2x = 198
⇒ 3x = 198
⇒ x = 198/3
⇒ x = 66
Thus, Rahul's score = 66 runs
And Sachin's score = 2x66 = 132 runs.
Q3: Solve the following:
(i) Irfan says that he has 7 marbles more than five times the marbles Parmit has. Irfan has 37 marbles. How many marbles does Parmit have?
(ii) Laxmi’s father is 49 years old. He is 4 years older than three times Laxmi’s age. What is Laxmi’s age?
(iii) People of Sundergram planted a total of 102 trees in the village garden. Some of the trees were fruit trees. The number of non-fruit trees were two more than three times the number of fruit trees. What was the number of fruit trees planted?
Ans: (i) Let the number of marbles Parmit has be m.
According to the question, 5m + 7 = 37
⇒ 5m = 37-7
⇒ 5m = 30
⇒ m = 30/5
⇒ m = 6
Thus, Parmithas 6 marbles.
(ii) Let the age of Laxmi be y years.
Then her father's age = (3y + 4) years
According to question, 3y + 4 = 49
⇒ 3y = 49-4
⇒ 3y = 45
⇒ y = 45/3
⇒ y = 15
Thus, the age of Laxmi is 15 years.
(iii) Let the number of fruit trees be t.
Then the number of non-fruits tree = 3t + 2
According to the question, t + 3t + 2 = 102
⇒ 4t + 2 = 102
⇒ 4t = 102-2
⇒ 4t = 100
⇒ t = 100/4
⇒ t = 25
Thus, the number of fruit trees are 25.
Ques 4: Solve the following riddle:
I am a number,
Tell my identity!
Take me seven times over,
And add a fifty!
To reach a triple century,
You still need forty!
Ans: Let the number be n.
According to the question, 7n + 50 + 40 = 300
⇒ 7n + 90 = 300
⇒ 7n = 300-90
⇒ 7n = 210
⇒ n = 210/7
⇒ n = 30
Thus, the required number is 30.
|
76 videos|344 docs|39 tests
|
FAQs on NCERT Solutions for Class 7 Maths - Simple Equations- 1
| 1. What are simple equations in mathematics? |  |
| 2. How can I solve a simple equation step by step? |  |
| 3. What are some common mistakes to avoid when solving simple equations? |  |
| 4. How can I practice solving simple equations effectively? |  |
| 5. Can simple equations have more than one solution? |  |

|
Explore Courses for Class 7 exam
|

|


















