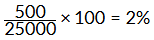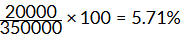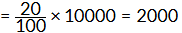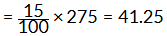NCERT Solutions for Class 7 Maths - Comparing Quantities- 1
Exercise 7.1
Q1: Convert the given fractional numbers to percent:
(a) 1/8
(b) 5/4
(c) 3/40
(d) 2/7
Ans: To convert the given fraction into percent we multiply the fraction by 100 and put the percent (%) Sign :
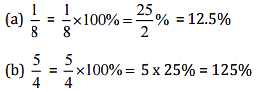

Q2: Convert the given decimal fractions to per cents:
(a) 0.65
(b) 2.1
(c) 0.02
(d) 12.35
Ans: To convert the decimals into percent, first convert them into fractions and then multiply by 100 and put a percent sign.
(a) 0.65:
0.65 can be written as 65/100.
To convert it to a percentage, we multiply it by 100.
(65/100) x 100 = 65%
Therefore, 0.65 is equal to 65%.
(b) 2.1:
2.1 remains the same.
To convert it to a percentage, we multiply it by 100.
2.1 x 100 = 210%
Therefore, 2.1 is equal to 210%.
(c) 0.02:
0.02 can be written as 2/100.
To convert it to a percentage, we multiply it by 100.
(2/100) x 100 = 2%
Therefore, 0.02 is equal to 2%.
(d) 12.35:
12.35 remains the same.
To convert it to a percentage, we multiply it by 100.
12.35 x 100 = 1235%
Therefore, 12.35 is equal to 1235%.
Q3: Estimate what part of the figures is coloured and hence find the percent which is coloured.

Ans: (i) We can observe that only 1 part is coloured out of 4 parts.
Therefore, Coloured part = 1/4
∴ Percent of coloured part = 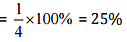

(ii) We can observe that only 3 parts is coloured out of 5 parts.
Therefore, Coloured part = 3/5
∴ Percent of coloured part 

(iii) We can observe that only 3 parts is coloured out of 8 parts.
Therefore, Coloured part = 3/8
∴ Percent of coloured part

= 37.5%
Q4: Find:
(a) 15% of 250
(b) 1% of 1 hour
(c) 20% of 2500
(d) 75% of 1 kg
Ans:
(a) 15% of 250 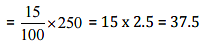
(b) We know that, 1 hour = 60 minutes = 60 x 60 seconds = 3600 seconds
1% of 1 hours = 1% of 60 minutes = 1% of (60 x 60] second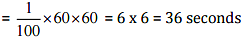
(c) 20% of Rs 2500 
(d) 75% of 1 kg = 75% of 1000 g 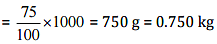
Q5: Find the whole quantity if:
(a) 5% of it is 600
(b) 12% of it is ₹1080
(c) 40% of it is 500 km
(d) 70% of it is 14 minutes
(e) 8% of it is 40 litres
Ans: Let the whole quantity be x in given questions:
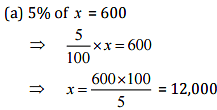
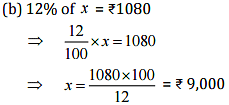
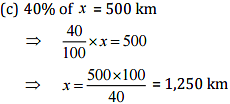
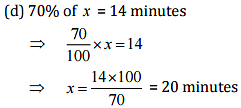
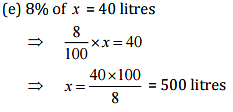
Q6: Convert given per cents to decimal fractions and also to fractions in simplest forms:
(a) 25%
(b) 150%
(c) 20%
(d) 5%
Ans: 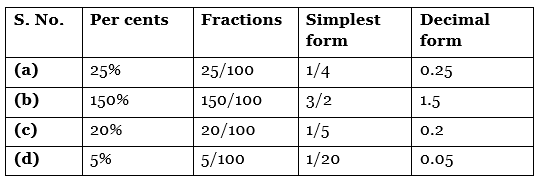
Q7: In a city, 30% are females, 40% are males and remaining are children. What percent are children?
Ans: Given Percentage of females = 30%
Percentage of males = 40%
Total percentage of females and males = 30 + 40 = 70%
Percentage of children = Total percentage - Percentage of males and females
100% - 70% = 30%
Hence, 30% are children.
Q8: Out of 15,000 voters in a constituency, 60% voted. Find the percentage of voters who did not vote. Can you now find how many actually did not vote?
Ans: Total voters = 15,000
Percentage of voted candidates = 60%
Percentage of not voted candidates = 100 - 60 = 40%
Actual candidates, who did not vote = 40% of 15000 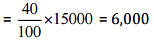
Hence, 6,000 candidates did not vote.
Q9: Meeta saves Rs 4000 from her salary. If this is 10% of her salary. What is her salary?
Ans: Let Meera's total salary be Rs x.
Now, 10% of salary = Rs 4000
⇒ 10% of x = Rs 400
⇒ (10/100) * x = Rs 4000
⇒ x = (4000 * 100)/10 = Rs 40,000
Hence, Meera's salary is Rs 40,000.
Q10: A local cricket team played 20 matches in one season. It won 25% of them. How many matches did they win?
Ans: Number of matches played by cricket team = 20
Percentage of won matches = 25%
Total matches won by them = 25% of 20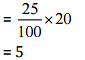
Hence, they won 5 matches.
Exercise 7.2
Q1: Tell what is the profit or loss in the following transactions. Also find profit per cent or loss per cent in each case.
(a) Gardening shears bought for ₹250 and sold for ₹325.
- Profit/Loss: ₹325 - ₹250 = ₹75 (Profit)
- Profit per cent:
(b) A refrigerator bought for ₹12,000 and sold at ₹13,500.
- Profit/Loss: ₹13,500 - ₹12,000 = ₹1,500 (Profit)
- Profit per cent:
(c) A cupboard bought for ₹2,500 and sold at ₹3,000.
- Profit/Loss: ₹3,000 - ₹2,500 = ₹500 (Profit)
- Profit per cent:
(d) A skirt bought for ₹250 and sold at ₹150.
- Profit/Loss: ₹150 - ₹250 = -₹100 (Loss)
- Loss per cent:
Q2: Convert each part of the ratio to a percentage:
(a) 3: 1
- Total parts = 3 + 1 = 4
- Percentage of first part:
- Percentage of second part: 41×100=25%
(b) 2 : 3: 5
- Total parts = 2 + 3 + 5 = 10
- Percentage of first part: 102×100=20%
- Percentage of second part:
- Percentage of third part:
(c) 1: 4
- Total parts = 1 + 4 = 5
- Percentage of first part:
- Percentage of second part:
(d) 1: 2: 5
- Total parts = 1 + 2 + 5 = 8
- Percentage of first part:
- Percentage of second part:
- Percentage of third part:
Q3: The population of a city decreased from 25,000 to 24,500. Find the percentage decrease.
- Decrease in population: 25,000 - 24,500 = 500
- Percentage decrease:

Q4: Arun bought a car for ₹3,50,000. The next year, the price went up to ₹3,70,000. What was the Percentage of price increase?
- Increase in price: ₹3,70,000 - ₹3,50,000 = ₹20,000
- Percentage increase:

Q5: I buy a T.V. for ₹10,000 and sell it at a profit of 20%. How much money do I get for it?
- Profit: 20% of ₹10,000

- Selling price: ₹10,000 + ₹2,000 = ₹12,000
Q6: Juhi sells a washing machine for ₹13,500. She loses 20% in the bargain. What was the price at which she bought it?
Ans: Loss: 20% of Cost Price (CP)
Selling Price (SP) = ₹13,500
Therefore, SP = CP - 20% of CP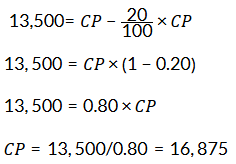
Ans: Total parts = 10 + 3 + 12 = 25
Percentage of carbon: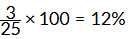
(ii) If in a stick of chalk, carbon is 3g, what is the weight of the chalk stick?
Ans: Carbon percentage: 12%
Therefore, 12% of weight of chalk = 3g
Let the weight of the chalk be W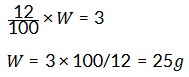
Q8: Amina buys a book for ₹275 and sells it at a loss of 15%. How much does she sell it for?
- Loss: 15% of ₹275

- Selling price: ₹275 - ₹41.25 = ₹233.75
Q9: Find the amount to be paid at the end of 3 years in each case:
(a) Principal = ₹1,200 at 12% p.a.
- Simple Interest:
- Amount: ₹1,200 + ₹432 = ₹1,632
(b) Principal = ₹7,500 at 5% p.a.
- Simple Interest:
- Amount: ₹7,500 + ₹1,125 = ₹8,625
Q10: What rate gives ₹280 as interest on a sum of ₹56,000 in 2 years?
Ans: Interest (I): ₹280
Principal (P): ₹56,000
Time (T): 2 years
Using the formula for Simple Interest:
Q11: If Meena gives an interest of ₹45 for one year at 9% rate p.a., what is the sum she has borrowed?
Ans: Interest (I): ₹45
Rate (R): 9%
Time (T): 1 year
Using the formula for Simple Interest: I = P x R x T/100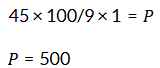
|
76 videos|344 docs|39 tests
|
FAQs on NCERT Solutions for Class 7 Maths - Comparing Quantities- 1
| 1. What are the key concepts covered in Comparing Quantities for Grade 7? |  |
| 2. How do you calculate the percentage of a quantity? |  |
| 3. What is the formula for calculating simple interest? |  |
| 4. How can we express a ratio in different forms? |  |
| 5. What is the difference between profit and loss? |  |