NCERT Solutions for Class 6 Maths - Ratio and Proportion
Exercise 12.1
Q1. There are 20 girls and 15 boys in a class.
(a) What is the ratio of number of girls to the number of boys?
(b) What is the ratio of number of girls to the total number of students in the class?
Ans:
(a) The ratio of girls to that of boys = 20/15 = 4/3 = 4:3
(b) The ratio of girls to total students = 
Q2. Out of 30 students in a class, 6 like football, 12 like cricket and remaining like tennis. Find the ratio of
(a) Number of students liking football to number of students liking tennis.
(b) Number of students liking cricket to total number of students.
Ans:
Total number of students = 30
Number of students who like football = 6
Number of students who like cricket = 12
Thus number of students who like tennis = 30 – 6 – 12 = 12
(a) The ratio of students liking football that of tennis = 6/12 = 1/2 = 1:2
(b) The ratio of students like cricket to that of total students = 12/30 = 2/5 = 2.5
Q3. See the figure and find the ratio of
(a) Number of triangles to the number of circles inside the rectangle.
(b) Number of squares to all the figures inside the rectangle.
(c) Number of circles to all the figures inside the rectangle.
Ans:
(a) Ratio of number of triangle to that of circles = 3/2 = 3:2
(b) Ratio of number of squares to all figures = 2/7 = 2:7
(c) Ratio of number of circles to all figures = 2/7 = 2:7
Q4. Distances travelled by Hamid and Akhtar in an hour are 9 km and 12 km. Find the ratio of speed of Hamid to the speed of Akhtar.
Ans: We know that, Speed = 
Speed of Hamid = 9km/1h = 9 km/h
Speed of Akhtar 12km/1h = 12 km/h
Ratio of speed of Hamid to that of speed of Akhtar 
Q5. Fill in the following blanks:
[Are these equivalent ratios?]
Ans:
Yes, these are equivalent ratios.
Q6. Find the ratio of the following:
(a) 81 to 108
(b) 98 to 63
(c) 33 km to 121 km
(d) 30 minutes to 45 minutes
Ans:
(a) Ratio of 81 to 108 
(b) Ratio of 98 to 63
(c) Ratio of 33 km to 121 km 
(d) Ratio of 30 minutes to 45 minutes
Q7. Find the ratio of the following:
(a) 30 minutes to 1.5 hours
(b) 40 cm to 1.5 m
(c) 55 paise to Rs 1
(d) 500 mL to 2 litres
Ans:
(a) 30 minutes to 1.5 hour
1.5 hours = 1.5 x 60 = 90 minutes [∵ 1 hour = 60 minutes]
Now, ratio of 30 minutes to 1.5 hour = 30 minutes: 1.5 hour
⇒ 30 minutes: 90 minutes 
(b) 40 cm to 1.5 m
1.5 m = 1.5 x 100 cm = 150 cm [∵ 1 m = 100 cm]
Now. ratio of 40 cm to 1.5 m = 40 cm : 1.5 m
(c) 55 paise to Re. 1
Rs 1 = 100 paise
Now, ratio of 55 paise to Rs1 = 55 paise : 100 paise

(d) 500 ml to 2 litters
2 litres = 2 x 1000 ml = 2000 ml [∵1 litre = 1000 ml]
Now, ratio of 500 ml to 2 litres = 500 m l : 2 litres

Q8. In a year, Seema earns Rs 1, 50, 000 and saves Rs 50, 000. Find the ratio of
(a) Money that Seema earns to the money she saves.
(b) Money that she saves to the money she spends.
Ans: Total earning = Rs 1,50,000 and Saving = Rs 50,000
∵ Money spent = Rs 1,50,000 - Rs 50,000 = Rs 1,00,000
(a) Ratio of money earned to money saved 
(b) Ratio of money saved to money spend = 
Q9. There are 102 teachers in a school of 3300 students. Find the ratio of the number of teachers to the number of students.
Ans: Ratio of number of teachers to that of students 
Q10. In a college, out of 4320 students, 2300 are girls. Find the ratio of
(a) Number of girls to the total number of students.
(b) Number of boys to the number of girls.
(c) Number of boys to the total number of students.
Ans: Total number of students in school = 4320
Number of girls = 2300
Therefore, number of boys = 4320 - 2300 = 2020
(a) Ratio of girls to total number of students
(b) Ratio of boys to that of girls
(c) Ratio of boys to total number of students
Q11. Out of 1800 students in a school, 750 opted basketball, 800 opted cricket and remaining opted table tennis. If a student can opt only one game, find the ratio of
(a) Number of students who opted basketball to the number of students who opted table tennis.
(b) Number of students who opted cricket to the number of students opting basketball.
(c) Number of students who opted basketball to the total number of students.
Ans:
Total number of students = 1800
Number of students opted basketball = 750
Number of students opted cricket = 800
Therefore, number of students opted tennis = 1800 - (750 + 800) = 250
(a) Ratio of students opted basketball to that of opted table tennis 
(b) Ratio of students opted cricket to students opted basketball 
(c) Ratio of students opted basketball to total no. of students 
Q12. Cost of a dozen pens is Rs 180 and cost of 8 ball pens is Rs 56. Find the ratio of the cost of a pen to the cost of a ball pen.
Ans: Cost of a dozen pens (12 pens) = Rs 180
∴ Cost of l pen = 180/2 = Rs 15
Cost of 8 ball pens = Rs 56
∴ Cost of l ball pen = 56/8 = Rs 7
Ratio of cost of one pen to that of one ball pen = 15/7 = 15 : 7
Q13. Consider the statement: Ratio of breadth and length of a hall is 2 : 5. Complete the following table that shows some possible breadths and lengths of the hall.
Ans: Ratio of breadth to length = 2 : 5 = 2/5
∴ Other equivalent ratios are 
Thus,
Q14. Divide 20 pens between Sheela and Sangeeta in the ratio of 3:2.
Ans: Ratio between Sheela and Sangeeta = 3 : 2
Total these terms = 3 + 2 = 5
Therefore, the part of Sheela = 3/5 of the total pens and the part of Sangeeta = 2/5 of total pens

Q15. Mother wants to divide Rs 36 between her daughters Shreya and Bhoomika in the ratio of their ages. If age of Shreya is 15 years and age of Bhoomika is 12 years, find how much Shreya and Bhoomika will get.
Ans: Ratio of the age of Shreya to that of Bhoomika
Thus, Rs 36 divide between Shreya and Bhoomika in the ratio of 5 : 4.
Shreya gets 
Bhoomika gets 
Q16. Present age of father is 42 years and that of his son is 14 years. Find the ratio of
(a) Present age of father to the present age of son.
(b) Age of the father to the age of son, when son was 12 years old.
(c) Age of father after 10 years to the age of son after 10 years.
(d) Age of father to the age of son when father was 30 years old.
Ans:
(a) Ratio of father’ s present age to that of son
(b) When son was 12 years, i.e., 2 years ago, then father was (42 - 2) = 40
Therefore, the ratio of their ages
(c) Age of father after 10 years = 42 + 10 = 52 years
Age of son after 10 years = 14 + 10 = 24 years
Therefore, ratio of their ages
(d) When father was 30 years old,
i.e., 12 years ago, then son was (14 - 12) = 2 years old
Therefore, the ratio of their ages 
Exercise 12.2
Q1. Determine if the following are in proportion.
(a) 15, 45, 40, 120
(b) 33, 121, 9, 96
(c) 24, 28, 36, 48
(d) 32, 48, 70, 210
(e) 4, 6, 8, 12
(f) 33, 44, 75, 100
Ans: (a) 
Since 15:45 = 40:120
Therefore, 15,45,40,120 are in proportion.

Since 33:121 ≠ 9:96
Therefore. 33,121, 9,96 are not in proportion.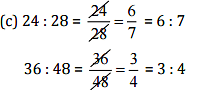
Since 24 : 28 ≠ 36 : 48
Therefore, 24, 28,36, 48 are not in proportion.
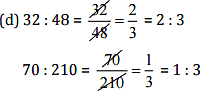
Since 32:48 ≠ 70:210
Therefore, 32,48, 70, 210 are not in proportion.
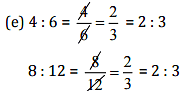
Since 4:6 = 8:12
Therefore, 4, 6, 8,12 are in proportion.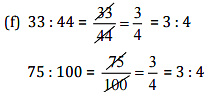
Since 33:44 = 75:100
Therefore, 33, 44, 75,100 are in proportion.
Q2. Write True (T) or False (F) against each of the following statements:
(a) 16:24::20:30
(b) 21:6::35:10
(c) 12:18::28:12
(d) 8:9::24:27
(e) 5.2:3.9::3:4
(f) 0.9:0.36::10:4
Ans:
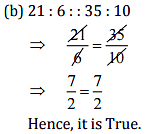
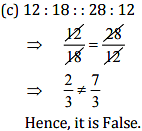
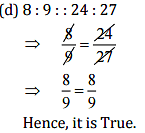

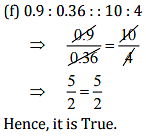
Q3. Are the following statements true?
(a) 40 persons: 200 persons = Rs 15: Rs 75
(b) 7.5 litres: 15 litres = 5 kg: 10 kg
(c) 99 kg: 45 kg = Rs 44: Rs 20
(d) 32 m: 64 m = 6 sec: 12 sec
(e) 45 km: 60 km = 12 hours: 15 hours
Ans:
(a) 40 persons: 200 persons = 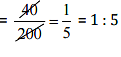

Since, 40 persons : 200 persons = Rs 15 : Rs75
Hence, the statement is true.
(b) 7.5 litres : 15 litres 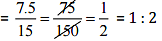

Since, 7.5 litres : 15 litres = 5 kg : 10 kg
Hence, the statement is true.
(c)
Since, 99 kg: 45 kg = Rs 44 : Rs 20
Hence, the statement is true.
Since, 32 m : 64 m = 6 sec : 12 sec
Hence, the statement is true.
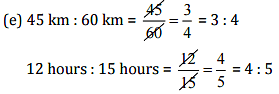
Since, 45 km : 60 km ≠ 12 hours : 15 hours
Hence, the statement is not true.
Q4. Determine if the following ratios form a proportion. Also, write the middle terms and extreme terms where the ratios form a proportion.
(a) 25 cm: 1 m and Rs 40 : Rs 160
(b) 39 litres: 65 litres and 6 bottles: 10 bottles
(c) 2 kg: 80 kg and 25 g: 625 g
(d) 200 mL: 2.5 litre and Rs 4: Rs 50
Ans:
(a) 25 cm : 1 m = 25 cm : (1 x 100) cm = 25 cm : 100 cm 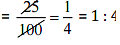

Since the ratios are equal, therefore these are in proportion.
Middle terms = 1 m, Rs 40 and Extreme terms = 25 cm, Rs 160
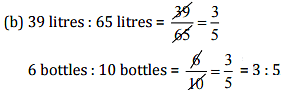
Since the ratios are equal, therefore these are in proportion.
Middle terms = 65 litres, 6 bottles and Extreme terms = 39 litres, 10 bottles
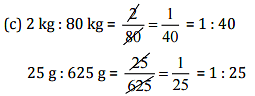
Since the ratios are not equal, therefore these are not in proportion,
(d) 200 ml :2.5 litres = 200 ml:(25000) litres = 200 ml: 2500 ml 
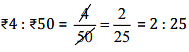
Since the ratios are equal, therefore these are in proportion.
Middle terms = 2.5 litres, Rs 4 and Extreme terms = 200 ml, Rs 50
Exercise 12.3
Q1. If the cost of 7 m of cloth is Rs 294, find the cost of 5 m of cloth.
Ans: Cost of 7 m of cloth = Rs 294
∴ Cost of 1 m of cloth 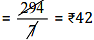
∴ Cost of 5 m of cloth = 42 x 5 = Rs 210
Thus, the cost of 5 m of cloth is Rs 210.
Q2. Ekta earns Rs 1500 in 10 days. How much will she earn in 30 days?
Ans: Earning of 10 days = Rs 1500
∴ Earning of 1 day 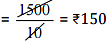
∴ Earning of 30 days = 150 x 30 = Rs 4500
Thus, the earning of 30 days is Rs 4,500.
Q3. If it has rained 276 mm in the last 3 days, how many cm of rain will fall in one full week (7 days)? Assume that the rain continues to fall at the same rate.
Ans: Rain in 3 days = 276 mm
Rain in 1 day 
∴ Rain in 7 days = 92x7 = 644 mm
As 1mm = 0.1cm
∴ 644mm = 64.4cm
Thus, the rain in 7 days is 64.4 cm.
Q4. Cost of 5 kg of wheat is Rs 30.50.
(a) What will be the cost of 8 kg of wheat?
(b) What quantity of wheat can be purchased in Rs 61?
Ans: (a) Cost of 5 kg of wheat = Rs 30.50
∴ Cost of 1 kg of wheat 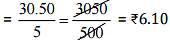
∴ Cost of 8 kg of wheat = 6.10 x 8 = Rs 48.80
(b) From Rs 30.50, quantity of wheat can be purchased = 5 kg
∴ From Rs 1, quantity of wheat can be purchased 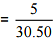
From Rs 61, quantity of wheat can be purchase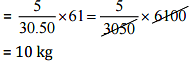
Q5. The temperature dropped 15 degree Celsius in the last 30 days. If the rate of temperature drop remains the same, how many degrees will the temperature drop in the next ten days?
Ans: Degree of temperature dropped in last 30 days = 15 degrees
Temperature drop in 1 day 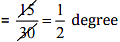
Temperature drop in next 10 days 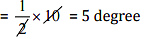
So, there will be a temperature drop of 5° Celsius in next 10 days.
Q6. Shaina pays Rs 7500 as rent for 3 months. How much does she has to pay for a whole year, if the rent per month remains same?
Ans: Rent paid for 3 months = Rs 7500
∴ Rent paid for 1 month 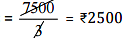
∴ Rent paid for 12 months = 2500 x 12 = Rs 30,000
Thus, the total rent for one year is Rs 30,000.
Q7. Cost of 4 dozens bananas is Rs 60. How many bananas can be purchased for Rs 12.50?
Ans: Cost of 4 dozen bananas = Rs 60
Cost of 48 bananas = Rs 60 [4 dozen = 4 x 12 = 48]
∴From Rs 60, number of bananas which can be purchased = 48
From Rs 1, number of bananas which can be purchased 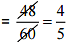
From Rs 12.50, number of bananas which can be purchased  =10 bananas
=10 bananas
Thus, 10 bananas can be purchased for Rs 12.50.
Q8. The weight of 72 books is 9 kg what is the weight of 40 such books?
Ans: The weight of 72 books = 9 kg
The weight of 1 book 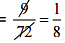
∴ The weight of 40 books 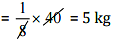
Thus, the weight of 40 books is 5 kg.
Q9. A truck requires 108 litres of diesel for covering a distance of 594 km. How much diesel will be required by the truck to cover a distance of 1650 km?
Ans: For covering 594 km, a truck will be required diesel = 108 litres
∴ For covering 1 km, a truck will be required diesel 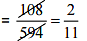
∴ For covering 1650 km, a truck will be required diesel 
Thus, 300 litres diesel is required by the truck to cover a distance of 1650 km.
Q10. Raju purchases 10 pens for Rs 150 and Manish buys 7 pens for Rs 84. Can you say who got the pen cheaper?
Ans: Raju purchase 10 pens for = Rs 150
∴ Raju purchases 1 pen for 
Manish purchases 7 pens for = Rs 84
∴ Manish purchases 1 pen for 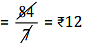
Thus, Manish got the pens cheaper.
Q11. Anish made 42 runs in 6 overs and Anup made 63 runs in 7 overs. Who made more runs per over?
Ans: Anish made in 6 overs = 42 runs
∴ Anish made in 1 overs 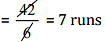
∴ Anup made in 1 overs 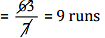
Thus, Anup made more runs per over.
|
92 videos|348 docs|54 tests
|
FAQs on NCERT Solutions for Class 6 Maths - Ratio and Proportion
| 1. What is the concept of ratio and proportion? |  |
| 2. How do you simplify ratios? |  |
| 3. How can ratios be used in real-life situations? |  |
| 4. What are the properties of ratios and proportions? |  |
| 5. How can ratios and proportions be used to solve problems? |  |

|
Explore Courses for Class 6 exam
|

|


















