NCERT Solutions for Class 8 Maths - Simple Equations- 2
Exercise 4.3
Ques 1: Solve the following equations:
Ans:
(a) 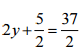
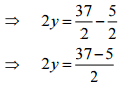
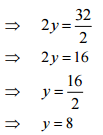
(b) 8t+28 = 10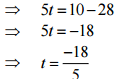
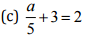
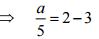
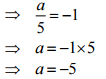
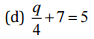
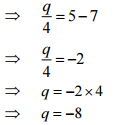
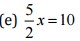
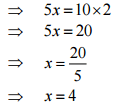
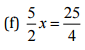
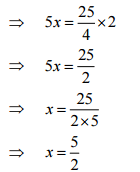
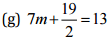
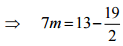
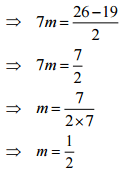
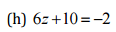
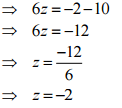
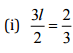
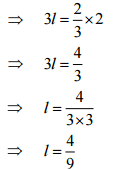
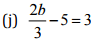
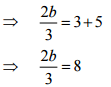
Ques 2: Solve the following equations:
(a) 2(x + 4) = 12
(b) 3(n - 5) = 21
(c) 3(n - 5) = -21
(d) 3-2(2 - y) = 7
(e) -4(2 - x) = 9
(f) 4(2 - x) = 9
(g) 4 + 5(p - 1) = 34
(h) 34 - 5(p - 1) = 4
Ans:
Ques 3: Solve the following equations:
(a) 4 = 5(p - 2)
(b) -4 = 5(p - 2)
(c) -16 = -5(2 - p)
(d) 10 = 4 + 3(t + 2)
(e) 28 = 4 + 3(t + 5)
(f) 0 = 16 + 4(m - 6)
Ans:
(a) 4 = 5 (p-2)
Ques 4: (a) Construct 3 equations starting with x = 2.
(b) Construct 3 equations starting with x = -2.
Ans: (a) 3 equations starting with x = 2.
(i) x = 2
Multiplying both sides by 10,
10* = 20
Adding 2 both sides 10x+2 = 20+2 = 10x+ 2 = 22
(ii) x = 2
Multiplying both sides by 5
5x = 10
Subtracting 3 from both sides
5x-3 = 10-3 = 5x-3 = 7
(iii) x = 2
Dividing both sides by 5
x/5 = 2/5
(b) 3 equations starting with x = -2.
(i) x = -2
Multiplying both sides by 3 3x - -6
(ii) x = -2
Multiplying both sides by 3
3x = -6
Adding 7 to both sides
3x+7 = -6+7 = 3x+7 = 1
(iii) x = -2
Multiplying both sides by 3
3x = -6
Adding 10 to both sides
3x + 10 = -6 + 10 = 3x+10 = 4
Exercise 4.4
Question 1: Set up equations and solve them to find the unknown numbers in the following cases:
(a) Add 4 to eight times a number; you get 60.
(b) One-fifth of a number minus 4 gives 3.
(c) If I take three-fourth of a number and add 3 to it, I get 21.
(d) When I subtracted 11 from twice a number, the result was 15.
(e) Munna subtracts thrice the number of notebooks he has from 50, he finds the result to be 8.
(f) Ibenhal thinks of a number. If she adds 19 to it divides the sum by 5, she will get 8.
(g) Answer thinks of a number. If he takes away 7 from 5/2 of the number, the result is 11/2
Ans: (a) Let the number be x.
According to the question, 8x + 4 = 60
(b) Let the number be y.
According to the question,
(c) Let the number be z.
According to the question,
(d) Let the number be x.
According to the question, 2x -11 = 15
⇒ 2x = 15 +11
⇒ 2x = 26
⇒ x = 26/2
⇒ x = 13
(e) Let the number be m.
According to the question, 50-3/m = 8
⇒ -3m = 8-50
⇒ -3m = -42
⇒ m = -42/-3
⇒ m = 14
(f) Let the number be n.
According to the question,
⇒ n + 19 = 8x5
⇒ n + 19 = 40
⇒ n = 40 - 19
⇒ n = 21
(g) Let the number be x.
According to the question,
Question 2: Solve the following:
(a) The teacher tells the class that the highest marks obtained by a student in her class are twice the lowest marks plus 7. The highest score is 87. What is the lowest score?
(b) In an isosceles triangle, the base angles are equal. The vertex angle is 40o. What are the base angles of the triangle? (Remember, the sum of three angles of a triangle is 180o. )
(c) Sachin scored twice as many runs as Rahul. Together, their runs fell two short of a double century. How many runs did each one score?
Ans: (a) Let the lowest marks be y
According to the question, 2y + 7 = 87
⇒ 2y + 7 = 87
⇒ 2y = 80
⇒ y = 80/2
⇒ y = 40
Thus, the lowest score is 40.
(b) Let the base angle of the triangle be b.
Given, a = 40°, b = c
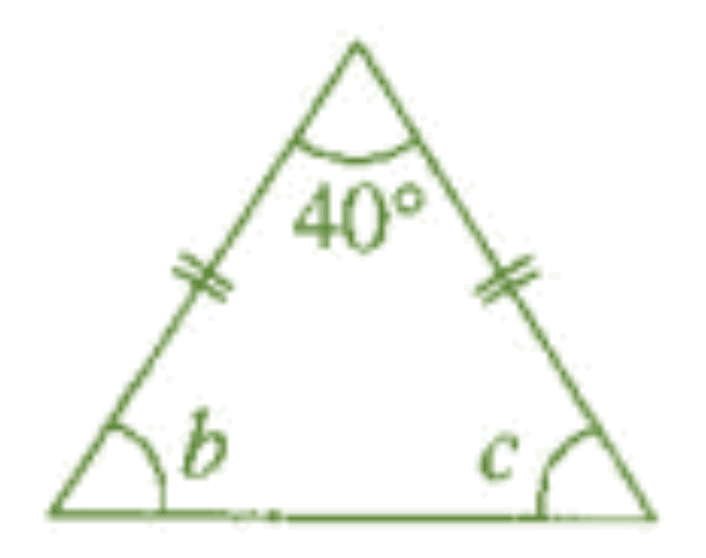
Since, a + b +c = 180° [Angle sum property of a triangle]
⇒ 40° + 6 + 6 = 180°
⇒ 40°+26 = 180°
⇒ 26 = 180°- 40°
⇒ 26 = 140°
⇒ b = 140°/2
⇒ b = 70°
Thus, the base angles of the isosceles triangle are 70° each.
(c) Let die score of Rahul be x runs and Sachin's score is 2x.
According to the question, x + 2x = 198
⇒ 3x = 198
⇒ x = 198/3
⇒ x = 66
Thus, Rahul's score = 66 runs
And Sachin's score = 2x66 = 132 runs.
Question 3: Solve the following:
(i) Irfan says that he has 7 marbles more than five times the marbles Parmit has. Irfan has 37 marbles. How many marbles does Parmit have?
(ii) Laxmi’s father is 49 years old. He is 4 years older than three times Laxmi’s age. What is Laxmi’s age?
(iii) People of Sundergram planted a total of 102 trees in the village garden. Some of the trees were fruit trees. The number of non-fruit trees were two more than three times the number of fruit trees. What was the number of fruit trees planted?
Ans: (i) Let the number of marbles Parmit has be m.
According to the question, 5m + 7 = 37
⇒ 5m = 37-7
⇒ 5m = 30
⇒ m = 30/5
⇒ m = 6
Thus, Parmithas 6 marbles.
(ii) Let the age of Laxmi be y years.
Then her father's age = (3y + 4) years
According to question, 3y + 4 = 49
⇒ 3y = 49-4
⇒ 3y = 45
⇒ y = 45/3
⇒ y = 15
Thus, the age of Laxmi is 15 years.
(iii) Let the number of fruit trees be t.
Then the number of non-fruits tree = 3t + 2
According to the question, t + 3t + 2 = 102
⇒ 4t + 2 = 102
⇒ 4t = 102-2
⇒ 4t = 100
⇒ t = 100/4
⇒ t = 25
Thus, the number of fruit trees are 25.
Ques 4: Solve the following riddle:
I am a number,
Tell my identity!
Take me seven times over,
And add a fifty!
To reach a triple century,
You still need forty!
Ans: Let the number be n.
According to the question, 7n + 50 + 40 = 300
⇒ 7n + 90 = 300
⇒ 7n = 300-90
⇒ 7n = 210
⇒ n = 210/7
⇒ n = 30
Thus, the required number is 30.
|
276 docs|155 tests
|
FAQs on NCERT Solutions for Class 8 Maths - Simple Equations- 2
| 1. What are simple equations? |  |
| 2. What is the importance of solving simple equations? |  |
| 3. What are the steps involved in solving a simple equation? |  |
| 4. Can simple equations be solved using a calculator? |  |
| 5. How can I improve my skills in solving simple equations? |  |






















