NCERT Solutions for Class 8 Maths - Factorisation- 2
Exercise 14.3
Question 1: Carry out the following divisions:
Solution:
(i)
(ii)
(iii)
(iv)
(v)
Question 2: Divide the given polynomial by the given monomial:
Solution:
(i)
(ii)
(iii)
(iv)
(v)
Question 3: Work out the following divisions:
Solution:
Question 4: Divide as directed:
Answer 4:
Question 5: Factorize the expressions and divide them as directed:
Solution: 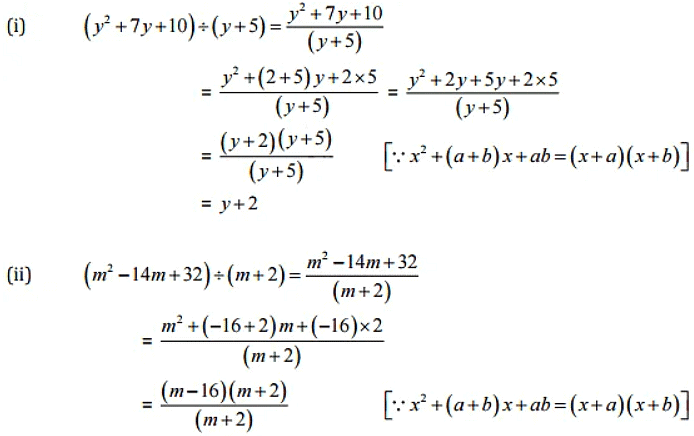
= m - 16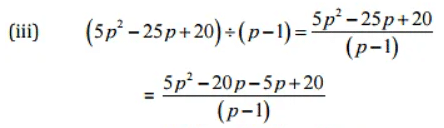
Exercise 14.4
Question: Find and correct the errors in the following mathematical statements.
1. 4(x – 5) = 4x – 5
2. x(3x + 2) = 3x2 + 2
3. 2x + 3y = 5xy
4. x + 2x + 3x = 5x
5. 5y + 2y + y – 7y = 0
6. 3x + 2x = 5x2
7. (2x)2 + 4(2x) + 7 = 2x2 + 8x + 7
8. (2x)2 + 5x = 4x + 5x = 9x2
9. (3x + 2)2 = 3x2 + 6x + 4
10. Substituting x = – 3 in
(a) x2 + 5x + 4 gives (–3)2 + 5(–3) + 4 = 9 + 2 + 4 = 15
(b) x2 – 5x + 4 gives (–3)2 – 5(–3) + 4 = 9 – 15 + 4 = – 2
(c) x2 + 5x + 4 gives (–3)2 + 5(–3) = – 9 – 15 = – 24
11. (y – 3)2 = y2 – 9
12. (z + 5)2 = z2 + 25
13. (2a + 3b)(a – b) = 2a2 – 3b2
14. (a + 4)(a + 2) = a2 + 8
15. (a – 4)(a – 2) = a2 – 8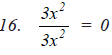
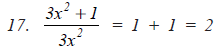
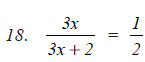
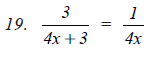
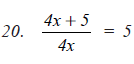
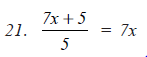
Solution:
1. 4(x – 5) = 4x – 5
The given statement is incorrect.
The correct statement is:
4(x – 5) = 4x – 20 (∵ 4 * 5 = 20)
2. x(3x + 2) = 3x2 + 2
It is an incorrect statement.
The correct statement is:
x(3x + 2) = 3x2 + 2x
3. 2x + 3y = 5xy
It is an incorrect statement.
The correct statement is:
2x + 3y = 2x + 3y
4. x + 2x + 3x = 5x
∵ 1 + 2 + 3 = 5 is an incorrect statement.
∴ The correct statement is:
x + 2x + 3x = 6x
5. 5y + 2y + y – 7y = 0
It is an incorrect statement.
∵ 5y + 2y + y = 8y and 8y – 7y = y
∴ The correct statement is
5y + 2y + y – 7y = y
6. 3x + 2x = 5x2
It is an incorrect statement.
The correct statement is:
3x + 2x = 5x
7. (2x)2 + 4(2x) + 7= 2x2 + 8x + 7
∵ (2x)2 = 4x2
∴ The given statement is incorrect.
The correct statement is:
(2x)2 + 4(2x) + 7 = 4x2 + 8x + 7
8. (2x)2 + 5x = 4x + 5x = 9x, is an incorrect statement.
∵ (2x)2 = 4x2
∴ The correct statement is:
(2x)2 + 5x = 4x2 + 5x
9. (3x + 2)2= 3x2 + 6x + 4
The given statement is incorrect.
∵ (3x + 2)2 = (3x)2 + 2(3x)(2) + (2)2
= 9x2 + 6x + 4
∴ The correct statement is:
(3x + 2)2 = 9x2 + 12x + 4
10. (a) Incorrect statement.
∵ x2 + 5x + 4 = (–3)2 + 5(–3) + 4
= 9 – 15 + 4
= (9 + 4) – 15
= 13 – 15 = –2
Thus, the correct statement is:
x2 + 5x + 4 = (–3)2 + 5(–3) + 4
= 9 – 15 + 4 = –2
(b) We have
x2 – 5x + 4 = (–3)2 – 5(–3) + 4
= 9 + 15 + 4
= 28
∴ The correct statement is
x2 – 5x + 4 at x = –3 is
(–3)2 – 5(–3) + 4 = 9 + 15 + 4 = 28
(c) ∵ x2 + 5x at x = – 3 is
(–3)2 + 5(–3) = 9 – 15 = –6
∴ The correct statement is
x2 + 5x at x = –3 is
(–3)2 + 5(–3) = 9 – 15 = –6
11. (y – 3)2 = y2 – 9
The given statement is incorrect.
∵ (y – 3)2 = y2 – 2(y)(3) + (3)2 = y2 – 6y + 9
The correct statement is
(y – 3)2 = y2 – 6y + 9
12. (z + 5)2 = z2 + 25
The given statement is incorrect.
∵ (z + 5)2 = z2 + 2(z)(5) + (5)2
= z2 + 10z + 25
∴ The correct statement is
(z + 5)2 = z2 + 10z + 25
13. (2a + 3b)(a – b) = 2a2 – 3b2
∵ (2a + 3b) (a – b) = a(2a + 3b) – b (2a – 3b)
= 2a2 + 3ab – 2ab – 3b2
= 2a2 + ab – 3b2
∴ The correct statement is
(2a + 3b)(a – b) = 2a2 + ab - 3b2
14. (a + 4)(a + 2) = a2 + 8
Since (a + 4) (a + 2) = a (a + 4) + 2 (a + 4)
= a2 + 4a + 2a + 8
= a2 + 6a + 8
15. (b – 4)(a – 2) = a2– 8
Since (a – 4)(a – 2) = a(a – 2) – 4(a – 2)
= a2 – 2a – 4a + 8
= a2 – 6a + 8
∴ The correct statement is
(a – 4)(a – 2) = a2 – 6a + 8
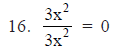 It is an incorrect statement.
It is an incorrect statement.
∵ The correct statement is
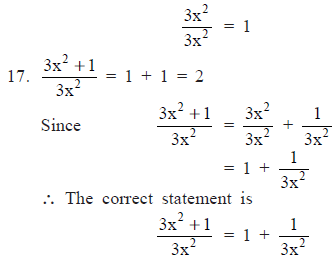

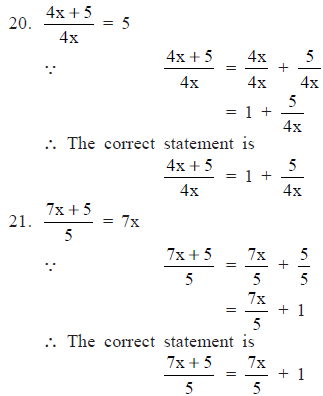
|
276 docs|155 tests
|
FAQs on NCERT Solutions for Class 8 Maths - Factorisation- 2
| 1. What is factorisation in mathematics? |  |
| 2. What are the different methods of factorisation? |  |
| 3. What is the difference between a factor and a multiple? |  |
| 4. How can factorisation be used to solve quadratic equations? |  |
| 5. What are the real-life applications of factorisation? |  |






















