Assignment - Triangles, Class 10 Mathematics PDF Download
VERY SHORT ANSWER TYPE QUESTIONS
1. In the given figure, XY||BC.
Given that AX = 3 cm, XB = 1.5 cm and BC = 6 cm.
Calculate :
(i) AY/ YC
(ii) XY.
2. D and E are points on the sides AB and AC respectively of ΔABC. For each of the following cases, state whether DE||BC:
(i) AD = 5.7 cm, BD = 9.5 cm, AE = 3.6 cm and EC = 6 cm
(ii) AB = 5.6 cm, AD = 1.4 cm, AC = 9.6 cm and EC = 2.4 cm.
(iii) AB = 11.7 cm, BD = 5.2 cm, AE = 4.4 cm and AC = 9.9 cm.
(iv) AB = 10.8 cm, BD = 4.5 cm, AC = 4.8 cm and AE = 2.8 cm.
3. In ΔABC, AD is the bisector of ∠A. If BC = 10 cm, BD = 6 cm and AC = 6 cm, find AB.
4. AB and CD are two vertical poles of height 6 m and 11 m respectively. If the distance between their feet is 12 m, find the distance between their tops.
5. ΔABC and ΔPQR are similar triangles such that area (ΔABC) = 49 cm2 and area (ΔPQR) = 25 cm2.
If AB = 5.6 cm, find the length of PQ .
6. ΔABC and ΔPQR are similar triangles such that area (ΔABC) = 28 cm2 and area (ΔPQR) = 63 cm2.
If PR = 8.4 cm, find the length of AC.
7. ΔABC ~ ΔDEF. If BC = 4 cm, EF = 5 cm and area (ΔABC) = 32 cm2, determine the area of ΔDEF.
8. The areas of two similar triangles are 48 cm2 and 75 cm2 respectively. If the altitude of the first triangle be 3.6 cm, find the corresponding altitude of the other.
9. A rectangular field is 40 m long and 30 m broad. Find the length of its diagonal.
10. A man goes 15 m due west and then 8 m due north. How far is he from the starting point?
11. A ladder 17 m long reaches the window of a building 15 m above the ground. Find the distance of the foot of the ladder from the building.
SHORT ANSWER TYPE QUESTIONS
1. In the given fig, DE||BC.
(i) If AD = 3.6 cm, AB = 9 cm and AE = 2.4 cm, find EC.
(ii) If AD / DB = 35 and AC = 5.6 cm, find AE.
(iii) If AD = x cm, DB = (x–2) cm, AE = (x+2) cm and EC = (x–1) cm, find the value of x.
2. In the given figure, BADC. Show that ΔOAB ~ ΔODC. If AB = 4 cm, CD = 3 cm, OC = 5·7 cm and OD = 3·6 cm, find OA and OB.
3. In the given figure, ∠ABC = 90° and BD AC. If AB = 5·7 cm, BD = 3·8 cm and CD =5·4 cm, find BC.
4. In the given figure, ΔABC ~ ΔPQR and AM, PN are altitudes, whereas AX and PY are medians. Prove that
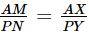
5. In the given figure, BCDE, area (ΔABC) = 25 cm2, area (trap. BCED) = 24 cm2 and DE = 14 cm. Calculate the length of BC.
6. In ΔABC, ∠C = 90°. If BC = a, AC = b and AB = c, find :
(i) c when a = 8 cm and b = 6 cm.
(ii) a when c = 25 cm and b = 7 cm
(iii) b when c = 13 cm and a = 5 cm
7. The sides of a right triangle containing the right angle are (5x) cm and (3x – 1) cm. If the area of triangle be 60 cm2, calculate the length of the sides of the triangle.
8. Find the altitude of an equilateral triangle of side 5√3 cm.
9. In the adjoining figure (not drawn to scale), PS = 4 cm, SR = 2 cm, PT = 3 cm and QT = 5cm.
(i) Show that ΔPQR ~ ΔPST. (ii) Calculate ST, if QR = 5·8 cm.
10. In the given figure, ABPQ and AC
PR. Prove that BC
QR.
11. In the given figure, AB and DE are perpendicular to BC. If AB = 9 cm, DE = 3 cm and AC = 24 cm, calculate AD.
12. In the given figure, DE ⊥ BC. If DE = 4 cm, BC = 6 cm and area (ΔADE) = 20 cm2, find the area of ΔABC.
13. A ladder 15 m long reaches a window which is 9 m above the ground on one side of the street. Keeping its foot at the same point, the ladder is turned to the other side of the street to reach a window 12 m high. Find the width of the street.
14. In the given figure, ABCD is a quadrilateral in which BC = 3 cm, AD = 13 cm, DC = 12 cm and ∠ABD = ∠BCD = 90°. Calculate the length of AB.
15. In the given figure, ∠PSR = 90°, PQ = 10 cm, QS = 6 cm and RQ = 9 cm, calculate the length of PR.
16. In a rhombus PQRS, side PQ = 17 cm and diagonal PR = 16 cm. Calculate the area of the rhombus.
17. From the given figure, find the area of trapezium ABCD.
18. In a rhombus ABCD, prove that AC2 + BD2 = 4AB2.
19. A ladder 13 m long rests against a vertical wall. If the foot of the ladder is 5 m from the foot of the wall, find the distance of the other end of the ladder from the ground.
LONG ANSWER TYPE QUESTIONS
1. In the given figure, it is given that ∠ABD = ∠CDB = ∠PQB = 90°. If AB = x units, CD = y units and PQ = z units, prove that
2. In the adjoining figure, ABCD is a parallelogram, P is a point on side BC and DP when produced meets AB produced at L. Prove that: (i) DP : PL = DC : BL (ii) DL : DP = AL : DC.
3. In the given figure, ABCD is a parallelogram, E is a point on BC and the diagonal BD intersects AE at F. Prove that: DF × FE = FB × FA.
4. In the adjoining figure, ABCD is a parallelogram in which AB = 16 cm, BC = 10 cm and L is a point on AC such that CL : LA = 2 : 3. If BL produced meets CD at M and AD produced at N, prove that:
(i) ΔCLB ~ ΔALN (ii) ΔCLM ~ ΔALB
5. In the given figure, medians AD and BE of ΔABC meet at G and DF||BE. Prove that
(i) EF = FC (ii) AG : GD = 2 : 1.
6. In the given figure, the medians BE and CF of ΔABC meet at G. Prove that:
(i) ΔGEF ~ ΔGBC and therefore, BG = 2GE. (ii) AB × AF = AE × AC.
7. In the given figure, DE⊥BC and BD = DC.
(i) Prove that DE bisects ∠ADC.
(ii) If AD = 4·5 cm, AE = 3·9 cm and DC = 7-5 cm, find CE.
(iii) Find the ratio AD : DB.
8. O is any point inside a ΔABC. The bisectors of ∠AOB, ∠BOC and ∠COA meet the sides AB, BC and CA in points D, E and F respectively. Prove that AD·BE·CF = DB·EC·FA.
9. In the figure, DE⊥BC.
(i) Prove that ΔADE and ΔABC are similar.
(ii) Given that AD = 1/2 BD, calculate DE, if BC = 4.5 cm.
10. In the adjoining figure, ABCD is a trapezium in which AB⊥DC and AB = 2 DC. Determine the ratio of the areas of ΔAOB and ΔCOD.
11. In the adjoining figure, LM is parallel to BC. AB = 6 cm, AL = 2cm and AC = 9 cm. Calculate :
(i) the length of CM.
(ii) the value of
12. In the given figure, DE||BC and DE : BC = 3 : 5. Calculate the ratio of the areas of ΔADE and the trapezium BCED.
13. In ΔABC, D and E are mid-points of AB and AC respectively. Find the ratio of the areas of ΔADE and ΔABC.
14. In a ΔPQR, L and M are two points on the base QR, such that ∠LPQ = ∠QRP and ∠RPM = ∠RQP. Prove that (i) ΔPQL ~ ΔRPM (ii) QL·RM = PL·PM (iii) PQ2 = QL·QR
15. In the adjoining figure, the medians BD and CE of a ΔABC meet at G.
Prove that:
(i) ΔEGD ~ ΔCGB
(ii) BG = 2 GD from (i) above.
16. In the adjoining figure, PQRS is a parallelogram with PQ = 15 cm and RQ = 10 cm. L is a point on RP such that RL : LP = 2 : 3. QL produced meets RS at M and PS produced at N. Find the lengths of PN and RM.
ANSWER KEY
VERY SHORT ANSWER TYPE QUESTIONS
1. (i) 2/1 (ii) 4 cm 2. (i) Yes, (ii) No, (iii) No, (iv) Yes
3. 9 cm
4. 13 m
5. PQ = 4 cm
6. AC = 5.6 cm
7. 50 cm2
8. 4.5 cm
9. 50 m
10. 17 m
11. 8 m
SHORT ANSWER TYPE QUESTIONS
1. (i) 3.6 cm, (ii) 2.1 cm, (iii) x = 4 2. OA = 4.8 cm, OB = 7.6 cm
3. 8.1 cm
5. 10 cm
6. (i) 10 cm, (ii) 24 cm, (iii) 12 cm
7. 15cm, 8 cm, 17cm
8. 7.5 cm
9. 2.9 cm
11. 16 cm
12. 45 cm2
13. 21 m
14. 4 cm
15. 17 cm
16. 240 cm2
17. 14 cm2
19. 12 m
LONG ANSWER TYPE QUESTIONS
7. (ii) 6.5 cm, (ii) 3 : 5 9. DE = 1.5 cm
10. 4 : 1
11. (i) 6 cm, (ii) 1/8
12. 9 : 16
13. 1 : 4
16. PN = 15 cm, RM = 10 cm
FAQs on Assignment - Triangles, Class 10 Mathematics
| 1. What are the different types of triangles based on their angles? |  |
| 2. Can a triangle have two right angles? |  |
| 3. How can we determine if three given sides form a triangle? |  |
| 4. What is Pythagoras' theorem and how is it used in triangles? |  |
| 5. What is the sum of the angles in a triangle? |  |















