Rankine Cycles | Mechanical Engineering SSC JE (Technical) PDF Download
| Table of contents |

|
| Steam Cycles |

|
| Internal and External Irreversibilty |

|
| Mean Temperature of Heat Addition |

|
| Regeneration |

|
| Efficiencies in a Steam Power Plant |

|
Steam Cycles
• A steam power plant continuously converts the energy stored in fossile fuels into shaft work and ultimately into electricity. The working substance is water which is some times in the liquid phase and sometimes in the vapour phase.• The fluid is undergoing a cyclic process, there will be no net change in its internal energy over the cycle (ΔdE = 0) and consequently the net energy transferred to the unit mass of the fluid as heat during the cycle must equal the net energy transfer as work from the fluid.
Δ Qnet = Δ Wnet
during cycle,
Q1 – Q2 = WT – WP
where,
Q1 = heat transferred to the working fluid kJ/kg
Q2 = heat rejected from the working fluid kJ/kg
WT = work transferred from the working fluid kJ/kg
WP = work transferred into the working fluid kJ/kg
efficiency(η)
RANKINE CYCLE
- This cycle contains four processes :
1) For steam boiler : reversible constant pressure heating process of water
2) For turbine : reversible adiabatic expansion of steam.
3) For condenser : Reversible constant pressure heat rejection
4) For pump : reversible adiabatic compression.
- When all these four processes are ideal the cycle is an ideal cycle, called a rankine cycle
Now,
For 1 kg of fluid, the steady flow energy equation to each processes :
For boiler Q1 = h1 – h4
For turbine W T = h1 – h2
For condenser Q2 = h2 – h3
For pump WP = h4 – h3
Efficiency of Rankine cycle
The pump work is small compared to the turbine work and is often neglected.
- Steam rate : The capacity of a steam plant is often expressed in terms of steam rate or specific steam consumption. It is defined as the rate of steam flow (kg/s) required to produce unit shaft output (1 kW).
Steam rate =
- Heat rate : The cycle efficiency is sometimes expressed alternatively as heat rate which is the rate of heat input (kJ/s) required to produce unit shaft output (1 kW)
Heat rate (H.R.) =
- Water is first heated sensibly in the economiser in the liquid phase at a certain pressure till it becomes saturated liquid.
QEco = h5 – h4
- In the evaporator there is phase change or boiling by absorbing the latent heat of vapourization at that pressure
QEvo = h6 – h5 = hfg
- The saturated vapour is further heated at constant pressure in the superheater to superheated state
QSH = h1 – h6
- As the pressure increases, the latent heat decreases and so the heat absorbed in the evaporator decreases and the fraction of the total heat absorbed in the superheater increases.
- For steam generators operating above the critical pressure there is no evaporator or boiling section.
However, there is a transition zone where all the liquid on being heated suddenly flashes into vapour.
Internal and External Irreversibilty
Internal Irreversibility
- Internal irreversibility of Rankine cycle is caused by fluid friction, throttling and mixing. Though the assumption of adiabatic flow in them is still valid, due to fluid friction the expansion and compression processes are not reversible and entropy of the fluid in bhoth increases.
- The isentropic Efficiency (hT) of the turbine :
- The liquid leaving the pump must be at higher pressure then turbine inlet as there is pressure drop in boiler. Pipes, valves etc. and reaches at P1 from P4 as shown below.
- The isentropic Efficiency of the Pump (h p) is
- The actual pump work would be
Thus turbine produces less work and the pump absorbs more work.
External Irrversibility
- External irreversibility of the Rankine cycle is caused due to the temperature differences between the combustion gases and the working fluid on the source side and the temperature-difference between the condensing working fluid and the condenser cooling water on the sink side.
- The point where minimum temperature difference occur are called pinch point.
Mean Temperature of Heat Addition
- In the Rankine cycle, heat is added reversibly at a constant pressure but at infinite temperatures. If Tm1 is the mean temperature of heat addition then
Heat added
Q1 = h1 – h4 = Tm1 (S1 – S4)
Heat rejected
Q2 = h2 – h3 = T2 (S1 – S4)
- Lower is the condenser Pressure, the higher will be the Efficiency of the Rankine cycle. Since it is fixed due to ambient conditions so
.
- The higher the mean temperature of heat addition the higher will be the cycle efficiency.
Effect of Superheat
(a) Mean temperature of heat addition is increased, hence efficiency is increased.
(b) The quality of steam at turbine exhaust is increased as the expansion line shifts to right. Hence performance of turbine is improved.
The maximum temperature of steam that can be used is fixed from metallurgical considerations.
- As the operating steam pressure at which heat is added in the boiler increases, the mean temperature of heat addition increases. But when the turbine inlet pressure increases the ideal expansion line of steam shifts to the left and the moisture content of steam in the later stages of the turbine is high and strike the blade with high velocity and erode their edges, as a result of which the life of the blades decreases.
- At turbine exhaust quality of steam should not fall below 88%.
Reheating of Steam
- Reheating is done to utilize higher boiler pressure while maintaining better quality of steam at turbine exhaust.
- In reheating, the expansion of steam from initial state 1 to condenser pressure is carried out in two or more steps.
- Initially the steam is expanded from state 1 to 2s in high pressure (HP) turbine, then reheated from 2s to 3 in a reheater and then expanded from 3 to 4s in low pressure (LP) turbine.
Q1 = h1 – h6s + h3 – h2s
Q2 = h4s – h5
- The net work output of the plant increases with reheat, and hence the steam rate decreases. Reheating also improves the quality at turbine exhaust.
- By increasing the number of reheats, still higher steam pressure could be used, but the mechanical stresses increases in much higher proportion than the pressure because of prevailing high temperature. In that way the maximum steam pressure gets fixed and more than two reheats results in cycle complication and increases capital cost that are not justified by improvement in the cycle efficiency.
- The optimum reheat pressure for most of the modern power plant is 0.2 to 0.25 of the initial steam pressure.
- For too low a reheat pressure the exhaust steam may even be in the-supersaturated state, which is not good for the condenser.
Regeneration
- In regeneration, the energy is exchanged internally between the expanding fluid in turbine and compressed fluid (after pump work) before heat addition.
- A well known gas cycle that uses regeneration is the stirling cycle comprising two reversible isotherms and two reversible isochors, Ideal stirling cycle has the same efficiency as the carnot cycle.
- In the Ideal regenerative cycle the condensate after leaving the pump circulates around the turbine casing so that heat is transferred from the vapour expanding in the turbine to the condensate circulating around it. It is assumed that this heat transfer process is reversible.
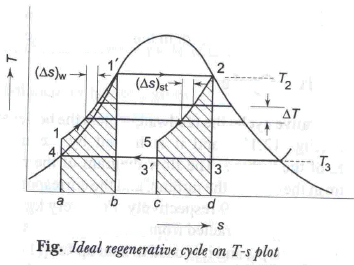
Q1 = h1 – h5 = T1 (S1 – S5)
Q2 = h2 – h3 = T2 (S2 – S3)
for reversible heat transfer
DSuniv = DSwater + DSsteam = 0
DSwater = –DSsteam
Pump work remains same as in Rankine cycle i.e.
Wp = h4s – h3
- The net work output of the ideal regenerative cycle is thus less and hence, its steam rate will be more; although it is more efficient compared to the Rankine cycle.
However the cycle is not practicable-because - Reversible heat transfer cannot be realized in finite time.
- Heat exchanger in the turbine is mechanically impracticable
- The moisture content of the steam in the turbine is high, which leads to excessive erosion of turbine blades.
Regenerative Feedwater Heating
- In practical regenerative cycle, steam is bled from the turbine and feed water is heated with it.
- In multistage regenerative cycle, more no. of feedwater pumps are used and heat added at low temperature (in economizer) is minimized.
WT = 1 (h1 – h2) + (1 – m1) (h2 – h3)
+ (1 – m1 – m2) (h3 – h4)
WP = (1 – m1 – m2) (h6 – h5) + (1 – m1)
(h8 – h7) + (h10 – h9)
Q1 = 1 (h1 – h10)
Q2 = 1 (1 – m1 – m2) (h4 – h5)
- The effects of regenerative feedwater heating for the same turbine output may be summerized as below :
-It significantly increases the cycle efficiency and reduces the heat rate.
-It increases the steam flow rate, (requiring bigger boiler).
-It reduces the steam flow to the condenser (needing smaller condenser)
-If there is no change of boiler output, the turbine output drops.
Feed Water Heaters
- These are of two types viz., open heaters and closed heaters. In an open or contact type heater, the extracted steam is allowed to mix with feed water and both leave the heater at a common temperature.
- In a closed heater, the fluids are kept separate and are not allowed to mix together.
- The condensate (saturated water at the steam extraction pressure), sometimes called the heater drip, then passes through a trap into the next lower pressure heater.
- The drip from the lowest pressure heater could similarly be trapped to the condenser, but this would be throwing away energy to the condenser cooling water.
- To avoid this waste a drip pump, pumps the drip directly into feed water stream.
- A terminal temperature difference (TTD) is defined for all closed feed water heaters as, TTD = saturation temperature of bled steam – Exit water temperature.
The value of TTD varies with pressure. - Too small a value, although good for plant efficiency, would require a larger heater.
- Too large a value would reduce the cycle efficiency.
- If the extracted steam upon condensation gets subcooled, a drain cooler may be used.
- The advantages of the open heater are simplicity lower cost, and high heat transfer capacity. The disadvantage is the necessity of a pump at each heater to handle the larger feedwater stream.
- In most steam power plants, closed heater are favoured but at least one open heater is used., Primarily for the purpose of feedwater deaeration. The open heater in such a system is called the dearator. Closed heaters are mostly horizontal.
Carnotization of Rankine Cycle
- With infinite no. of extraction stages, the irreversible process DE-the heating from condenser to boiler saturation temperature could thus be made reversible.
- The area of parallelogram CEAG which represent cycle output will be equal to the area of rectangle AFGE, which represent the output of Carnot cycle.
Regenerative feed water heating by turbine extraction is, therefore, also termed as the carnotization of the Rankine cycle. A regenerative feed heating cycle with an in finite number of feedwater heaters has thus an efficiency equal to that of carnot cycle.
- Compete carnotization of Rankine cycle is not possible with a finite number of heaters. If there is one feedwater heater used, M kg of steam is extracted from the turbine for each kg of steam entering it to heat the feed water. thermal efficiency of the cycle is
Maximum efficiency is obtained in regeneration, when the total enthalpy rise of feed water from condenser temperature to boiler temperature is equally distributed in feedwater heaters and economizers.
Super Critical Pressure Cycle
- Steam is generated in a “once through” boiler at a Pressure above the critical Point of 221.2 bar. If the Plant incorporates reheat and several stages of feedheating, here is about a 2% gain in thermal efficiency compared with the corresponding subcritical cycle. However, such an increment is gained only at the expense of increased cost and complexing of the plant.
Deaerator
- One of the feedwater heaters is a contact type open heater, known as deaerator, others being closed heaters. It is used for the purpose of deaerating the feedwater. The presence of dissolved gases like oxygen and carbon dioxide in water makes the water corrosive. These gases are removed by heating the feed water to its saturation temperature by steam extracted from turbine.
- To neutralize the effect of residual dissolved oxygen and CO2 gases in water sodium sulphite (Na2 SO3) or hydrazine (N2H4) is injected in suitable, calculated doses into the feed water at the suction of the boiler feed pump (BFP).
Efficiencies in a Steam Power Plant
- The overall efficiency of power plant is defined as
= Fuel burning rate.
- The boiler efficiency is
Ws = is the steam generation rate.
The cycle efficiency is given by
- The mechanical efficiency of the turbine will be
- The generator Efficiency of the electric alternator is
|
5 videos|103 docs|59 tests
|
FAQs on Rankine Cycles - Mechanical Engineering SSC JE (Technical)
| 1. What are the key components of a Rankine cycle in a steam power plant? |  |
| 2. How does regeneration improve the efficiency of a steam power plant? |  |
| 3. What is the significance of internal and external irreversibility in steam cycles? |  |
| 4. How does the mean temperature of heat addition impact the performance of a Rankine cycle? |  |
| 5. What are the different efficiencies that are calculated in a steam power plant using the Rankine cycle? |  |
















