Hydrostatics Force | Civil Engineering SSC JE (Technical) - Civil Engineering (CE) PDF Download
Hydrostatics Force
Pressure Force on Plane Surfaces:
- Pressure force always acts normal to plane surface.
- The center of pressure passes through centroid of the pressure diagram.
- In horizontal plane surface pressure force passes through centroid of area whereas in inclined and vertical plane surfaces pressure force passes below the centroid of the area.
- The total pressure force on plane area is F = Area × Pressure at the centroid

where,  = vertical depth of centroid of area from free liquid surface
= vertical depth of centroid of area from free liquid surface
A = Area of surface
- Depth of center of pressure from free surface is given by

where, IG = Moment of inertia about centre of gravity of the body.
- Center of pressure always lies below the centroid of the area in non-horizontal surfaces.
- The depth of center of pressure on inclined plane is given by

-Pressure Force on curved surfaces: Horizontal component of the resultant hydrostatic force 'Fx' of curved surface may be computed by projecting the surface upon a vertical plane and multiplying the projected area by the pressure at its own centre of area.
-Vertical component of force 'Fy' is equal to the weight of the liquid block lying above the curved surface upto free surface.
Resultant Force 
-Angle of line of action of resultant force with the horizontal is given by tan
-Depth of center of pressure for some vertical plane surfaces
| S.No | Surface |  |  |
| 1. | RECTANGLE | (h/2) | (2h/3) |
| 2. | TRAPEZIUM |  |  |
| 3. | TRIANGLE  | (2h/3) | (3h/4) |
| 4. | CIRCLE | (d/2) | (5d/8) |
| 5. | SEMI CIRCLE | 2D/3π | 3πD/32 |
| 6. | PARABOLA | (3h/5)
(2h/5) | (5h/7)
(4h/7) |
Archimedes principle and Force of buoyancy:
- When a body is submerged either fully or partially then it is acted upon by a force of buoyancy vertically up ward which is equal to weight of liquid displaced by the body. This force of buoyancy always acts through the centroid of liquid displaced.
- Stability of submerged bodies:If centre of buoyancy (B) and centre of gravity (G), coincide then submerged body is in neutral equilibrium & if B is above G it will be in stable equilibrium. If B is below G it will be in unstable equilibrium.

Stability of floating bodies: The stability of floating body is defined by relative position of metacentre (M) and centre of gravity (G).
-A floating body is STABLE if, when it is displaced, it returns to equilibrium.
-A floating body is UNSTABLE if, when it is displaced, it moves to a new equilibrium.
-If M lies above G (GM = +ve) then it is stable equilibrium
-If M lies below G (GM = - ve) then unstable equilibrium
-If M coincides with G (GM = 0) then neutral equilibrium
GM = (I/V) -(BG))
where GM = metacentric height.
I = moment of inertia about longitudinal axis of the plane at the level of free surface. ('I' is minimum moment of inertial of the plane.)
V = Volume of liquid displaced by the body.
BG = Distance between centroid of liquid displaced and centroid of the body.
For stable equilibrium of a circular cone floating with its apex downward having diameter 'd' and a vertical height 'h'. (The specific gravity of the cone is 'S'), The condition for stability is
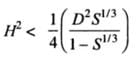
Vortex Motion : A whirling mass of fluid is called vortex flow.
(i) Forced Vortex Flow:
When a fluid is rotated about a vertical axis at constant speed, such every particle of its has the same angular velocity, motion is known as the forced vortex.Forced vortex requires constant supply of external energy/torque.
h=ω2r2/2g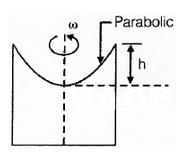
where h is height of paraboloid, and r is radius of paraboloid at top.
Volume of paraboloid = 1/2 πr2h
The surface profile of forced vortex flow is parabolic.
Example of forced vortex flow is rotating cylinder & flow inside centrifugal pump.
(ii) Free Vortex Flow:
-In this flow fluid mass rotates due to conservation of angular momentum. No external torque or energy is required. In free vortex flow Bernoulli's equation can be applied. The velocity profile is inversely proportional with the radius.
v r = constant
-The point at the centre of rotation is called singular point, where velocity approaches to infinite.
-Example of free vortex motion are whirling mass of liquid in wash basin, whirlpool in rivers etc.
|
2 videos|122 docs|55 tests
|
FAQs on Hydrostatics Force - Civil Engineering SSC JE (Technical) - Civil Engineering (CE)
| 1. What is hydrostatic force? |  |
| 2. How is hydrostatic force calculated? |  |
| 3. What is the importance of hydrostatic force? |  |
| 4. How does the shape of an object affect the hydrostatic force? |  |
| 5. Can hydrostatic force be greater than the weight of an object? |  |
|
2 videos|122 docs|55 tests
|

|
Explore Courses for Civil Engineering (CE) exam
|

|


















