Principal Stress-Strain & Theories of Failure | Civil Engineering SSC JE (Technical) - Civil Engineering (CE) PDF Download
| Table of contents |

|
| Analysis of Principal Stresses |

|
| Combined Bending & Torsion |

|
| Analysis of Principal Strains |

|
| Theories Of Elastic Failure |

|
| Solved Numericals |

|
Analysis of Principal Stresses
Principal stresses are direct normal stresses acting on mutually perpendicular planes on which shear stresses are zero. The planes which carry zero shear stresses are known as principal planes.
Case-1 : If principal stresses acting on two mutually perpendicular planes are σ1 and σ2 then, normal and shear stresses on a plane n – n which is inclined at an angle θ with the plane of σ1 are given by
Case-2 : If σx and σy are normal stresses and txy is shear stress acting on the mutually perpendicular planes then the normal and shear stresses on any plane n-n inclined at an angle θ with the plane of σx are given by
Special case-1 : If θ becomes such that ζx'y' on this plane becomes zero then this plane will be known as principal plane and the angle of principal plane is given by
The magnitude of principal stresses σ1 and σ2 are given by
σ1 or σ2 = (σx+σy)/2 ± √[(σx-σy/2)2+Τ2]
Special case-2 : The plane of maximum shear stress lies at 45° to the plane of principal stress and magnitude of ζmax is given by
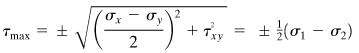
Note that planes of ζmax carry equal and alike normal stresses. The normal stress on plane of ζmax is given by
Therefore resultant stress on the plane of Тmax is
The angle of obliquity of σr with the direction of σn is given by
Special case-3 : In case of pure shear element, the principal stresses act at 45° to the plane of pure shear stress.
σ1 = + ζxy
σ2 = – ζxy ·
- Properties of Mohr’s Circle for Stress :
- Mohr’s circle is the locus on normal and shear stresses on an element with the changing angle of plane in 2 dimensional case.
The radius of Mohr’s circle is equal to maximum shear stress.
Radius,
- The centre of circle always lies on s axis and its co-ordinates are (σn, 0)
Note : Sum of normal stresses on two mutually perpendicular planes remain constant i.e.σ1 + σ2 = σx + σy = constant
- In case of pure shear element σ1 = + ζ and σ2 = – ζ therefore centre of the circle coincides with the origin,
- In case of an element inside the static fluid, ζ = 0 because principal stresses are equal and alike therefor Mohr’s circle reduces into a point
Combined Bending & Torsion
Let a shaft of diameter ‘d’ be subjected to bending moment ‘M’ and a twisting moment ‘T’ at a section. At any point in the section at radius ‘r’ and at a distance y from the neutral axis, the bending stress is given by
and shear stress is given by
Where I = Moment of inertia about its NA and Ip = Polar moment of Inertia.
- The location of the principal planes through the point is given by tan
- The principal stress es are given by
- The maximum shear stress is given by
- The position of principal planes is given by
EQUIVALENT BENDING MOMENT & EQUIVALENT TORQUE
- Let ‘Me’ be the equivalent bending moment which acts alone producing the maximum tensi l e stress equal to σ1, as produced by M and T.
Therefore
- Let ‘Te’ be the equivalent torque, which acts alone producing the same maximum shearing stress tmax as produced by M and T.
Analysis of Principal Strains
- Case-1 : If ε1 and ε2 are principal strains in two mutual perpendicular directions in plane stress problem then principal stresses are given by
- If ε1 and ε2 are principal strains in x and y directions respectively, then normal and shear strain in any other direction x' are given by
- If εx, εy and φxy are normal and shear strain in x – y plane the normal and shear strain in x' – y' plane are given by
Special case : If φx'y' = 0 then magnitude of principal strains and their plane are given by
- Properties of Mohr’s circle for strain
The radius of Mohr’s circle is half of maximum shear strain i.e.
Therefore Diameter of Mohr’s circle,
Static Loading & Dynamic Loading
When load is increased gradually from zero to P, it is called static loading. Under static loading the normal stress ’σ’ developed due to load P is given by
σ = (P/A)
When load is applied suddenly, then the normal stress ‘σ’ due to load P is given by
σ = (2P/A)
Hence, maximum stress intensity due to suddenly applied load is twice the stress intensity produced by the load of the same magnitude applied gradually.
Theories Of Elastic Failure
- Function of theories of elastic failure is to predict the behaviour of materials in simple tensile test when elastic failure will occur under any condition of applied stress.
- Maximum principal stress theory (Rankine) This assumes that max. principal stress in the complex system reaches the elastic limit stress in simple tension and failure occurs when σ1 = σy for tension Failure can occur in compression when least principal stress (σ3) reaches the elastic limit stress in compression i.e. σ3 = σy for compression
- It is well suited for brittle materials.
Failure envelope occurs when
(a) σ1 or σ2 = σyt or σyc
(ii) σ3 = 0
- Max shear stress theory (Guest - Tresca) This assumes that max shear stress in the complex stress system becomes equal to that at the yield point in simple tensile test.
- This theory holds good for ductile materials. For like stresses in Ist and IIIrd quadrant σ1 = σy or σ2 = σy
- For unlike stresses in IInd or IVth quadrant
Note : Aluminium alloys & certain steels are not governed by the Guest theory.
- Max principal strain theory (Saint Venant) This assumes that failure occurs when max. strain in the complex stress system equals that at the yield point in the tensile test (σ1 – µσ2 – µσ3) = σy
Failure should occur at higher load because the Poisson's ratio reduces the effect in perpendicular directions
RHOMBUS
- Maximum strain energy theory (Haigue)or Total strain Energy Theory : -This assumes that failure occur when total strain energy in the complex system is equal to that at the yield point in tensile test.
It is fairly good for ductile materials.
ELLIPSE
- Maximum shear strain energy theory or distortion energy theory (Mises-Henky Theory).
The properties are similar in tension and compression
ELLIPSE
- Failure of most ductile materials is governed by the distortion energy criterion or Von mises theory.
σ1 = σ2 = σ3; cylinder
σ1 = σ2 and σ3 = 0; ellipse · - Factor of safety = Tensile strength / Allowable working stress
Solved Numericals
Example 1: According to the maximum normal stress theory, the diameter of circular shaft subjected to bending moment M and torque T is
(where σy is the yield stress in the uniaxial tensile test and N is the factor of safety)
(a)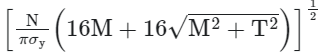
(b)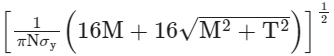
(c)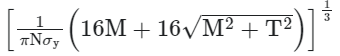
(d)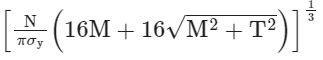
Ans: (d)
Solution:
As per this theory, for no failure maximum principal stress should be less than yield stress under uniaxial loading.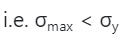
For design, 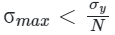
Where N is the factor of safety
Circular cross-section when subjected to pure bending develops normal stress which is given by: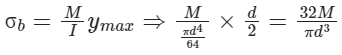
Circular cross-section when subjected to pure twisting moment develops shear stress which is given by: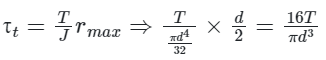
The combined effect of bending and torsion produces principal stress which is given by: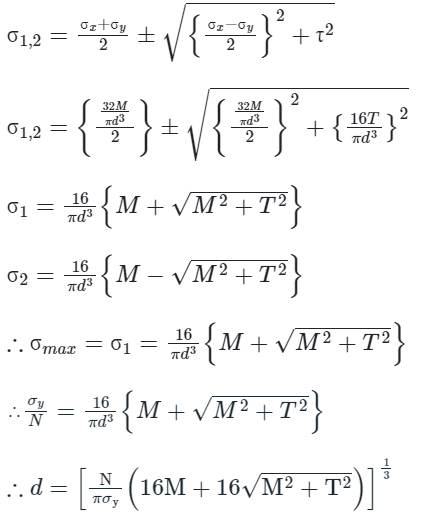
Example 2: The yield strength of bolt material is 300 MPa and factor of safety is 2.5. What is the maximum principal stress using maximum principal stress theory ?
(a) 750 MPa
(b) 120 MPa
(c) 27.38 MPa
(d) 10.95 MPa
Ans: (b)
Solution:
Maximum principal stress theory (Rankine’s theory)
According to this theory, failure happens under a state of complex stress, when the value of maximum principal stress is equal to that of yield point stress as found in a simple tensile test.
For the design criterion, the maximum principal stress (σ1) must not exceed the working stress ‘σy’ for the material.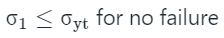
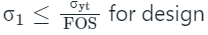
Calculation:
Given:
σyt = 300 MPa, FOS = 2.5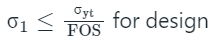
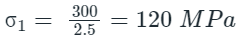
Example 3: In metal forming operation when the material has just started yielding, the principle stresses are σ1 = +180 MPa, σ2 = -100 MPa, σ3 = 0. Following the Von Mises criterion, the yield stress is ________ MPa.
Ans: 245 - 246
Solution:
According to von Mises theory, for yielding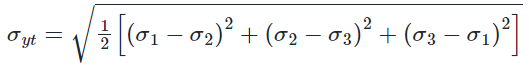
Calculation:
Given:
σ1 = +180 MPa, σ2 = -100 MPa, σ3 = 0
Yield stress is:
σyt = 245.76 MPa
|
2 videos|133 docs|55 tests
|
FAQs on Principal Stress-Strain & Theories of Failure - Civil Engineering SSC JE (Technical) - Civil Engineering (CE)
| 1. What is the significance of analyzing principal stresses in combined bending and torsion? |  |
| 2. How do engineers analyze principal strains in structural components? |  |
| 3. What are the theories of elastic failure commonly used in civil engineering? |  |
| 4. Can you provide an example of a numerical problem involving principal stress-strain analysis? |  |
| 5. What are some common challenges faced by civil engineers when analyzing principal stresses and strains in structural components? |  |
















