Gravitation & Related Terms | Physics Class 11 - NEET PDF Download
Introduction
- Newton observed that an object, an apple, when released near the earth surface is accelerated towards the earth. As acceleration is caused by an unbalanced force, there must be a force pulling objects towards the earth.
- If someone throws a projectile with some initial velocity, then instead of that object moving off into space in a straight line, it is continuously acted on by a force pulling it back to earth. If we throw the projectile with greater velocity then the path of projectile would be different as well and its range is also increased with initial velocity.
 Fig: Difference between gravitation and gravity
Fig: Difference between gravitation and gravity
- If the projection velocity is further increased until at some initial velocity, the body would not hit the earth at all but would go right around it in an orbit. But at any point along its path the projectile would still have a force acting on it pulling it toward the surface of earth.
- Newton was led to the conclusion that the same force that causes the apple to fall to the earth also causes the moon to be pulled to the earth. Thus the moon moves in its orbit about the earth because it is pulled toward the earth.
- But if there is a force between the moon and the earth, why not a force between the sun and the earth or why not a force between the sun and the other planets?
- Newton proposed that the same force, named gravitational force which acts on objects near the earth surface also acts on all the heavenly bodies.
- He proposed that there was a force of gravitation between each and every mass in the universe.
Newton’s Law Of Universal Gravitation
Newton’s Law of Universal Gravitation states that every particle attracts every other particle in the universe with a force that is directly proportional to the product of the masses and inversely proportional to the square of the distance between them.
The universal gravitation equation thus takes the form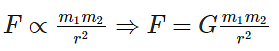
 Gravitation Equation
Gravitation Equation
where F is the gravitational force between bodies, m1 is the mass of one of the objects, m2 is the mass of the second object, r is the distance between the centers of two objects, and G is the universal gravitational constant.
The constant proportionality (G) in the above equation is known as the universal gravitation constant. Henry Cavendish experimentally determined the precise value of G.
The value of G is found to be G = 6.673 x 10-11 N m2/kg2.
[Question: 906079]
Properties of Gravitational Force
- The gravitational force is a conservative force, operating along the central axis connecting two objects, which qualifies it as a central force.
- It remains unaffected by the medium between the two objects, as well as the characteristics and dimensions of the objects themselves.
- This force complies with Newton's third law of motion, forming an action-reaction pair, and it remains unaltered by the presence or absence of other bodies in the surrounding environment.
Gravitation Equation Vector Form
The universal gravitation equation is represented in vector form as follows: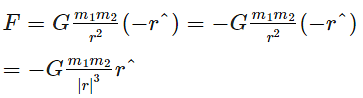
where G is the gravitational constant and r is the unit vector from m1 to m2. The figure below shows the gravitational force on m1 due to m2 along with r where the vector r is (r2–r1). 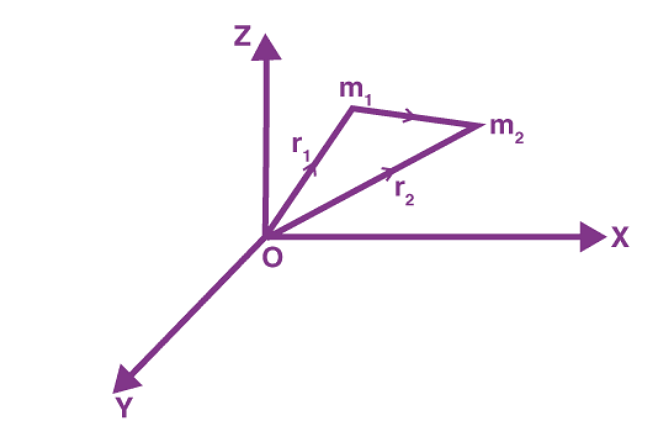
If we have a collection of point masses, the force on any one of them is the vector sum of the gravitational forces exerted by the other point masses: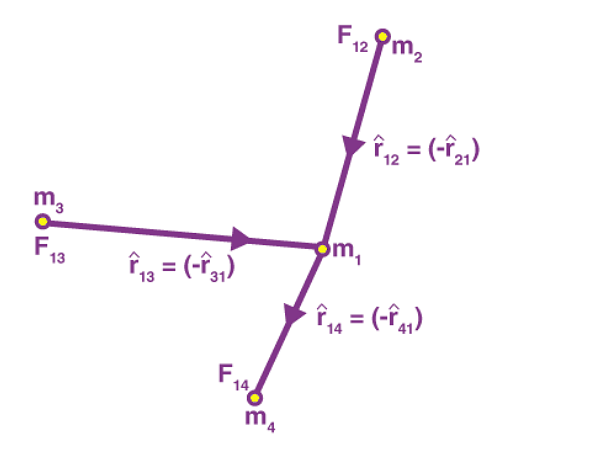
The gravitational force on point mass m1 is the vector sum of the gravitational forces exerted by m2, m3 and m4. Therefore, the total force on m1 is given by: 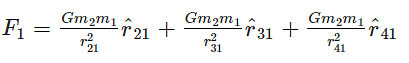
Example 1: Calculate the gravitational force of attraction between the Earth and a 70 kg man standing at sea level, a distance of 6.38 x 106 m from the Earth’s center.
Solution:
Given,
m1 is the mass of the Earth = 5.98 x 1024 kg
m2 is the mass of the man = 70 kg
d = 6.38 x 106 m
The value of G = 6.673 x 10-11 N m2/kg2
Now substituting the values in the Gravitational force formula, we get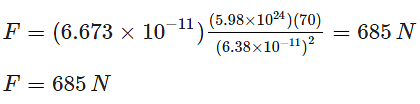
Example 2: A sphere of mass 100 kg is attracted by another spherical mass of 11.75 kg by a force of 19.6 x 10-7 N when the distance between their centers is 0.2 m. Find G.
Solution: Mass of first body = m1 = 100 kg, mass of second body = m2 = 11.75 kg, distance between masses = r = 0.2 m, force between them = F = 19.6 x 10-7 N,
To Find: Universal gravitation constant = G =?
By Newton’s law of gravitation
The value of the universal gravitation constant is 6.672 x 10-11 N m2/kg2.
Example 3: Calculate the gravitational force of attraction between two metal spheres each of mass 90 kg, if the distance between their centers is 40 cm. Given G = 6.67 x 10-11 N m2/kg2. Will the force of attraction be different if the same bodies are taken on the moon, their separation remaining the same?
Solution: Mass of first body = m1 = 90 kg, mass of second body = m2 = 90 kg, Distance between masses = r = 40 cm = 40 x 10-2 m, G = 6.67 x 10-11 N m2/kg2 .
To Find: Force of attraction = F =?
By Newton’s law of gravitation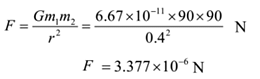
If the same bodies are taken on the moon, their separation remains the same, the force of attraction between the two bodies will remain the same because the force of attraction between two bodies is unaffected by the presence of the third body and medium between the two bodies.
The force of attraction between two metal spheres is 3.377 x 10-6 N.
Example 4: Three 5 kg masses are kept at the vertices of an equilateral triangle each of side of 0.25 m. Find the resultant gravitational force on any one mass. G = 6.67 x 10-11 S.I. units.
Solution: m1 = 5 kg, m2 = 5 kg, m3 = 5 kg, r = 0.25 m, G = 6.67 x 10-11 N m2/kg2.
To find: Force on m1 =?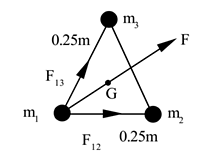 By Newton’s law of gravitation, the force on mass m1 due to mass m2.
By Newton’s law of gravitation, the force on mass m1 due to mass m2.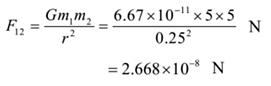
By Newton’s law of gravitation, the force on mass m1 due to mass m3.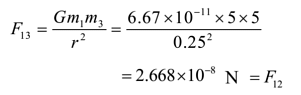 The angle between F12 and F13 is 60°. (Angle of an equilateral triangle). The net force on m1 is given by
The angle between F12 and F13 is 60°. (Angle of an equilateral triangle). The net force on m1 is given by The two forces are equal, hence their resultant act along angle bisector towards centroid.
The two forces are equal, hence their resultant act along angle bisector towards centroid.
Force on any mass is 4.621 x 10-8 N towards the centroid
Example 5: Two bodies of masses 5 kg and 6 x 1024 kg are placed with their centres 6.4 x 106 m apart. Calculate the gravitational force of attraction between the two masses. Also, find the initial acceleration of two masses assuming no other forces act on them.
Solution: Mass of first body = m1 = 5 kg, mass of second body = m2 = 6 x 1024 kg, Distance between masses = r = 6.4 x 106 m, G = 6.67 x 10-11 N m2/kg2 .
To Find: Force of attraction between two masses = F =? Initial accelerations of the two masses =?
Ans:
By Newton’s law of gravitation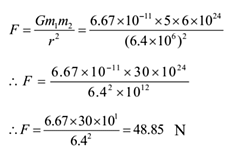
Initial acceleration of the body of mass 5 kg
By Newton’s second law of motion F = ma
Thus a = F/m = 48.85 / 5 = 9.77 m/s2
Initial acceleration of the body of mass 6 x 1024 kg
By Newton’s second law of motion F = ma
Thus a = F/m = 48.85 / 6 x 1024 = 8.142 x 10-24 m/s2
The force of attraction between the two masses = 48.85 N
Mass and Weight
In Newton’s law of gravity, we noticed that the mass is a crucial quantity. We consider mass and weight to be the same, but they are related but are different in reality.
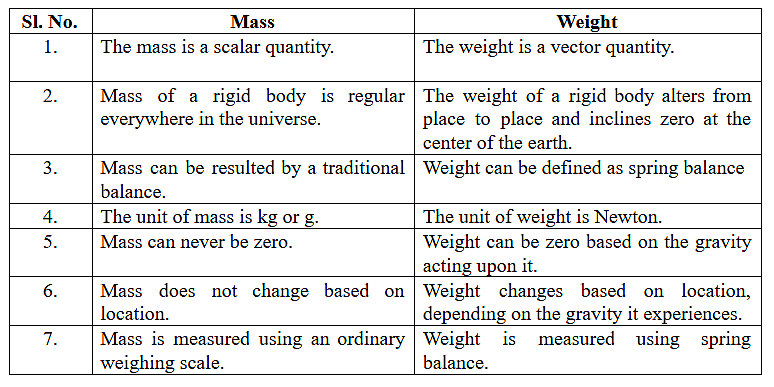
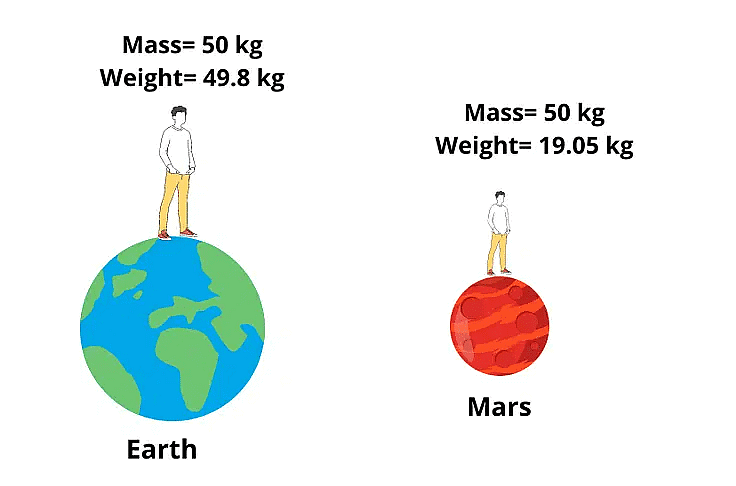 Difference between Mass and Weight
Difference between Mass and Weight
[Question: 906078]
Gravitational Field
We can state by Newton's universal law of gravitation that every mass M produces, in the region around it, a physical situation in which, whenever any other mass is placed, force acts on it, is called gravitational field. This field is recognized by the force that the mass M exerts another mass, such as m, brought into the region.
 Fig: Gravitational field around the earth
Fig: Gravitational field around the earth
Strength of Gravitational Field
We define gravitational field strength at any point in space to be the gravitational force per unit mass on a test mass (mass brought into the field for experimental observation).
Thus for a point in space if a test mass m0, experiences a force  , then at that point in space, gravitational field strength which is denoted by
, then at that point in space, gravitational field strength which is denoted by  , is given as
, is given as 
Gravitational field strength  is a vector quantity and has same direction as that of the force on the test mass in field.
is a vector quantity and has same direction as that of the force on the test mass in field.
Generally magnitude of test mass is very small such that its gravitational field does not modify the field that is being measured.
It should be also noted that gravitational field strength is just the acceleration that a unit mass would experience at that point in space.
Gravitational Field Strength of Point Mass:
As per our previous discussion we can state that every point mass also produces a gravitational field in its surrounding. To find the gravitational field strength due to a point mass, we put a test mass m0 at a point P at distance x from a point mass m then force on m0 is given as:

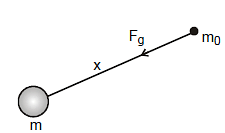
Now if at point P, gravitational field strength due to m is gp then it is given as

The expression written in above equation gives the gravitational field strength at a point due to a point mass.
It should be noted that the expression in equation written above is only applicable for gravitational field strength due to point masses. It should not be used for extended bodies.
However, the expression for the gravitational field strength produced by extended masses has already been derived in electrostatics section.
[Just replace k by -G & Q by M in those expressions].
So we will just revise the expression of gravitational field strength at points due to various extended masses. Gravitational field strength :
1. At a point on the axis of Ring = 
2. At a point on the axis of disc = 
3. At an axial point of a rod = 
4. Due to a circular Arc = 
5. Due to a long infinite thread = 
6. Due to long solid cylinder
(a) at an outer point =  (where r is mass density per volume)
(where r is mass density per volume)
(b) at an inner point = - 2G r πx
7. Due to hollow sphere :
(a) for outer points =  (Behaving as a point mass)
(Behaving as a point mass)
(b) for points on surface =  (Behaving as a point mass)
(Behaving as a point mass)
(c) for inner points = 0 (As no mass is enclosed within it)
8. Due to solid sphere
(a) For outer points =  (Behaving as a point mass)
(Behaving as a point mass)
(b) For points on surface =  (Behaving as a point mass)
(Behaving as a point mass)
(c) For inner points = 
Interaction Energy:
This energy exists in a system of particles due to the interaction forces between the particles of system. Analytically this term is defined as the work done against the interaction of system forces in assembling the given configuration of particles.
To understand this we take a simple example of interaction energy of two points masses.
Figure (a) shows a system of two point masses m1 and m2 placed at a distance r apart in space. here if we wish to find the interaction potential energy of the two masses, this must be the work done in bringing the two masses from infinity (zero interaction state) to this configuration.
For this we first fix m1 at its position and bring m2 slowly from infinity to its location. If in the process m2 is at a distance x from m1 then force on it is



This force is applied by the gravitational field of m1 to m2. If it is further displaced by a distance dx towards m1 then work done by the field is
 =
= 
Now in bringing m2 from infinity to a position at a distance r from m1, the total work done by the field is
 = - G m1 m2
= - G m1 m2

Thus during the process field of system has done  amount of work. The work is positive because the displacement of body is in the direction of force.
amount of work. The work is positive because the displacement of body is in the direction of force.
Initially when the separation between m1 and m2 was very large (at infinity) there was no interaction between them. We conversely say that as a reference when there is no interaction the interaction energy of the system is zero and during the process system forces (gravitational forces) are doing work so system energy will decrease and becomes negative (as initial energy was zero).
As a consequence we can state that in general if system forces are attractive, in assembling a system of particles work will be done by the system and it will spend energy in assembling itself. Thus finally the interaction energy of system will be negative. On the other hand if in a given system of particles, the system forces are repulsive, then in assembling a system some external forces have to be work against the system forces and in this case some work must be done by external forces on the system hence finally the interaction energy of the system of particles must be positive.
In above example as work is done by the gravitational forces of the system of two masses, the interaction energy of system must be negative and it can be given as
 ...(1)
...(1)
As gravitational forces are always attractive, the gravitational potential energy is always taken negative.
Interaction Energy of a System of Particles:
If in a system there are more than two particles then we can find the interaction energy of particle in pairs using equation (1) and finally sum up all the results to get the total energy of the system. For example in a system of N particles with masses m1, m2........mn separated from each other by a distance r12........ where r12 is the separation between m1 and m2 and so on.
In the above case the total interaction energy of system is given as:

In this expression the factor  is taken because the interaction energy for each possible pair of system is taken twice during summation as for mass m1 and m3
is taken because the interaction energy for each possible pair of system is taken twice during summation as for mass m1 and m3
 =
= 
Now to understand the applications of interaction energy we take few examples.
Ex. 1 Three particles each of the mass m are placed at the corners of an equilateral triangle of side d and shown in figure. Calculate (a) the potential energy of the system, (b) work done on this system if the side of the triangle is changed from d to 2d.
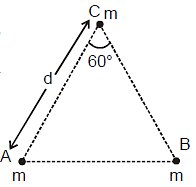
Sol. (a) As in case of two-particle system potential energy is given by (-Gm1m2/r), so
U = U12 + U23 + U31 or 
(b) When d is changed to 2d,
Uf = - 
Thus work done in changing in potential energy is given as
W = Uf - Ui = 
Ex. 2 Two particles m1 and m2 are initially at rest at infinite distance. Find their relative velocity of approach due to gravitational atraction when their separation is d.
Sol. Initiallly when the separation was large there was no interaction energy and when they get closer the system gravitational energy decreases and the kinetic energy increases.
When separation between the two particles is d, then according to energy conservation we have

As no other force is present we have according to momentum conservation
m1v1 = m2v2
From equations written above
 or
or 
And on further solving we get

Thus approach velocity is given as

Ex. 3 If a particle of mass 'm' is projected from a surface of bigger sphere of mass '16M' and radius '2a' then find out the minimum velocity of the particle such that the particle reaches the surface of the smaller sphere of mass M and radius 'a'. Given that the distance between the centres of two spheres is 10 a.
Sol. When the particle is at the surface of bigger sphere it is attracted more by the bigger sphere and less by the smaller sphere. As it is projected the force of attraction from bigger sphere decreases and that from smaller sphere increass and thus the particle reaches the state of equilibrium at distance x from the centre smaller sphere
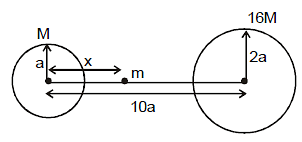

(10a - x)2 = 16x2
10a - x = 4x ⇒ x = 2a
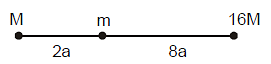
After this point the attraction on the particle from the smaller sphere becomes more than that from the bigger sphere and the particle will automatically move towards the smaller sphere. Hence the minimum velocity to reach the smaller sphere is the veloicty required to reach the equilibrium state according to energy conservation, we have,

 ⇒
⇒ 
Gravitational Potential
The gravitational potential at a point in gravitational field is the gravitational potential energy per unit mass placed at that point in gravitational field. Thus at a certain point in gravitational field, a mass m0 has a potential energy U then the gravitational potential at that point is given as:
V = 
or if at a point in gravitational field gravitational potential V is known then the interaction potential energy of a point mass m0 at that point in the field is given as
U = m0v
Interaction energy of a point mass m0 in a field is defined as work done in bringing that mass from infinity to that point. In the same fashion we can define gravitational potential at a point in field, alternatively as "Work done in bringing a unit mass from infinity to that point against gravitational forces."
When a unit mass is brought to a point in a gravitational field, force on the unit mass is  at a point in the field. Thus the work done in bringing this unit mass from infinity to a point P in gravitational field or gravitational potential at point P is given as
at a point in the field. Thus the work done in bringing this unit mass from infinity to a point P in gravitational field or gravitational potential at point P is given as

Here negative sign shown that VP is the negative of work done by gravitation field or it is the external required work for the purpose against gravitational forces.
Gravitational Potential due to a Point Mass:
We know that in the surrounding of a point mass it produces its gravitational field. If we wish to find the gravitational potential at a point P situated at a distance r from it as shown in figure,
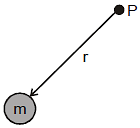
we place a test mass m0 at P and we find the interaction energy of m0 with the field of m, which is given as

Now the gravitational potential at P due to m can be written as

The expression of gravitational potential in equation is a standard result due to a point mass which can be used as an elemental form to find other complex results, we'll see later.
The same thing can also be obtained by using equation
 or
or  or
or 
Gravitational potential:
1. Due to a rod at an a xial point = - Glln 
2. Due to ring at an axial point = 
3. Due to ring at the centre = 
4. Due to Disc =  (where s is mass density per unit area)
(where s is mass density per unit area)
5. Due to hollow sphere
for outer points = 
For surface points = 
For inner points = 
6. Due to solid sphere

For outer points = 
For surface points = 
For inner points = 
Potential energy of hollow sphere = 
Potential energy of solid sphere = 
Gravitational Lines of Forces:
Gravitational field can also be represented by lines of force. A line of force is drawn in such a way that at each point the direction of field is tangent to line that passes through the point. Thus tangent to any point on a line of force gives the direction of gravitational field at that point. By convention lines of force are drawn in such a way that their density is proportional to the strength of field.
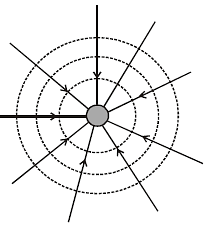
Figure shown shows the field of a point mass in its surrounding. We can see that the lines of force are radially inward giving direction of field and as we go closer to the mass the density of lines is more which shows that field strength is increasing.
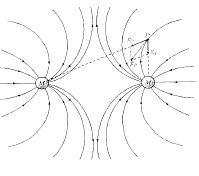
Figure shown shows the configuration of field lines for a system of two equal masses separated by a given distance.
Here we can see that there is no point where any two lines of force intersects or meet. The reason is obvious that at one point in space there can never be two direction of gravitational fields. It should be noted that a line of force gives the direction of net gravitational field in the region. Like electric field gravitational field never exists in closed loops.
- Gravitational Flux :

- Gravitational Gauss law :

Here  is the gravitational field due to all the masses. Min is the mass inside the assumed gaussian surface.
is the gravitational field due to all the masses. Min is the mass inside the assumed gaussian surface.
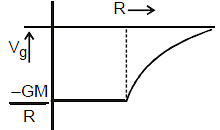
Acceleration due to Gravity
We can consider earth to be a very large sphere of mass Me and radius Re. Gravitational field strength due to earth is also regarded as acceleration due to gravity or gravitational acceleration. Now we find values of g at different points due to earth.
- Earth behaves as a non conducting solid sphere.
Value of g on Earth's Surface:

If gs be the gravitational field strength at a point A on the surface of earth, then it can be easily obtained by using the result of a solid sphere. Thus for earth, value of gs can be given as
 ...(1)
...(1)
Value of g at a Height h Above the Earth's Surface:

If we wish to find the value of g at a point P as shown in figure shown at a height h above the Eath's surface. Then the value can be obtained as
 or
or 
If point P is very close to Earth's surface then for h << Re we can rewrite the expression in given equation as

 [Using binomial approximation] ...(2)
[Using binomial approximation] ...(2)
Value of g at a Depth h Below the Earth's Surface:
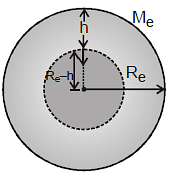
If we find the value of g inside the volume of earth at a depth h below the earth's surface at point P as shown in figure, then we can use the result of g inside a solid sphere as

Here x, the distance of point from centre of earth is given as
x = Re - h
Thus we have  ...(3)
...(3)
From equation (1), (2) and (3) we can say that the value of g at earth's surface is maximum and as we move above the earth's surface or we go below the surface of earth, the value of g decrease.
Effect of Earth's Rotation on Value of g
Let us consider a body of mass m placed on Earth's surface at a latitude q as shown in figure. This mass experiences a force mgs towards the centre of earth and a centrifugal force mwe2 Re sinθ relative to Earth's surface as shown in figure.
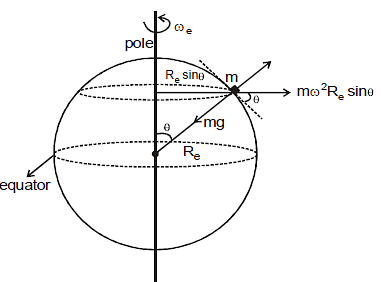
If we consider geff as the effective value of g on earth surface at a latitude q then we can write
geff =  =
= 
 is very very small
is very very small
So we can write 
 » g - we2 R sin2q ...(i)
» g - we2 R sin2q ...(i)
From equation (1) we can find the value of effective gravity at poles and equatorial points on Earth as
At poles q = 0 ⇒ gpoles = gs = 9.83 m/s2
At equator q =  ⇒ gequator = gs - w2Re = 9.78 m/s2
⇒ gequator = gs - w2Re = 9.78 m/s2
Thus we can see that the body if placed at poles of Earth, it will only have a spin, not circular motion so there is no reduction in value of g at poles due to rotation of earth. Thus at poles value of g on Earth surface is maximum and at equator it is minimum. But an average we take 9.8 m/s2, the value of g everywhere on earth's surface.
Effect of Shape of Earth on Value of g
Till now we considered that earth is spherical in its shape but this is not actually true. Due to some geological and astronomical reasons, the shape of earth is not exact spherical. It is ellipsoidal.
As we've discussed that the value of g at a point on earth surface depends on radius of Earth.It is observed that the approximate difference in earth's radius at different points on equator and poles is re - rp 21 to 34 km.
Due to this the difference in value of g at poles and equatorial points is approximately gp - ge 0.02 to 0.04 m/s2, which is very small.
So for numerical calculations, generally, we ignore this factor while taking the value of g and we assume Earth is spherical in shape.
Ex. 4 Calculate the mass and density of the earth. Given that Gravitational constant G = 6.67 × 10-11 Nm2/kg2, the radius of the earth = 6.37 × 106 m and g = 9.8 m/s2.
Sol. The acceleration due to gravity on earth surface is given as
ge =  or
or  = 6 × 1024 kg
= 6 × 1024 kg
If r be the density of earth, then
M =  or r =
or r =  =
=  = 5.5 × 103 kg/m3
= 5.5 × 103 kg/m3
Ex. 5 If the radius of the earth were to shrink by one percent, its mass remaining the same, what would happen to the acceleration due to gravity on the earth's surface?
Sol. Consider the case of body of mass m placed on the earth's surface (mass of the earth M and radius R). If g is acceleration due to gravity, then we known that
gs =  ...(1)
...(1)
Now, when the radius is reduced by 1%, i.e. radius becomes 0.99 R, let acceleration due to gravity be g', then
 ...(2)
...(2)
From equation (1) and (2), we get
 or
or  or g' = 1.02 g
or g' = 1.02 g
Thus, the value of g is increased by 2%.
Ex. 6 At what rate should the earth rotate so that the apparent g at the equator becomes zero? What will be the length of the day in this situation ?
Sol. At earth's equator effective value of gravity is
geq = gs - w2Re
If geff at equator is zero, we have
gs = w2Re or 
Thus length of the day will be  = 2 × 3.14
= 2 × 3.14 
Ex. 7 Calculate the acceleration due to gravity at the surface of Mars if its diameter is 6760 km and mass is one-tenth that of earth. The diameter of earth is 12742 km and acceleration due to gravity on earth is 9.8 m/s2.
We know that 
So  ⇒
⇒  or gM = 9.8 × 0.35 = 3.48 m/s2
or gM = 9.8 × 0.35 = 3.48 m/s2
Ex. 8 Calculate the apparent weight of a body of mass m at a latitude l when it is moving with speed v on the surface of the earth from west to east at the same latitude.
Sol.
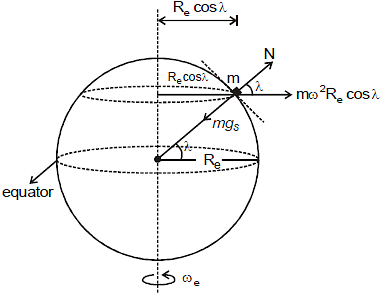
If W be the apparent weight of body at a latitude l then from figure shown, we have
W = mg - mw2R cos2λ ...(1)
When body moves at speed v from west to east relative to earth, its net angular speed w can be given as
 [we ® earth's angular velocity]
[we ® earth's angular velocity]
Now from equation (1) we have

or 

 [Neglecting
[Neglecting  as being very small]
as being very small]
|
97 videos|378 docs|103 tests
|
FAQs on Gravitation & Related Terms - Physics Class 11 - NEET
| 1. What is Newton's Law of Universal Gravitation? |  |
| 2. What are the properties of gravitational force? |  |
| 3. What is the gravitational equation in vector form? |  |
| 4. What is the difference between mass and weight? |  |
| 5. What are some related terms in gravitation? |  |

|
Explore Courses for NEET exam
|

|


















