Energy of a Satellite | General Awareness - Bank Exams PDF Download
Energies of a Satellite in a Circular Orbit
When there is a satellite revolving in a stable circular orbit of radius r around the earth, its speed is given by the above equation. During its motion, the kinetic energy of the satellite can be given as
As the gravitational force on the satellite due to the earth is the only force it experiences during motion, it has gravitational interaction energy in the field of the earth, which is given as
Thus the total energy of a satellite in an orbit of radius r can be given as
Total energy E = Kinetic energy + K Potential Energy U
or
We can see that,
The above relation in the magnitude of total, kinetic and potential energies of a satellite is very useful in numerical problems so it is advised to keep this relation in mind while handling satellite problems related to energy.
Now to understand satellite and planetary motion in detail, we take a few examples.
Example 1: Estimate the mass of the sun, assuming the orbit of the earth round the sun to be a circle. The distance between the sun and earth is 1.49 × 1011 m and G = 6.66 × 10-11 Nm2/kg2.
Solution:
Here the revolving speed of the earth can be given as
[Orbital speed]
Where M is the mass of the sun and r is the orbit radius of the earth.
We know time period of Earth around the sun is T = 365 days, thus we have
T =
or or
M = =
= 1.972 × 1022 kg
Example 2: If the earth is one-half of its present distance from the sun, how many days will be in one year ?
Solution: If the orbit of earth's radius is R, in the previous example we've discussed that time period is given as,
If the radius changes or r' = , new time period becomes
From the above equations, we have
or
=
Example 3: A satellite revolving in a circular equatorial orbit of radius r = 2.00 × 104 km from west to east appears over a certain point at the equator every t = 11.6 hours. Using this data, calculate the mass of the earth. The gravitational constant is supposed to be known.
Solution: Here the absolute angular velocity of the satellite is given by
ω = ωs + ωE
Where wE is the angular velocity of the earth, which is from west to east.
or [Where t = 11.6 hr. and T = 24 hr.]
From Kepler's III law, we have
Thus we have
or = 6.0 × 1024 kg
Example 4: A satellite of mass m is moving in a circular orbit of radius r. Calculate its angular momentum with respect to the centre of the orbit in terms of the mass of the earth.
Solution: The situation is shown in the figure
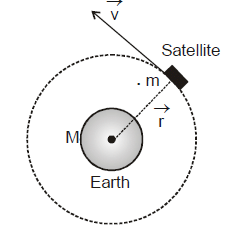
The angular momentum of the satellite with respect to the centre of orbit is given by
where is the position vector of the satellite with respect to the centre of orbit and
is its velocity vector of the satellite.
In the case of a circular orbit, the angle between and
is 90°. Hence
L = m v r sin 90° = m v r
The direction is perpendicular to the plane of the orbit.
We know the orbital speed of the satellite is
⇒
Now we will understand the concept of the double star system through an example.
Example 5: In a double star, two stars of masses m1 and m2. distance d apart revolves around their common centre of mass under the influence of their mutual gravitational attraction. Find an expression for the period T in terms of masses m1, m2 and d. Find the ratio of their angular momenta about the centre of mass and also the ratio of their kinetic energies.
Sol. The centre of mass of the double star from mass m1 is given by
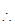 The distance of the centre of mass from m2 is
The distance of the centre of mass from m2 is
Both the stars rotate around the centre of mass in their circular orbits with the same angular speed ω.
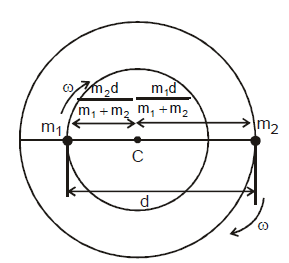
the gravitational force acting on each star provides the necessary centripetal force. if we consider the rotation of mass m1, then
or
This gives w = =
or Period of revolution
The ratio of Angular Momenta is
The ratio of kinetic energies is
Motion of a Satellite in Elliptical Path
Whenever a satellite is in a circular or elliptical path, these orbits are called bounded orbits as the satellite is moving in an orbit bounded to Earth. The bound nature of orbit means that the kinetic energy of the satellite is not enough at any point in the orbit to take the satellite to infinity. In equation shows the negative total energy of a revolving satellite shows its boundness to Earth. Even when a body is in an elliptical path around the earth, its total energy must be negative. Let's first discuss how a satellite or a body can be in an elliptical path.
Consider a body (satellite) of mass m in a circular path of radius r around the earth as shown in the figure. we've discussed that in a circular path, the net gravitational frame on the body is exactly balancing the centrifugal force on it in a radial direction relative to a rotating frame with the body.
If suddenly the velocity of the body decreases then the centrifugal force on it becomes less than the gravitational force acting on it and due to this it can not continue in the circular orbit and will come inward from the circular orbit due to unbalanced force. Mathematical analysis shows that this path-I along which the body is now moving is an ellipse. The analytical calculations of the laws for this path are beyond the scope of this book. But it should be kept in mind that if the velocity of a body at a distance r from the earth's centre tangential to the circular orbit is less than then its path will be elliptical with earth's centre at one of the foci of the ellipse.
Similarly, if the speed of the body exceeds then it must move out of the circular path due to unbalancing of forces again but this time Fe > Fg. Due to this if the speed of the body is not increased by such a value that its kinetic energy can take the particle to infinity then it will follow in a bigger elliptical orbit as shown in figure in path-II, with earth's at one of the foci of the orbit.
In the above case when the speed of the body was decreased and its value is lesser than and the speed is decreased to such a value that the elliptical orbit will intersect the earth's surface as shown in the figure, then the body will follow an arc of the ellipse and will fall back to earth.
Satellite Motion and Angular Momentum Conservation
We've discussed that when a body is in bounded orbit around a planet it can be in a circular or elliptical path depending on its kinetic energy at the time of launching. Let's consider a case when a satellite is launched in an orbit around the earth.
A satellite S is first fired away from the earth's source in the vertical direction to penetrate the earth's atmosphere. When it reaches point A, it is imparted a velocity in the tangential direction to start its revolution around the earth in its orbit.
This velocity is termed insertion velocity, if the velocity imparted to the satellite is then it starts following the circular path shown in the figure. If the velocity imparted is v1 > v0 then it will trace the elliptical path shown. During this motion, the only force acting on the satellite is the gravitational force due to Earth which is acting along the line joining the satellite and the centre of earth.
As the force on the satellite always passes through the centre of the earth during motion, we can say that on a satellite there is no torque acting about the centre of the earth thus total angular momentum of the satellite during orbital motion remains constant about the earth's centre.
As no external force is involved for the earth-satellite system, no external work is being done here so we can also state that the total mechanical energy of the system also remains conserved.
In the elliptical path of the satellite shown in the figure if r1 and r2 are the shortest distance (perigee) and farthest distance (apogee) of the satellite from Earth and at the points, velocities of the satellite are v1 and v2 then we have according to the conservation of angular momentum, the angular momentum of the satellite at a general point is given as
L = mv1r1 = mv2r2 = mvr sinθ
During motion, the total mechanical energy of a satellite (kinetic potential) also remains conserved. Thus the total energy of the satellite can be given as
Using the above relations in the equation written above we can find velocities v1 and v2 of satellites at nearest and farthest locations in terms of r1 and r2.
|
365 videos|701 docs|149 tests
|
FAQs on Energy of a Satellite - General Awareness - Bank Exams
| 1. What is the energy of a satellite? |  |
| 2. How is the energy of a satellite calculated? |  |
| 3. How does the energy of a satellite affect its orbit? |  |
| 4. Can the energy of a satellite be changed? |  |
| 5. How does the energy of a satellite relate to its stability? |  |






















