Doppler's Effect : Definition, Formula and Applications | Physics Class 11 - NEET PDF Download
You must have heard or read that our universe is expanding. Edwin Hubble noticed that the light from distant galaxies was shifted toward lower frequencies to the red end of the spectrum. When stars or galaxies are moving away from us, we see their color as red-shifted. This is called Doppler's effect. In this document, we will study this effect in detail.
What is Doppler's Effect?
The Doppler effect in physics refers to the alteration of the frequency of waves, such as sound, light, or others, as the source and observer move closer to or farther away from each other.
This phenomenon was first proposed by Christian Johann Doppler in 1842.
 Doppler Effect
Doppler Effect
Doppler Effect Formula
The Doppler effect refers to the perceived alteration in wave frequency resulting from the relative movement between the sound source and the observer. We can determine the apparent frequency in the Doppler effect by employing the following equation:
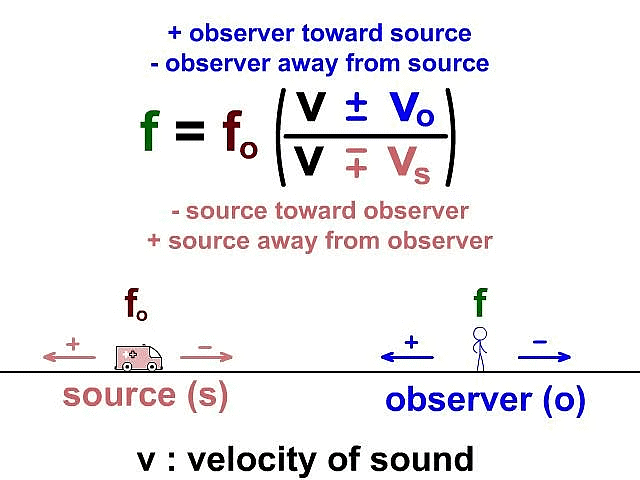 Doppler effect formula
Doppler effect formula
The above equation changes in different situations depending on the velocities of the observer or the source of the sound.
Case 1: Stationary Source and Stationary Observer
The figure shows a stationary source of frequency n0 which produces sound waves in the air of wavelength l0 given as:
- Although sound waves are longitudinal, here we represent sound weaves by the transverse displacement curve as shown in the figure to understand the concept in a better way.
- As the source produces waves, these waves travel towards, stationary observer O in the medium (air) with speed v and wavelength l0.
- As the observer is at rest here it will observe the same wavelength l0 is approaching it with speed v so it will listen to the frequency n given as:
This is why when a stationary observer list ends the sound from a stationary source of sound, it detects the same frequency sound that the source is producing. Thus no Doppler effect takes place if there is no relative motion between the source and the observer.
Case 2: Stationary Source and Moving Observer
The figure shows the case when a stationary source of frequency n0 produces sound waves that have a wavelength in the air given as:
- These waves travel toward the moving observer with velocity v0 towards, the source. When sound waves approach the observer, they will receive the waves of wavelength l0 with speed v0 (relative speed).
Thus the frequency of sound heard by the observer can be given as
Apparent frequency nap = Similarly, we can say that if the observer is receding away from the source the apparent frequency heard by the observer will be given as
Case 3: Moving Source and Stationary Observer
The figure shows the situation when a moving source S of frequency n0 produces sound waves in medium (air) and the waves travel toward the observer with velocity v.
- Here if we carefully look at the initial situation when the source starts moving with velocity vs as well as it starts producing waves.
- The period of one oscillation is
sec and in this duration source emits one wavelength l0 in the direction of propagation of waves with speed v, but in this duration, the source will also move forward by a distance vs
.
- Thus the effective wavelength of emitted sound in air is slightly compressed by this distance as shown in the figure. This is termed as the apparent wavelength of sound in a medium (air) by the moving source. This is given as:
Apparent wavelength
Now this wavelength will approach the observer with speed v ( O is at rest). Thus the frequency of sound heard by the observer can be given as, Apparent frequency :
Similarly, if the source is receding away from the observer, the apparent wavelength emitted by the source in the air toward the observer will be slightly expanded and the apparent frequency heard by the stationary observer can be given as
Case 4: Moving Source and Moving Observer
Let us consider the situation when both source and observer are moving in the same direction as shown in the figure at speeds vs and v0 respectively.
- In this case, the apparent wavelength emitted by the source behind it is given as
- Now this wavelength will approach the observer at relative speed v v0 thus the apparent frequency of sound heard by the observer is given as
- By looking at the expression of apparent frequency given by the equation, we can easily develop a general relation for finding the apparent frequency heard by a moving observer due to a moving source as
- Here + and - signs are chosen according to the direction of motion of the source and observer. For both source and observer v0 and vs are taken in equation with a -ve sign if they are moving in the direction of
i.e. the direction of propagation of sound from a source to the observer. For both source and observer v0 and vs are taken with a -ve sign if they are moving in the direction opposite to
i.e. opposite to the direction of propagation of sound from the source to the observer.
Doppler Effect in Reflected Sound
- When a car is moving toward a stationary wall as shown in the figure, if the car sounds a horn, a wave travels towards the wall and is reflected from the wall.
- When the reflected wave is heard by the driver, it appears to be of relatively high pitch. If we wish to measure the frequency of reflected sound then the problem must be handled in two steps.
Reflected sound
- First, we treat the stationary wall as a stationary observer and the car as a moving source of sound of frequency n0. In this case, the frequency received by the wall is given as:
- Now wall reflects this frequency and behaves like a stationary source of sound of frequency n1 and the car (driver) behaves like a moving observer with velocity vc. Here the apparent frequency heard by the car driver can be given as:
- The same problem can also be solved in a different manner by using the method of sound images. In this procedure, we assume the image of the sound source behind the reflector. In the previous example we can explain this by the situation shown in the figure:
Doppler effect in reflected sound
- Here we assume that the sound which is reflected by the stationary wall is coming from the image of the car which is at the back of it and coming toward it with velocity vc. Now the frequency of sound heard by car driver can directly be given as:
nap = n0
- This method of images for solving problems of the Doppler effect is very convenient but is used only for velocities of source and observer which are very small compared to the speed of sound and it should not be used frequently when the reflector of sound is moving.
Doppler's Effect for Accelerated Motion
- For the case of a moving source and a moving observer, we know the apparent frequency observer can be given as
- Here v is the velocity of sound and v0 and vs are the velocity of observer and source respectively. When a source of the observer has accelerated or retarded motion then we use that value of v0 at which the observer receives the sound and for the source, we use that value of vs at which it has emitted the wave.
- The alternative method of solving this case is the traditional method of compressing or expending the wavelength of sound by the motion of the source and using the relative velocity of sound with respect to the observer.
Doppler's Effect when the line of motion is different
- Consider the situation shown in the figure. Two cars 1 and 2 are moving along perpendicular roads at speeds v1 and v2. When car 1 sounds a horn of frequency n0, it emits sound in all directions and says car 2 is at the position, shown in the figure, when it receives the sound.
- In such cases we use velocity components of the cars along the line joining the source and observer thus the apparent frequency of sound heard by car 2 can be given as
Doppler's effect when the line of motion is different.
Applications of Doppler's Effect
A common misconception is that the Doppler effect is exclusively relevant to sound waves, but in reality, it applies to all kinds of waves, including light. Here, we've outlined a number of applications for the Doppler effect :
- Sirens
- Radar
- Astronomy
- Medical Imaging
- Blood Flow Measurement
- Satellite Communication
- Vibration Measurement
- Developmental Biology
- Audio
- Velocity Profile Measurement
Summary
The following table summarizes the important formulas of various cases of Doppler's effect:
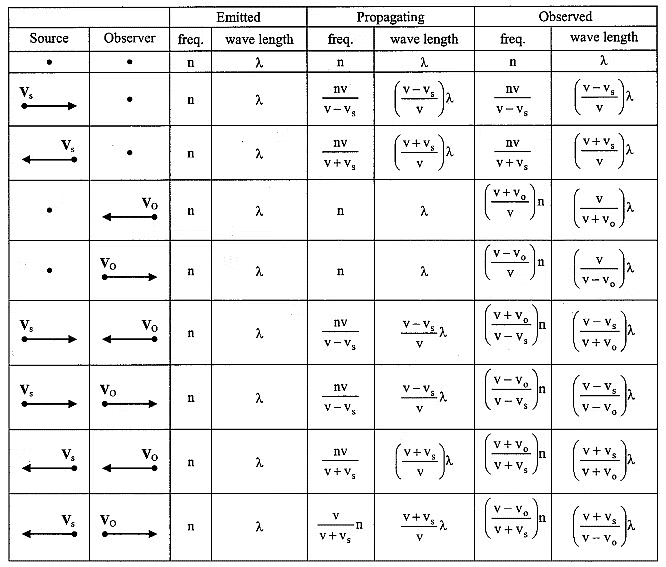
|
95 videos|367 docs|98 tests
|
FAQs on Doppler's Effect : Definition, Formula and Applications - Physics Class 11 - NEET
| 1. What is the Doppler Effect? |  |
| 2. What is the formula for the Doppler Effect? |  |
| 3. How does the Doppler Effect work in reflected sound? |  |
| 4. How does the Doppler Effect apply to accelerated motion? |  |
| 5. What happens if the line of motion is different between the observer and the source? |  |

















