Relation - Commerce PDF Download
Relations and Functions
Relation
If A and B are two non-empty sets, then a relation R from A to B is a subset of A x B.
If R ⊆ A x B and (a, b) ∈ R, then we say that a is related to b by the relation R, written as aRb.
Cartesian product
The Cartesian product ( also known as the cross product) of two sets A and B, denoted by AxB (in the same order) is the set of all ordered pairs ( x, y) such that x∈A and y∈B. What we mean by ordered pair is that the pair (a, b) is not the same the pair as (b, a) unless a = b. It implies that AxB ≠ BxA in general. Also if A contains m elements and B contains n elements then AxB contains mxn elements.
Similarly we can define AxA = {(x, y); x∈A and y∈A}. We can also define cartesian product of more than two sets.
e.g. A1x A2xA3 x . . . .x An = {( a1, a2, . . . , an): a1 ∈A1, a2 ∈ A2, . . . , an ∈ An}
Illustration:-
If A = {a, b, c} and B = {b, c, d} then evaluate
i). A∪B, A∩B, A–B and B–A
ii). AxB and BxA
Solution:
i) A∪B = {x: x∈A or x∈B}= {a, b, c, d}
A∩B = {x: x∈A and x∈B}= {b, c}
A-B = {x: x∈A and x ∉ B}= {a}
B-A = {x: x∈B and x∉B}= {d}
ii) AxB = {( x, y): x∈A and y∈B}
= {( a, b), (a, c), ( a, d), ( b, b), ( b, c), ( b, d), (c, b), ( c, c), ( c, d)}
BxA = {(x, y): x∈B and y∈A}
= {( b, a), ( b, b), ( b, c), ( c, a), ( c, b), ( c, c),( d, a), (d, b), (d, c)}
Note that AxB ≠ BxA.
Let A and B be two non-empty sets then every subset of A x B defines a relation from A to B and every relation from A to B is subset of A x B.
Let R ⊆ A x B and ( a, b) ∈ R. then we say that a is related to b by the relation R and write it as a R b. If ( a, b) ∉ R, we write it as ab.
Example
Let A {1, 2, 3, 4, 5}, B = {1, 3}
We set a relation from A to B as: a R b iff a £ b; a ∈ A, b ∈ B. Then
R = {( 1, 1), ( 1, 3), ( 2, 3), ( 3, 3)} ⊂ AxB
Domain and Range of a Relation:
Let R be a relation from A to B, that is, let R ⊆ A x B. Then
Domain R = {a: a ∈ A, ( a, b) ∈ R for some b ∈ B}
i.e. domain of R is the set of all the first elements of the ordered pairs which belong to R.
Also Range R = {b: b ∈ B, ( a, b) ∈ R for some a ∈ A},
i.e. range R is the set of all second elements of the ordered pairs which belong to R.
Thus Dom. R ⊆ A, Range R ⊆ B.
Total Number of Distinct Relations from A to B:
Suppose the set A has m elements and the set B has n elements. Then the product set A x B i.e. P (A x B) will have 2mn elements. A x B has 2mn different subsets which are different relations from A to B.
Inverse Relation:
Let R ⊆ A x B be a relation from A to B. Then inverse relation R–1 ⊆ B x A is defined by
R–1 = {( b, a): ( a, b) ∈ R, a ∈ A, b ∈ B}. It is clear that a R b ↔ b R–1 a
dom R–1 = range R and range R–1 = dom R( R–1)–1 = R
Example: Let A = {1, 2, 3, 4}, B = {a, b, c} and R = { (1, a), (1, c), (2, a)}. Then
i) dom R = {1, 2}, range R = {a, c}
ii) R–1 = { (a, 1), (c, 1), (a, 2)}
Compositions of Relations:
Let R ⊆ A x B, S ⊆ B x C be two relations. Then compositions of the relations R and S denoted by So R ⊆ AxC and is defined by ( a, c) ∈ ( S o R) iff b ∈ B such that ( a, b) ∈ R, ( b, c) ∈ S.
Example:
Let A = {1, 2, 3}, B = {a, b, c, d}, C = {a, b, g}
R ⊆ (A x B) = { (1, a), (1, c), (2, d)}
S ⊆ (B x C) = { (a, a), (a, g), (c, b)}
Then S o R ⊆ (A x C) = {( 1, a), ( 1, g), ( 1, b)}
One should be careful in computing the relation R o S. Actually S o R starts with R and R o S starts with S. In general S o R ≠ R o S
Also ( S o R)–1 = R–1 o S–1, known as reversal rule.
Relations in a Set:
Let R be a relation from A to B. If B = A, then R is said to be a relation in A. Thus relation in a set A is a subset of A x A.
Identity Relation:
R is an identity relation if (a, b) ∈ R iff a = b, a ∈ A, b ∈ A. In other words, every element of A is related to only itself.
Universal Relation in a Set:
Let A be any set and R be the set A x A, then R is called the Universal Relation in A.
Void Relation in a Set:
ϕ is called Void Relation in a set.
Reflexive Relations:
R is a reflexive relation if ( a, a) ∈ R, ” a ∈ A. It should be noted if there is at least one element a ∈ A such that (a, a) ∉ R, then R is not reflexive.
Example:
Let A = {1, 2, 3, 4, 5}
R = { (1, 1), (3, 2), (4, 2), (4, 4), (5, 2), ( 5, 5)} is not reflexive because 3 ∈ A and (3, 3) ∉ R.
R = {(1, 1), (3, 2), (2, 2), (3, 3), (4, 1), (4, 4), (5, 5)} is reflexive since (a, a) ∈ R, ” a ∈ A.
Symmetric Relations:
R is called a symmetric relation on A if (x, y) ∈ R ⇒ (y, x) ∈ R
That is, y R x whenever x R y.
It should be noted that R is symmetric iff R–1 = R
Let A = {1, 2, 3}, then R = {≤ (1, 1), ≤ (1, 3), ≤ (3, 1)} is symmetric.
Anti-symmetric Relations:
R is called a anti-symmetric relation if (a, b) ∈ R and ( b, a) ∈ R ⇒ a = b
Thus, if a ≠ b then a may be related to b or b may be related to a, but never both.
Or, we have never both a R b and b R a except when a = b.
Example:
Let N be the set of natural numbers. A relation R ⊆ N x N is defined by
x R y iff x divides y ≤ i.e. x/y)
Then x R y, y R x ⇒ x divides y, y divides x ⇒ x = y.
Transitive Relations:
R is called a transitive relation if (a, b) ∈ R, (b, c) ∈ R ⇒ (a, c) ∈ R
In other words if a is related to b, b is related to c, then a is related to c.
Transitivity fails only when there exists a, b, c such that a R b, b R c but ac.
Example:
Consider the set A = {1, 2, 3} and the relation
R1 = { (1, 2), (1, 3)}
R2 = { (1, 2)}
R3 = { (1, 1)}
R4 = { (1, 2), (2, 1), (1, 1)}
Then R1, R2 and R3 transitive while R4 is not transitive since in R4, (2, 1) ∈ R4, (1, 2) ∈ R4 but ( 2, 2) ∉ R4
Note:
It is interesting to note that every identity relation is reflexive but every reflexive relation need not be an identity relation. Also identity relation is reflexive, symmetric and transitive.
Equivalence Relation:
A relation R in a set A is called an equivalence relation if
R is reflexive i.e., (a, a) ∈ R, ” a ∈ A
R is symmetric i.e., ≤( a, b) ∈ R ⇒ ≤ (b, a) ∈ R
R is transitive i.e., ≤ (a, b), ≤ b, c) ∈ R ⇒ ≤ (a, c) ∈R
The equivalence relation is usually denoted by the symbol ~.
Equivalence Classes of an Equivalence Relation:
Let R be equivalence relation in A ( ≠ ϕ). Let a ∈ A.
Then the equivalence class of a denoted by [a] or {} is defined as the set of all those points of A which are related to a under the relation R. Thus [a] = {x : x ∈ A, x R a}
It is easy to see that
b ∈ [a] ⇒ a ∈ [b]
b ∈ [a] ⇒ [a] = [b]
Two equivalence classes are either disjoint of identical.
as an example we consider a very important relation x º y (mod n) iff n divides (x –y), is fixed positive integer. Consider n = 5 then
[0] = {x : x º 0 ( mod 5)} = {5p : p ∈ z} = {0, ±5, ±10, ±15,….}
[1] = {x : x º 1 ( mod 5)} = {x : x –1 = 5k, k ∈ z} = {5k + 1: k ∈ z} = {1, 6, 11, …., –4, –9,….}
one can easily see that there are only 5 distinct equivalence classes viz. [0], [1], [2], [3] and [4] when n = 5.
Illustration-:
N is the set of natural numbers. The relation R is defined on N x N as follows:
( a, b) R ( c, d) ↔ a + d = b + c
Prove that R is equivalence relation.
Solution:
i) (a, b) R (a, b) ↔ a + b = b + a
∴R is reflexive.
ii) (a, b) R (c, d) ⇒ a + d = b + c
⇒ c + b = d + a
⇒ (c, d) R (a, b)
∴R is symmetric.
Now iii) a, b) R (c, d) and ( c, d) R e, f) ⇒ a + d = b + c & c + f = d + e
⇒ a + d + c + f = b + c + d + e
⇒ a + f = b + e ⇒ (a, b) R ( e, f)
R is transitive. Thus R is an equivalence relation on N x N.
Illustration-: A relation R on the set of complex numer is defined by z1 R z2 ⇔ 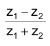 is real, show that R is an equivalence relation.
is real, show that R is an equivalence relation.






∴ R is transitive
Hence R is equivalence relation.
Let m be a positive integer, then the two integer a and b said to be congurent modulo mλ' if a-b is divisible by m i.e a-b = mλ where λ is an positive integer. The congurent modulo m' is defined on all a, b ? | by a≡b = mod m, iff a-b = λ, λ ? I+
Illustration-: Find all congruent solutions of 8x ≡ 6(mod 14)
Solutions:
given
8x ≡ 6(mod 14)

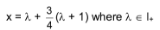
and here greatest common divisor of 8 and 14 is 2 so, there are two required solutions for λ = 3 and λ = 7, x = 6, 13
FAQs on Relation - Commerce
| 1. What is relation commerce? |  |
| 2. How does relation commerce benefit businesses? |  |
| 3. What strategies can businesses employ for effective relation commerce? |  |
| 4. How can relation commerce be integrated with e-commerce platforms? |  |
| 5. How can businesses measure the success of their relation commerce efforts? |  |

|
Explore Courses for Commerce exam
|

|


















