Distance of a Point from a Line and Distance between two Parallel Lines | Mathematics (Maths) Class 11 - Commerce PDF Download
F. Distance Between Point & Line And Two Parallel Lines
(1) Length of the Perpendicular from a Point on a Line :
The length of the perpendicular from P(x1, y1) on ax + by + c = 0 is
The length of the perpendicular from origin on ax + by + c = 0 is
(2) The distance between two parallel lines :
The distance between two parallel lines : ax + by + c1 = 0 and ax + by + c2 = 0 is 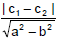
(3) Area of parallelogram with given sides :
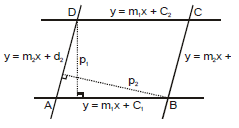
(4) Condition of parallelogram as shown becomes a rhombus :
(5) Reflection (Image) of a point P(a, b) about a line (ax + by + c = 0)
(6) Foot of perpendicular from a point 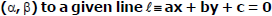
(7) Shifting of the origin :
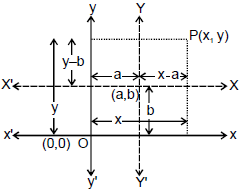
x, y ⇒ old co-ordinates axes
X, Y ⇒ New co-ordinate axes
X = 0 ⇒ x - a = 0 ⇒ x = a
Y = 0 ⇒ y - b = 0 ⇒ y = b
Slope and area of closed figure remains unchanged under the translation of co-ordinate axes.
Ex.13 Three lines x + 2y + 3 = 0, x + 2y - 7 = 0 and 2x - y - 4 = 0 form 3 sides of two squares. Find the equation of remaining sides of these squares.
Sol.
Distance between the two parallel lines is The equations of sides A and C are of the form 2x – y + k = 0. Since distance between sides A and B = distance between sides
Hence the fourth sides of the two squares are (i) 2x – y + 6 = 0, (ii) 2x – y – 14 = 0
Ex.14 Find the foot of the perpendicular drawn from the point (2, 3) to the line 3x - 4y + 5 = 0. Also, find the image of (2, 3) in the given line.
Sol.
Let AB ≡ 3x – 4y + 5 = 0, P ≡ (2, 3) and PM ⊥ AB .
Slope of AB = 3/4
slope of PM = -4/3 = tanθ
Which is the foot of the perpendicular.
Let Q be the image of P
G. Bisectors Of The Angles Between Two Given Lines
Angular bisector is the locus of a point which moves in such a way so that its distance from two intersecting lines remains same.
The equation of the two bisectors of the angles between the lines a1x + b1y + c1 = 0 and
a2 x + b2y + c2 = 0 are .
If the two given lines are not perpendicular i.e. a1 a2 + b1 b2 ¹ 0, then one of these equation is the equation of the bisector of the acute angle and the other that of the obtuse angle.
Note : Whether both lines are perpendicular or not but the angular bisectors of these lines will always be mutually perpendicular.
(1) The bisectors of the acute and the obtuse angles :
Take one of the lines angle let its slope be m1 and take one of the bisectors and let its slope be m2. If q be the acute angle between them, then find tanθ = .
If then the bisector taken is the bisector of the obtuse angle and the other one will be the bisector of the acute angle. If
then the bisector taken is the bisector of the acute angle and the other one will be the bisector of the obtuse angle.
If two lines are a1x + b1y + c1 = 0 and a2x + b2y + c2 = 0 , then will represent the equation of the bisector of the acute or obtuse angle between the lines according as c1c2 (a1a2+ b1b2 ) is negative or positive.
(2) The equation of the bisector of the angle containing the origin
Write the equations of the two lines so that the constants c1 and c2 become positive. Then the equation is the equation of the bisector containing the origin.
Notes :
(i) If , then the origin will lie in the acute angle and if
, then origin will lie in the obtuse angle.
(ii) The note (i) is helpful in finding the equation of bisector of the obtuse angle or acute angle directly.
(3) The equation of the bisector of the angle which contains a given point
The equation of the bisector of the angle between the two lines containing the point is
or
according as
and
are of the same sings or of opposite signs.
Ex.15 For the straight line and
, find the equation of the
(i) bisector of the obtuse angle between them.
(ii) bisector of the actus angle between them.
(iii) bisector of the angle which contains (1, 2).
Sol. Equations of bisectors of the angles between the given lines are
and
.
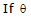 is the acute angle between the line
is the acute angle between the line and the bisector
, then
Hence
(i) The bisector of the obtuse angle is
(ii) The bisector of the acute angle is
(iii) The bisector of the angle containing the origin
(i) For the point (1, 2), 4x + 3y – 6 = 4 × 1 + 3 × 2 – 6 > 0 ⇒ 5x + 12y + 9 = 5 × 1 + 12 × 2 + 9 > 0
Hence equation of the bisector of the angle containing the point (1, 2) is
Alternative : 5 lines. Similarly bisector of obtuse angle is 9x - 7y - 41 = 0.
(4) The equation of reflected ray :
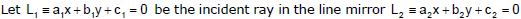
Let L3 be the reflected ray from the line L2. Clearly L2 will be one of the bisectors of the angles between L1 and L3. Since L3 passes through A, 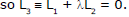
Let (h, k) be a point on L2. Then
Note : Some times the reflected ray L3 is also called the mirror image of L1 in L2.
H. Family of Lines
The general equation of the family of lines through the point of intersection of two given lines is
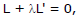 where L = 0 and L' = 0 are the two given lines, and
where L = 0 and L' = 0 are the two given lines, and 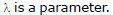 Conversely, any line of the form
Conversely, any line of the form  passes through a fixed point which is the point of intersection of the lines
passes through a fixed point which is the point of intersection of the lines
L1 = 0 and L2 = 0.
The family of lines perpendicular to a given line ax + by + c = 0 is given by bx - ay + k = 0, where k is a parameter.
The family of lines parallel to a given line ax + by + c = 0 is given by ax + by + k = 0, where k is a parameter.
Ex.16 Show that all the chords of the curve 3x2 - y2 - 2x + 4y = 0, which subtend a right angle at the origin pass through a fixed point. Find that the point.
Sol. Let the equation of chord be lx + my = 1. So equation of pair of straight line joining origin to the points of intersection of chord and curve.
3x2 – y2 – 2x (lx + my) + 4y(l + my) = 0, which subtends right angle at origin.
⇒ (3 – 2l + 4m – 1) = 0 ⇒ 1 = 2m + 1. Hence chord becomes (2m + 1)x + my = 1
x – 1 + m(2x + y) = 0
Which will pass through point of intersection of L1 = 0 and L2 = 0.
⇒ x = 1, y = – 2. Hence fixed point is (1, – 2).
(1) One Parameter Family of Straight Lines
If a linear expression L1 contains an unknown coefficient, then the line L1 = 0 can not be a fixed line. Rather it represents a family of straight lines known as one parameter family of straight lines. e.g. family of lines parallel to the x-axis i.e. y = c and family of straight lines passing through the origin i.e. y = mx.
Each member of the family passes a fixed point. We have two methods to find the fixed point.
Method (i) :
Let the family of straight lines of the form ax + by + c = 0 where a, b, c are variable parameters satisfying the condition al + bm + cn = 0, where I, m, n, are given and n ¹ 0. Rewriting the condition as a 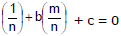 and comparing with the given family of straight lines, we find that each member of it passes through the fixed point
and comparing with the given family of straight lines, we find that each member of it passes through the fixed point
Ex.17 If the algebraic sum of perpendiculars from n given points on a variable straight line is zero then prove that the variable straight line passes through a fixed point.
Sol. Let n given points be (x1, y1) where i = 1, 2 .......... n and the variable line is ax + by + c = 0, Given that
Hence the variable straight line always passes through the fixed point .
Method (ii) :
If a family of straight lines can be written as 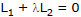 where L1, L2 are two fixed lines and
where L1, L2 are two fixed lines and 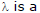 parameter, then each member of it will pass through a fixed point given by point of intersection of L1 = 0 and L2 = 0.
parameter, then each member of it will pass through a fixed point given by point of intersection of L1 = 0 and L2 = 0.
Note : If L1= 0 an L2 = 0 are parallel lines, they will meet at infinity.
Ex.18 Prove that each member of the family of straight lines
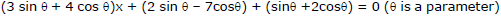 passes through a fixed point.
passes through a fixed point.
Sol. The given family of straight lines can be rewritten as (3x + 2y + 1) sinθ +(4x - 7y + 2) cosθ = 0
or, (4x - 7y + 2) + tanθ (3x + 2y + 1) = 0 which is of the form 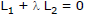
Hence each member of it will pass through a fixed point which is the intersection of 4x - 7y + 2 = 0 and
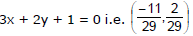
(2) Concurrency of Straight Lines : The condition for 3 lines a1x + b1y + c1 = 0, a2x + b2 + c2 = 0, a3x + b3x + b3y + c3 = 0 to be concurrent is
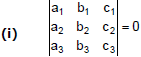
(ii) There exist 3 constants l, m, n (not all zero at the same time) such that L1 + mL2 + nL3 = 0, where L1 = 0, L2 = 0 and L3 = 0 are the three given straight lines.
(iii) the three lines are concurrent if any one of the lines passes through the pint of intersection of the other two lines.
I. Pair of Straight lines
The combined equation of pair of straight lines L1 = a1x + b1y + c1 = 0 and L2 = a2x + b2y + c2 = 0 is (a1x + b1y + c1) (a2x + b2y + c2) = 0 i.e. L1L2 = 0. Opening the brackets and comparing the terms with the terms of general equation of 2nd degree ax2 + 2hxy + by2 + 2gx + 2fy + c = 0, we can get all the following results for a pair of straight lines.
The general equation of second degree ax2 + 2hxy + by2 + 2gx + 2fy + c = 0 represents a pair of straight and h2 ≥ ab.
⇒ abc + 2fgh – al2 – bg2 – ch2 = 0 and h2 ≥ ab.
The homogeneous second degree equation ax2 + 2hxy + by2 = 0 represents a pair of straight lines through the origin if 
If the lines through the origin whose joint equation is ax2 + 2hxy + by2 = 0, are y = m1x and
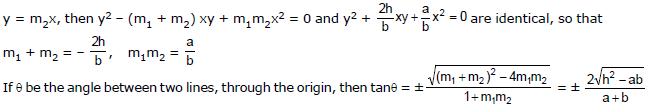
The lines are perpendicular if a + b = 0 and coincident if h2 = ab.
In the more general case, the lines represented by ax2 + 2hxy + by2 + 2gx + 2fy + c = 0 will be perpendicular if a + b = 0, parallel if the terms of second degree make a perfect square i.e. ax2 + 2hxy + by2 gets converted into (l1x + 2hxy + by2 gets converted into (l1x ± m1y)2, coincident if the whole equation makes a perfect square i.e. ax2 + 2hxy + by2 + 2fy + c can be written as (lx + my + n)2.
Note : Point of intersection of the two lines represented by ax2 + 2hxy + by2 + 2gx + 2fy +c = 0 is 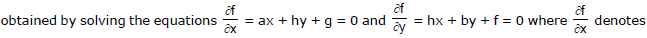
the derivative of f with respect to y, keeping x constant. The fact can be used in splitting ax2 + by2 + 2hxy + 2gx + 2fy + c = 0 into equations of two straight lines. With the above method, the point of intersection can be found. Now only the slopes need to be determined.
If should be noted that the line ax + hy + g = 0 and hx + by + f = 0 are not the lines represented by ax2 + 2hxy + by2 + 2gx + 2fy + c = 0. These are the lines concurrent with the lines represented by given equation.
(Homogenization) Joint equation of pair of lines joining the origin and the points of intersection of a curve and a line :
If the line lx + my + n = 0, ((n # 0) i.e. the line does not pass through origin) cuts the curve ax2 + 2hxy + by2 + 2gx + 2fy + c = 0 at two points A and B, then the joint equation of straight lines passing through A and B and the origin is given by homogenizing the equation of the curve by the equation of the line. i.e.
is the equation of the line OA and OB
Ex.19 If the lines ax + y + 1 = 0, x + by + 1 = 0 and x + y + c = 0(a, b and c being distinct and different from 1) are concurrent, then prove that = 1.
Sol.
Since the given lines are concurrent
Operating C2 → C2 – C1 and C3 → C3 – C1 , we get
a (b – 1) (c – 1) – (b – 1) (1 – a) –(c – 1) (1 – 0) = 0
Ex.20 The chord √6 y = √8 ρx + √2 of the curve ρy2 + 1 = 4x subtends a right angle at origin then find the value ofρ.
Sol.
√3 y - 2ρx = 1 is the given chord. Homogenizing the equation of the curve, we get,
ρy2 – 4x( 3 y – 2ρx) + (√ 3 y – 2ρx)2 = 0
(4ρ2 + 8ρ)x2 + (ρ + 3)y2 - 4√ 3 xy - 4√ 3 ρxy = 0
Now, angle at origin is 90º
coefficient of x2 + coefficient of y2 =
4ρ2 + 8ρ + ρ + 3 = 0
4ρ2 + ρ+ 3 = 0
=
|
73 videos|264 docs|91 tests
|
FAQs on Distance of a Point from a Line and Distance between two Parallel Lines - Mathematics (Maths) Class 11 - Commerce
| 1. What is the formula to find the distance of a point from a line? |  |
| 2. How do you calculate the distance between two parallel lines? |  |
| 3. Can the distance of a point from a line be negative? |  |
| 4. What does it mean if the distance between two parallel lines is zero? |  |
| 5. How can I find the shortest distance between a point and a line segment? |  |





















