Arithmetico Geometric Series and Harmonic Series | Applied Mathematics for Class 11 - Commerce PDF Download
D. Arithmetico-Geometric Series
A series each term of which is formed by multiplying the corresponding term of an AP & GP is called the Arithmetico-Geometric Series . e.g. 1 + 3x + 5x2 + 7x3 + .....
Here 1, 3, 5, .... are in AP & 1, x, x2, x3 ..... are in GP .
Sum of n terms of an Arithmetico-Geometric Series
Let Sn = a + (a + d) r + (a + 2 d) r² + ..... + [a + (n - 1)d] rn-1
then Sn = ,
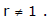
Sum To Infinity : If |r| < 1 & n → ∞ then
rn = 0 . S∞ =
.
Ex.25 Find the sum to n terms of the series
Also find the sum if it exist if n → ∞.
Sol. S = ....(1)
=
....(2)
=
= -
=
Sn = 2 =
.
If n → ∞ then S∞ = = 2
Ex.26 If positive square root of, ..... ∞ is
, find the value of ' a '.
Sol. .
=
now =
and =
( use A G P)
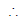
=
= . 23 ⇒
a =
E. Harmonic Progression (HP)
A sequence is said to HP if the reciprocals of its terms are in AP .
If the sequence a1, a2, a3, .... , an is an HP then 1/a1, 1/a2, .... , 1/an is an AP & converse. Here we do not have the formula for the sum of the n terms of an HP . For HP whose first term is a & second term is b, the nth term is tn = . If a, b, c are in HP
⇒ b = or
=
.
Ex.27 If a, b, c are in H.P. then prove that a3b3 + b3c3 + c3a3 = (9 ac - 6 b2) a2c2 .
Sol. =
⇒
- = 0 .
Use p + q + r = 0 ⇒ p3 + q3 + r3 = 3 pqr
Ex.28 If prove that a, b, c are in HP unless b = a + c.
Sol. ⇒ 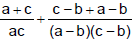 = 0
= 0
⇒ = 0
Let a + c = λ 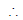
+
= 0
⇒ = 0
acλ – bλ2 + b2λ + acλ - 2abc = 0
⇒ 2ac(λ - b) - bλ (λ - b) = 0
⇒ (2ac - bλ) (λ - b) = 0
⇒a, b, c are in H.P. or a + c = b.
Ex.29 The value of x y z is 55 or 354/55 according as the series a, x, y, z, b is an A.P. or H.P. Find the values of a & b given that they are positive integers.
Sol.
Let a, x, y, z, b are in A.P. ⇒ b = a + 4 d
⇒ d = b-a/4
Similarly when a, x, y, z, b are in H.P.
In the 1st case
In the 2nd case
dividing a3 b3 = 73 ⇒ a = 7 ; b = 1 or a = 1 ; b = 7
|
83 videos|102 docs|62 tests
|
FAQs on Arithmetico Geometric Series and Harmonic Series - Applied Mathematics for Class 11 - Commerce
| 1. What is an arithmetico-geometric series? |  |
| 2. How can we determine the sum of an arithmetico-geometric series? |  |
| 3. What is a harmonic series? |  |
| 4. How can we determine the sum of a harmonic series? |  |
| 5. What are the applications of arithmetico-geometric series and harmonic series in real life? |  |
















