2nd & 3d Law: Entropy Change & Spontaneity | Chemistry Class 11 - NEET PDF Download
Second Law Of Thermodynamics
The second law of thermodynamics put restrictions upon the direction of heat transfer and achievable efficiencies of heat engines. The first law of thermodynamics states that the energy of the universe remains constant, though energy can be exchanged between system and surroundings, it can’t be created or destroyed.
While the first law of thermodynamics gives information about the quantity of energy transfer is a process, it fails to provide any insights about the direction of energy transfer and the quality of the energy. The first law cannot indicate whether a metallic bar of uniform temperature can spontaneously become warmer at one end and cooler at others. All that the law can state is that there will always be energy balance if the process occurs.
It is the second law of thermodynamics that provides the criterion for the feasibility of any process. A process cannot occur unless it satisfies both the first and second laws of thermodynamics.
What is the Second Law of Thermodynamics?
The second law of thermodynamics states that any spontaneously occurring process will always lead to an escalation in the entropy (S) of the universe. In simple words, the law explains that an isolated system’s entropy will never decrease over time.
Nonetheless, in some cases where the system is in thermodynamic equilibrium or going through a reversible process, the total entropy of a system and its surroundings remains constant. The second law is also known as the Law of Increased Entropy.
Second Law of Thermodynamics Equation
Mathematically, the second law of thermodynamics is represented as;
ΔSuniv > 0
where ΔSuniv is the change in the entropy of the universe.
Entropy is a measure of the randomness of the system or it is the measure of energy or chaos within an isolated system. It can be considered as a quantitative index that describes the quality of energy.
Meanwhile, there are few factors that cause an increase in entropy of the closed system. Firstly, in a closed system, while the mass remains constant there is an exchange of heat with the surroundings. This change in the heat content creates a disturbance in the system thereby increasing the entropy of the system.
Secondly, internal changes may occur in the movements of the molecules of the system. This leads to disturbances which further causes irreversibilities inside the system resulting in the increment of its entropy.
Different Statements of The Law
here are two statements on the second law of thermodynamics which are;
- Kelvin- Plank Statement
- Clausius Statement
- Kelvin-Planck Statement
It is impossible for a heat engine to produce a network in a complete cycle if it exchanges heat only with bodies at a single fixed temperature.
Exceptions:
If Q2 = 0 (i.e., Wnet = Q1, or efficiency = 1.00), the heat engine produces work in a complete cycle by exchanging heat with only one reservoir, thus violating the Kelvin-Planck statement. - Clausius’s Statement
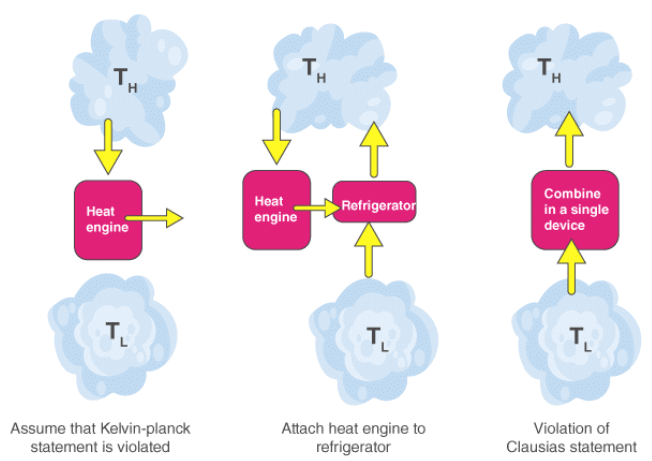
It is impossible to construct a device operating in a cycle that can transfer heat from a colder body to warmer without consuming any work. In other words, unless the compressor is driven by an external source, the refrigerator won’t be able to operate. Heat pump and Refrigerator works on Clausius’s statement.
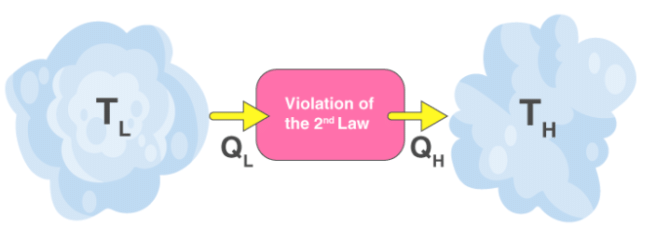 Both Clausius’s and Kelvin’s statements are equivalent i.e a device violating Clausius’s statement will also violate Kelvin’s statement and vice versa.
Both Clausius’s and Kelvin’s statements are equivalent i.e a device violating Clausius’s statement will also violate Kelvin’s statement and vice versa.
 In addition to these statements, a French physicist named Nicolas Léonard Sadi Carnot also known as”father of thermodynamics,” basically introduced the Second Law of Thermodynamics. However, as per his statement, he emphasized the use of caloric theory for the description of the law. Caloric (self repellent fluid) relates to heat and Carnot observed that some caloric was lost in the motion cycle.
In addition to these statements, a French physicist named Nicolas Léonard Sadi Carnot also known as”father of thermodynamics,” basically introduced the Second Law of Thermodynamics. However, as per his statement, he emphasized the use of caloric theory for the description of the law. Caloric (self repellent fluid) relates to heat and Carnot observed that some caloric was lost in the motion cycle.
Perpetual Motion Machine of the Second Kind (PMM2)
The device that produces work while interacting with a single heat reservoir is known as a perpetual motion machine of the second kind (PMM2). Also, a device that violates the second law of thermodynamics is a perpetual motion machine of the second kind.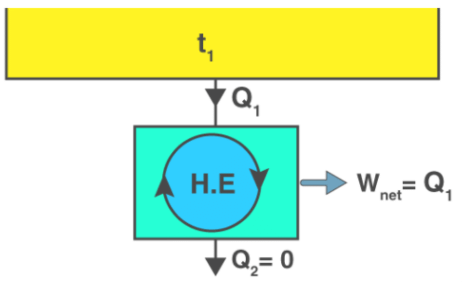 Thus, a heat engine has to interact with at least two thermal reservoirs at different temperatures to produce work in a cycle. So long as there is a difference in temperature, motive power (i.e., work) can be produced. If the bodies with which the heat engine exchange heat are of finite heat capacities, work will be produced by the heat engine until the temperature of the two bodies is equalised.
Thus, a heat engine has to interact with at least two thermal reservoirs at different temperatures to produce work in a cycle. So long as there is a difference in temperature, motive power (i.e., work) can be produced. If the bodies with which the heat engine exchange heat are of finite heat capacities, work will be produced by the heat engine until the temperature of the two bodies is equalised.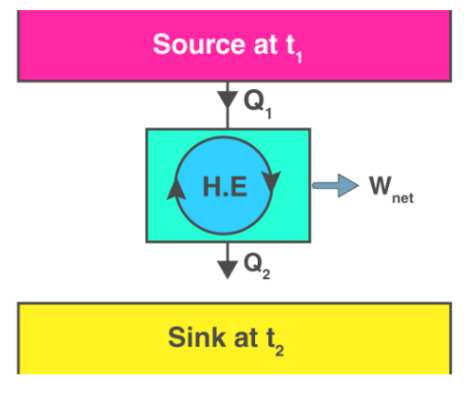
Solved Examples of Second Law Of Thermodynamics
Example 1: A heat pump uses 300 J of work to remove 400 J of heat from the low-temperature reservoir. How much heat is delivered to a higher temperature reservoir?
Solution: W = 300 J
QC = 400 J
QH = W + QC
QH = 300 J + 400 J
QH = 700 J
Heat delivered to the higher temperature reservoir is 700 J.
Example 2: A reversible heat engine receives 4000 KJ of heat from a constant temperature source at 600 K. If the surrounding is at 300K then determine (a) the availability of heat energy (b) unavailable heat.
Solution: Q1 = 4000 KJ
T1 = 600K
T0 = 300 K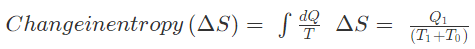
Change in entropy = 4.44 KJ/K
The availability of heat energy,
A = Q1 – T0(ΔS)
A = 4000 – 300(4.44)
A = 2,668 KJ.
Unavailable heat (U.A) = T0 (ΔS)
(U.A) = 300 (4.44)
(U.A) = 1332 KJ.
(a) the availability of heat energy (A) = 2668 KJ
(b) Unavailable heat (U.A) = 1332 KJ.
Third Law Of Thermodynamics
The third law of thermodynamics states that the entropy of a perfect crystal at a temperature of zero Kelvin (absolute zero) is equal to zero.
Entropy, denoted by ‘S’, is a measure of the disorder/randomness in a closed system. It is directly related to the number of microstates (a fixed microscopic state that can be occupied by a system) accessible by the system, i.e. the greater the number of microstates the closed system can occupy, the greater its entropy. The microstate in which the energy of the system is at its minimum is called the ground state of the system.
At a temperature of zero Kelvin, the following phenomena can be observed in a closed system:
- The system does not contain any heat.
- All the atoms and molecules in the system are at their lowest energy points.
Therefore, a system at absolute zero has only one accessible microstate – it’s ground state. As per the third law of thermodynamics, the entropy of such a system is exactly zero. This law was developed by the German chemist Walther Nernst between the years 1906 and 1912.
This law was developed by the German chemist Walther Nernst between the years 1906 and 1912.
Alternate Statements of the 3rd Law of Thermodynamics
The Nernst statement of the third law of thermodynamics implies that it is not possible for a process to bring the entropy of a given system to zero in a finite number of operations.
The American physical chemists Merle Randall and Gilbert Lewis stated this law differently: when the entropy of each and every element (in their perfectly crystalline states) is taken as 0 at absolute zero temperature, the entropy of every substance must have a positive, finite value. However, the entropy at absolute zero can be equal to zero, as is the case when a perfect crystal is considered.
The Nernst-Simon statement of the 3rd law of thermodynamics can be written as: for a condensed system undergoing an isothermal process that is reversible in nature, the associated entropy change approaches zero as the associated temperature approaches zero.
Another implication of the third law of thermodynamics is: the exchange of energy between two thermodynamic systems (whose composite constitutes an isolated system) is bounded.
Why is it Impossible to Achieve a Temperature of Zero Kelvin?
For an isentropic process that reduces the temperature of some substance by modifying some parameter X to bring about a change from ‘X2’ to ‘X1’, an infinite number of steps must be performed in order to cool the substance to zero Kelvin.
This is because the third law of thermodynamics states that the entropy change at absolute zero temperatures is zero. The entropy v/s temperature graph for any isentropic process attempting to cool a substance to absolute zero is illustrated below.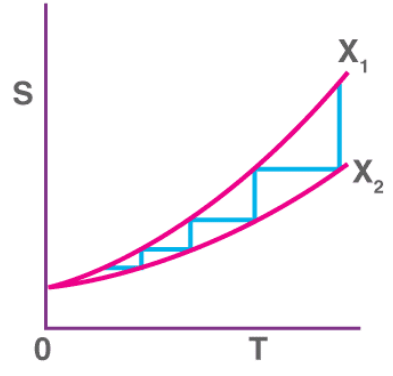 From the graph, it can be observed that – the lower the temperature associated with the substance, the greater the number of steps required to cool the substance further. As the temperature approaches zero kelvin, the number of steps required to cool the substance further approaches infinity.
From the graph, it can be observed that – the lower the temperature associated with the substance, the greater the number of steps required to cool the substance further. As the temperature approaches zero kelvin, the number of steps required to cool the substance further approaches infinity.
Mathematical Explanation of the Third Law
As per statistical mechanics, the entropy of a system can be expressed via the following equation:
S – S0 = 𝑘B ln𝛀
Where,
- S is the entropy of the system.
- S0 is the initial entropy.
- 𝑘B denotes the Boltzmann constant.
- 𝛀 refers to the total number of microstates that are consistent with the system’s macroscopic configuration.
Now, for a perfect crystal that has exactly one unique ground state, 𝛀 = 1. Therefore, the equation can be rewritten as follows:
S – S0 = 𝑘B ln(1) = 0 [because ln(1) = 0]
When the initial entropy of the system is selected as zero, the following value of ‘S’ can be obtained:
S – 0 = 0 ⇒ S = 0
Thus, the entropy of a perfect crystal at absolute zero is zero.
Applications of the Third Law of Thermodynamics
An important application of the third law of thermodynamics is that it helps in the calculation of the absolute entropy of a substance at any temperature ‘T’. These determinations are based on the heat capacity measurements of the substance. For any solid, let S0 be the entropy at 0 K and S be the entropy at T K, then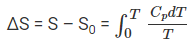
According to the third law of thermodynamics, S0 = 0 at 0 K,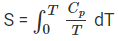
The value of this integral can be obtained by plotting the graph of Cp / T versus T and then finding the area of this curve from 0 to T. The simplified expression for the absolute entropy of a solid at temperature T is as follows: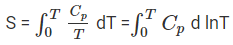
= Cp ln T = 2.303 Cp log T
Here Cp is the heat capacity of the substance at constant pressure and this value is assumed to be constant in the range of 0 to T K.
Entropy
Entropy is one of the important concepts that students need to understand clearly while studying Chemistry and Physics. More significantly, entropy can be defined in several ways and thus can be applied in various stages or instances such as in a thermodynamic stage, cosmology, and even in economics.
The concept of entropy basically talks about the spontaneous changes that occur in the everyday phenomenon or the tendency of the universe towards disorder.
What is Entropy?
Generally, entropy is defined as a measure of randomness or disorder of a system. This concept was introduced by a German physicist named Rudolf Clausius in the year 1850.
Apart from the general definition, there are several definitions that one can find for this concept. The two definitions of entropy that we will look here are the thermodynamic definition and the statistical definition.
From a thermodynamics viewpoint of entropy, we do not consider the microscopic details of a system. Instead, entropy is used to describe the behaviour of a system in terms of thermodynamic properties such as temperature, pressure, entropy, and heat capacity. This thermodynamic description took into consideration the state of equilibrium of the systems.
Meanwhile, the statistical definition which was developed at a later stage focused on the thermodynamic properties which were defined in terms of the statistics of the molecular motions of a system. Entropy is a measure of the molecular disorder.
Properties of Entropy
- It is a thermodynamic function.
- It is a state function. It depends on the state of the system and not the path that is followed.
- It is represented by S but in the standard state, it is represented by S°.
- It’s SI unit is J/Kmol.
- It’s CGS unit is cal/Kmol.
- Entropy is an extensive property which means that it scales with the size or extent of a system.
Note: The greater disorder will be seen in an isolated system, hence entropy also increases. When chemical reactions take place if reactants break into more number of products, entropy also gets increased. A system at higher temperatures has greater randomness than a system at a lower temperature. From these examples, it is clear that entropy increases with a decrease in regularity.
Entropy order: gas > liquid > solids
Entropy Change and Calculations
During entropy change, a process is defined as the amount of heat emitted or absorbed isothermally and reversibly divided by the absolute temperature. Entropy formula is given as;
∆S = qrev,iso / T
If we add the same quantity of heat at a higher temperature and lower temperature, randomness will be maximum at a lower temperature. Hence, it suggests that temperature is inversely proportional to the entropy.
Total entropy change, ∆Stotal = ∆Ssurroundings + ∆Ssystem
Total entropy change is equal to the sum of entropy change of system and surroundings.
If the system loses an amount of heat q at a temperature T1, which is received by surroundings at a temperature T2.
So, ∆Stotal can be calculated
∆Ssystem = -q/T1
∆Ssurrounding = q/T2
∆Stotal = -q/T1 + q/T2
- If ∆Stotal is positive, the process is spontaneous.
- If ∆Stotal is negative, the process is non-spontaneous.
- If ∆Stotal is zero, the process is at equilibrium.
Points To Remember
A spontaneous process is thermodynamically irreversible.
The irreversible process will attain equilibrium after some time.
Entropy change during the isothermal reversible expansion of an ideal gas
∆S = qrev,iso/T
According to the first law of thermodynamics,
∆U = q + w
For the isothermal expansion of an ideal gas, ∆U = 0
qrev = -wrev = nRTln(V2 / V1)
Therefore, ∆S = nRln(V2 / V1)
Entropy Change During Reversible Adiabatic Expansion
For an adiabatic process heat exchange will be zero(q = 0), therefore reversible adiabatic expansion is taking place at a constant entropy (isentropic),
q = 0
Therefore, ∆S = 0
Even though the reversible adiabatic expansion is isentropic, irreversible adiabatic expansion is not isentropic.
∆S not equal to Zero.
Entropy and Thermodynamics
Here we will compare or understand the relationship between entropy and the different laws of thermodynamics.
- First Law of Thermodynamics
- Second Law of Thermodynamics
- Third Law of Thermodynamics
1. First Law of Thermodynamics
It states that heat is a form of energy, and thermodynamic processes are therefore subject to the principle of conservation of energy. This means that heat energy cannot be created or destroyed. It can, however, be transferred from one place to another and converted to and from other forms of energy.
Note:
- Entropy increases when solid changes to a liquid and liquid change into gases.
- Entropy also increases when the number of moles of gaseous products increases more than the reactants.
Some things contrary to expectations about entropy.
- A hard-boiled egg has greater entropy than an unboiled egg. It is due to the denaturation of the secondary structure of the protein (albumin). Protein changes from the helical structure into a random coiled form.
- If we stretch a rubber band entropy get decreased because macromolecules get uncoiled and arranged in a more ordered manner. Therefore randomness will decrease.
2. Second Law of Thermodynamics
According to concepts of entropy and spontaneity, the second law of thermodynamics has a number of definitions.
- All naturally occurring spontaneous processes are thermodynamically irreversible
- Complete transmission of heat into work is thermodynamically not feasible without wastage of a certain amount of energy
- The entropy of the universe is continuously increasing
- Total entropy change is always positive. The entropy of a system plus the entropy of surrounding will be greater than zero.
∆Stotal = ∆Ssurroundings + ∆Ssystem > 0
3. Third Law of Thermodynamics
The entropy of any crystalline solid approaches zero as the temperature approaches absolute temperature. It is because there is a perfect order in a crystal at absolute zero
The limitation of this law is that many solids do not have zero entropy at absolute zero.
Example: glassy solid, solid containing a mixture of isotopes.
Entropy Changes During Phase Transition
- Entropy of Fusion
It is the increase in entropy when a solid melt into liquid. The entropy increases as the freedom of movement of molecules increase with phase change.
The entropy of fusion is equal to the enthalpy of fusion divided by melting point(fusion temperature)
∆fusS = ∆fusH / Tf
A natural process such as a phase transition (eg. fusion) will occur when the associated change in the Gibbs free energy is negative.
Most of the time ∆fusS is positive
Exception: Helium-3 has a negative entropy of fusion at temperatures below 0.3 K. Helium-4 also has a very slightly negative entropy of fusion below 0.8 K. - Entropy of Vaporization
The entropy of vaporization is a state when there is an increase in entropy as liquid changes into a vapour. This is due to an increase in molecular movement which creates a randomness of motion.
The entropy of vaporization is equal to the enthalpy of vaporization divided by boiling point. It can be represented as;
∆vapS = ∆vapH / T
Standard Entropy of Formation of a Compound
It is the entropy change that takes place when one mole of a compound in the standard state is formed from the elements in the standard state.
Spontaneity
- Exothermic reactions are spontaneous because ∆Ssurrounding is positive which make ∆Stotal positive.
- Endothermic reactions are spontaneous because ∆Ssystem is positive and ∆Ssurroundings is negative but overall ∆Stotal is positive.
- Free energy change criteria for predicting spontaneity is better than entropy change criteria because the former requires only free energy change of system whereas the latter needs entropy change of both system and surroundings.
Negentropy
It is a reverse of entropy. It means things becoming more in order. By ‘order’ it means organisation, structure and function. It is the opposite of randomness or chaos.
One example of negentropy is a star system such as a solar system.
Solved Questions
Q.1. The entropy of an isolated system can never ____?
(a) increase
(b) decrease
(c) be zero
(d) none of the mentioned
Ans: b
Explanation: The entropy of an isolated system always increases and remains constant only when the process is reversible.
Q.2. According to the entropy principle, the entropy of an isolated system can never decrease and remains constant only when the process is reversible?
(a) true
(b) false
Ans: a
Explanation: This is the statement for the principle of increase of entropy.
Q.3. Entropy may decrease locally in some region within the isolated system. How can this statement be justified?
(a) this cannot be possible
(b) this is possible because the entropy of an isolated system can decrease
(c) it must be compensated by a greater increase of entropy somewhere within the system.
(d) none of the mentioned
Ans: c
Explanation: The net effect of an irreversible process is an entropy increase of the whole system.
Q.4. Clausius summarized the first and second laws of thermodynamics as?
(a) the energy of the world is constant
(b) the entropy of the world tends towards a maximum
(c) both of the mentioned
(d) none of the mentioned
Ans: c
Explanation: These two statements were given by Clausius.
Q.5. The entropy of an isolated system always ____ and becomes a ____ at the state of equilibrium?
(a) decreases, minimum
(b) increases, maximum
(c) increases, minimum
(d) decreases, maximum
Ans: b
Explanation: If the entropy of an isolated system varies with some parameter, then there is a certain value of that parameter that maximizes the entropy.
|
114 videos|263 docs|74 tests
|
FAQs on 2nd & 3d Law: Entropy Change & Spontaneity - Chemistry Class 11 - NEET
| 1. What is entropy and how does it relate to entropy change in a system? |  |
| 2. What factors affect the entropy change in a system? |  |
| 3. How can we determine the spontaneity of a process based on entropy change? |  |
| 4. Can entropy decrease in a system? |  |
| 5. How does the concept of entropy relate to everyday life? |  |

















