Carnot Cycle & Gibbs Energy Change | Physical Chemistry for NEET PDF Download
CARNOT CYCLE
Carnot cycle is based on 4 reversible process.
(1) Reversible isothermal expansion from A to B.
ΔEAB = 0 ,
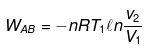
(2) Reversible adiabatic expansion from B to C
ΔEBC = nCV(T2 -T1)
WBC = ΔEBC
(3) Isothermal compression from C to D
ΔECD = 0,
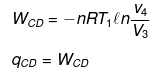
(4) Adiabatic compression from D to A.
ΔEDA = nCV(T1 - T2)
WDA = ΔEDA
ΔECycle = 0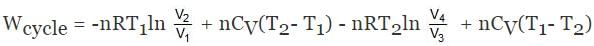
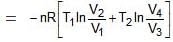
For BC,
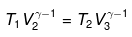
For ΔA,
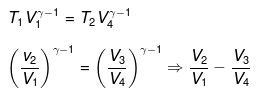
Wcycle = -nR(T1 - T2)ln V2/V1
Efficiency of any engine may be given as
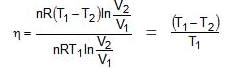
ΔEcycle = qcyc wcycle
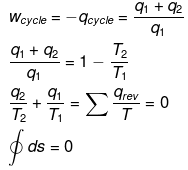
This means ΔS is a state function
Gibb's Free Energy (G)
Gsystem = Hsystem - TSsystem
W = Wexpansion +Wnon-expansion
Wnon - expansion = wuseful (useful work)
ΔG = Wnon expansion = Wuseful
All those energy which is available with the system which is utilized in doing useful work is called Gibb's free energy :
Rx :
1. ΔGsystem = ΔHsystem - TΔSsystem = - TΔSuniverse = Wnon expansion = Wuseful
2. ΔGsystem = - TΔSuniverse
3.
(a) ΔSuniverse > 0 or ΔGsystem < 0 ⇒ Spontaneous
(b) ΔSuniverse = 0 or ΔGsystem = 0 ⇒ Equilibrium
(c) ΔSuniverse < 0 or ΔGsystem > 0 ⇒ Non-Spontaneous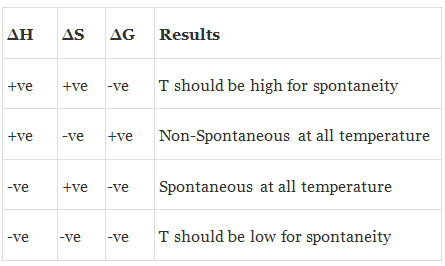
APPLICATION OF ( ΔG )
Rx :
(1) aA + bB ⇌ cC + dD
ΔG° = Standard Gibb's free energy change (P = 1 atm, 298 K)
ΔG = Gibb's free energy change at any condition.
NERNST EQUATION
ΔG = ΔG° + 2.303 RT log Q ; Q = Reaction Quotient
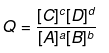
At equilibrium, ΔG = 0 and Q = Keq.
0 = ΔG° 2.303 RT log keq
ΔG° = -2.303 RT log keq
å G°(product) - å G° (Reactant) = - 2.303 RT log keq
ΔH° - T ΔS° = -2.303 RT log keq
(2) Wcell = q × E
ΔG = - Wcell
ΔG = - q × Ecell
Now, one mole e- have charge 96500 coulomb = 1 Faraday (F)
n mole of e- will have charge = n × F or q = n × F
ΔG = - nFEcell
ΔG° = -nFE°cell
THIRD LAW OF THERMODYNAMICS
limitT→0 S = 0
Third law of thermodynamics states that as the temperature approaches absolute zero, the entropy of perfectly crystalline substance also approaches zero.
APPLICATION OF THIRD LAW OF THERMODYNAMICS
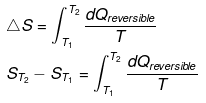
Taking T2 = T and T1 = 0°k.
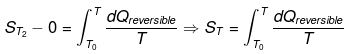
For perfectly crystalline substance. The entropy of perfectly crystalline substance can be determined using third law of thermodynamics.
or
With the help of third law of thermodynamics we can calculate the exact value of entropy.
ΔG AND NON PV WORK (NON EXPANSION/COMPRESSION)
(ΔG)T,P is a measure of useful work a non PV work (non expansion work) that can be produced by a chemical transformation.e.g.electrical work .
For reversible reaction at constant T & P
dU = dq + dWtotal
dU = dq + dWP, V + dWnon P,V
dU = T.dS - P. dV + dWnon P,V
dU + P.dV = T. dS + dWnon P,V
dH = T.dS + dWnon P,V
(dGsys)T,P = dWnon P,V
Useful work done on the system = increase in Gibb's energy of system at constant T & P.
- (ΔGsys)T,P= - Wnon P,V
- (ΔGsys)T,P= - Wby, non P,V
Useful work done by the system = decrease in Gibb's energy of system at constant T & P.
If (ΔGsys)T,P = 0, then system is unable to deliver useful work.
THERMODYNAMIC RELATION
For reversible process in which non-expansion work is not possible
dU = dq + dW
H = U + PV
dH = dU + P.dV + VdP
dH = T.dS - PdV + PdV + V.dP
dH = T.dS + V.dP
G = H -TS
dG = dH - T.dS -S.dT
dG = T.dS + V.dP - T.dS - S.dT
For a particular system (s/ℓ/g)
(1) At constant temperature dG = V.dP
or
(A) For a system is s/ ℓ phase
(B) For an ideal gas, expansion/compression:-
(2) At constant pressure : dG =-S.dT
or
For phase transformation/chemical reaction
d(ΔG) = ΔV.dP - ΔS dT
H2O(s) → H2O(l)
ΔV = VM(H2O,l) - Vm(H2O,s)
ΔS = SM(H2O,l) - Sm(H2O,s)
A(s) → B(g) + 2C(g)
ΔrS = SM(B,g ) 2Sm(C,g) - Sm(A,s)
C (s, graphite) → C(s, diamond)
ΔV = Vm(C, diamond) - Vm(C-graphite)
At constant temperature:-
d(ΔG) = ΔV. dP
At constant pressure
ΔrGT2 - ΔrGT1 = - ΔrS(T2 - T1)
GIBBS FREE ENERGY
Another thermodynamic quantities that helps in predicting the spontaneity of a process is Gibbs free energy or Gibbs energy of Gibbs function.
It is denoted by G and is given by the equation
G = H -TS
where H is the heat content, T is the absolute temperature and S is the entropy of the system.
G1 = H1 -TS1 for the initial state
G2 = H2 -TS2 for the final state
G2 -G1 = (H2 -H1) -T (S2 -S1)
ΔG = ΔH -TΔS
ΔG = G2 -G1 is the change in Gibbs free energy of the system
ΔH = H2 -H1 is the enthalpy change of the system
ΔS = S2 -S1 is the entropy change of the system.
ΔG = ΔH -TΔS is known as Gibbs – Helmoholtz equation.
Gibbs free energy is that thermodynamic quantity of a system the decrease in whose value during a process is equal to the maximum possible useful work that can be obtained from the system.
The relationship between heat absorbed by a system q, the change in its internal energy , ΔU , and the work done by the system is given by the equation of the first law of thermodynamics i.e.
q = ΔU + wexpansion + wnon-expansion
Under constant pressure conditions , the expansion work is given by PΔV.
q = ΔU + PΔV + wnon-expansion
q = ΔH + wnon-expansion
For a reversible change taking place at constant temperature ,
ΔS = qrev /T
qrev =TΔS
TΔS = ΔH + wnon-expansion
ΔH – TΔS = – wnon-expansion
For a change taking place under condition of constant temperature and pressure,
ΔG = ΔH -TΔS
ΔG = – wnon-expansion
Free energy change can be taken as a measure of work other than the work of expansion.
The work of expansion cannot be converted to other useful work ,whereas the non – expansion work is convertible to useful work.
−ΔG = wnon-expansion = wuseful
The decrease in free energy of system during any change, ΔG, is a measure of the useful or net work derived during the change. The free energy, G, of a system is a measure of its capacity to do useful work. It is a part of the energy of the system which is free for conversion to useful work and is therefore called free energy.
The free energy change is equal to the maximum possible useful work that can be obtained from the process. Hence we can write, −ΔG = wmax
The greater the change in Gibbs energy , greater is the amount of work that can be obtained from the process.
If the work involved is the electrical work then as electrical work = nEF , the above relationship is written as:
−ΔG = nEF
where n = number of electrons involved in the cell reaction
E= EMF of the cell
F =Faraday
If all the reactants and products of the cell reaction are in their standard states i.e. 298 K and one atmosphere pressure, the above relation is written as
−ΔG° = nFE°
where ΔG° is the standard free energy change,
ΔG° is the standard EMF of the cell.
In a fuel cell, it is found that the heat evolved is not completely converted into energy i.e. useful work.
The ratio ΔG / ΔH is called the efficiency of the fuel cell.
SPONTANEITY IN TERMS OF FREE ENERGY CHANGE
(1) Deriving the criteria from entropy consideration
The total entropy change when the system is not isolated from the surrounding is given by ΔS = ΔSsystem + ΔSsurrounding
Consider a process being carried out at constant temperature and pressure.
Suppose the heat is lost by the surrounding and gained by the system.If the heat lost by the surrounding is represented by qp then by definition of entropy change
ΔSsurrounding = − qp /T
At constant pressure,
qP = ΔH
ΔSsurrounding = − ΔH /T
ΔStotal = ΔSsystem − ΔH /T
ΔStotal = ΔS − ΔH /T
Multiplying throughout by T ,we get
TΔStotal = TΔS – ΔH
ΔG = ΔH -TΔS
TΔStotal = – ΔG
ΔG = − TΔStotal
(a) If ΔStotal is positive, the process is spontaneous .
(b) If ΔStotal is zero, the process is in equilibrium.
(c) If ΔStotal is negative ,the direct process is non spontaneous, the reverse process may be spontaneous.
The criteria in terms of free energy change for the spontaneity of the process will be as follow:
(i) If ΔG is negative, the process will be spontaneous.
(ii) If ΔG is zero, the process is in equilibrium.
(iii) If ΔG is positive, the direct process is non spontaneous, the reverse process may be spontaneous.
(2) Driving the criteria from Gibbs energy equation
According to Gibbs energy equation,
ΔG = ΔH -TΔS
This equation combines in itself the factors which decides the spontaneity of a process, namely:
(a) the energy factor, ΔH
(b) the entropy factor, TΔS
ΔG is the resultant of energy factor and entropy factor.
Depending upon the signs of ΔH and TΔS and their relative magnitude, the following possibilities arises:
(a) When both ΔH and TΔS are negative i.e. energy factors favours the process but randomness factors opposes it. Then
(i) If ΔH > TΔS the process is spontaneous and ΔG is negative.
(ii) If ΔH < TΔS the process is non spontaneous and ΔG is positive.
(iii) If ΔH = TΔS, the process is in equilibrium and ΔG is zero.
(b) When both ΔH and TΔS are positive i.e. energy factor opposes the process but randomness factor favours it. Then
(i) If ΔH > TΔS the process is non-spontaneous and ΔG is positive.
(ii) If ΔH < TΔS the process is spontaneous and ΔG is negative.
(iii) If ΔH = TΔS, the process is in equilibrium and ΔG is zero.
(c) When ΔH is negative and TΔS is positive i.e. energy factor as well as the randomness factor favour the process. The process will be highly spontaneous and ΔG will be highly negative.
(d) When ΔH is positive but TΔS is negative i.e. energy factor as well as the randomness factor opposes the process. The process will be highly non-spontaneous and ΔG will be highly positive.
(i) If ΔG is negative the process is spontaneous.
(ii) If ΔG is zero, the process does not occur or the system is in equilibrium.
(iii) If ΔG is positive the process does not occur in the forward direction. It may occur in the backward direction.
Effect of temperature on the spontaneity of a process
The spontaneity of a process depends upon
(a) the energy factor
(b) the randomness or entropy factor
The resultant ΔG = ΔH – T ΔS would change with temperature and so would spontaneity of the process.
For endothermic reactions
ΔH is always positive i.e. this factor opposes the process.
(a) If TΔS is negative, this factor will also oppose the process and process will be non spontaneous.
(b) If TΔS is positive then the process can occur if magnitude of the factor TΔS is greater than the magnitude of ΔH. The reaction is then said to be entropy driven. The magnitude of the factor,TΔS is affected by temperature as follow:
(i) If the temperature is very low such that TΔS < ΔH in magnitude, ΔG will be positive and hence the process will be non spontaneous.
(ii) If the temperature is moderate such as TΔS > ΔH slightly in magnitude , ΔG will be slightly negative. Hence the process will be spontaneous but slow.
(iii) If the temperature is high, TΔS will be much greater than ΔH in magnitude so that ΔG is highly negative. Hence the process will not only be spontaneous but fast.
An endothermic reaction which may be non-spontaneous at low temperature may become spontaneous at high temperature.
This is the reason why endothermic reactions are carried out at high temperature.
For exothermic reaction
ΔH is always negative i.e. this factor always favours the process.
If TΔS is positive , this factor will favour the process and the process will always be spontaneous.
If TΔS is negative, then the process can occur only if the magnitude of ΔH is very large so that ΔG is negative. The reaction is then said to be enthalpy driven.
The magnitude of TΔS and hence, the spontaneity of the reaction is affected by temperature as follow :
(i) If the temperature is so high that TΔS > ΔH in magnitude, ΔG will be positive and the process will be non- spontaneous.
(ii) If the temperature is made so low that TΔS < ΔH in magnitude, ΔG will be negative and the process will be spontaneous.
An exothermic reaction which may be non-spontaneous at high temperature may become spontaneous at low temperature.
Standard free energy change of a reaction (ΔG° reaction )and standard free energy of formation(ΔfG°)
Standard free energy change of a reaction is defined as the change in free energy which takes place when the reactants in the standard state are converted into products in their standard state.
The free energy change during a process can be calculated from the standard free energy of formation of the different reactants and products involved, taking standard free energy of formation of elements as zero i.e. for any process or reaction,
ΔrG° = (sum of the standard free energy of formation of products) – ( Sum of the standard free energy of formation of reactants)
ΔrG° = ∑ΔfG°( products) – ∑ΔfG°(Reactants)
Standard free energy of formation of a compound is defined as the free energy change which take place when one mole of the compound is formed from its elements taken in their standard state.
Standard free energy of formation of elementary substances is taken as zero.
|
117 videos|226 docs|237 tests
|
FAQs on Carnot Cycle & Gibbs Energy Change - Physical Chemistry for NEET
| 1. What is a Carnot cycle? |  |
| 2. How does a Carnot cycle work? |  |
| 3. What is the efficiency of a Carnot cycle? |  |
| 4. What are the limitations of the Carnot cycle? |  |
| 5. What are some real-life applications of the Carnot cycle? |  |






















