Commerce Exam > Commerce Notes > Mathematics (Maths) Class 11 > Limits of Trigonometric Functions
Limits of Trigonometric Functions | Mathematics (Maths) Class 11 - Commerce PDF Download
limit of Trigonometric Functions
(a)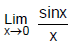 
= 1 (approach from left side)
(b)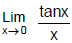 
= 1 (approach from right side)
(c)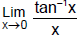
= 1
(d) 
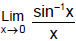= 1
[Where x is measured in radians]
Ex.17 Find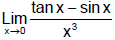 
Sol.
Ex.18 Evaluate :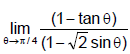 
Sol.
Ex.19 Solve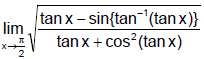 
Sol.
Note : Limit Using Expansion of Functions
Ex.20 Find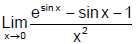 
Sol.
Ex.21 Find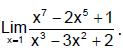 
Sol.
This is of the form 0/0 if we put x = 1. Therefore we put x = 1 + h and expand.
Ex.22 Evaluate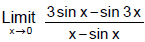 
Sol.
Ex.23 Let f(x) be a function such that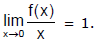 
Find the values of a and b such that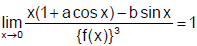 
Sol.
R.H.S. is finite then L.H.S. is also finite, then 1 + a –b = 0 and 
Ex.24 If the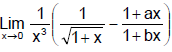 
exists and has the value equal to l, then find the value of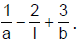 
Sol.
Use binomial expansion to get the following relations :
The document Limits of Trigonometric Functions | Mathematics (Maths) Class 11 - Commerce is a part of the Commerce Course Mathematics (Maths) Class 11.
All you need of Commerce at this link: Commerce
|
75 videos|238 docs|91 tests
|
FAQs on Limits of Trigonometric Functions - Mathematics (Maths) Class 11 - Commerce
| 1. What are the limits of sin(x) and cos(x) as x approaches infinity? |  |
Ans. The limits of sin(x) and cos(x) as x approaches infinity do not exist. Both functions oscillate between -1 and 1 infinitely, without converging to a specific value.
| 2. Can the limit of tan(x) as x approaches infinity be determined? | |
Ans. No, the limit of tan(x) as x approaches infinity does not exist. The tangent function becomes unbounded and oscillates between negative and positive infinity as x approaches infinity.
| 3. What is the limit of sin(x)/x as x approaches 0? | |
Ans. The limit of sin(x)/x as x approaches 0 is 1. This result is known as the Squeeze Theorem or the Fundamental Theorem of Calculus.
| 4. Are there any limits for the cotangent function? | |
Ans. Yes, the limit of cot(x) as x approaches 0 is infinity, and the limit of cot(x) as x approaches infinity is 0. These limits can be derived using the reciprocal properties of the cotangent function.
| 5. What is the limit of sec(x) as x approaches pi/2? | |
Ans. The limit of sec(x) as x approaches pi/2 does not exist. The secant function becomes unbounded as x approaches pi/2, oscillating between negative and positive infinity.
Related Exams
About this Document
|
1.6K Views |
|
4.73/5 Rating |
|
Dec 22, 2024 Last updated |
Document Description: Limits of Trigonometric Functions for Commerce 2024 is part of Mathematics (Maths) Class 11 preparation.
The notes and questions for Limits of Trigonometric Functions have been prepared according to the Commerce exam syllabus. Information about Limits of Trigonometric Functions covers topics
like and Limits of Trigonometric Functions Example, for Commerce 2024 Exam. Find important definitions, questions, notes, meanings, examples, exercises and tests below for Limits of Trigonometric Functions.
Introduction of Limits of Trigonometric Functions in English is available as part of our Mathematics (Maths) Class 11
for Commerce & Limits of Trigonometric Functions in Hindi for Mathematics (Maths) Class 11 course.
Download more important topics related with notes, lectures and mock test series for Commerce
Exam by signing up for free. Commerce: Limits of Trigonometric Functions | Mathematics (Maths) Class 11 - Commerce
Description
Full syllabus notes, lecture & questions for Limits of Trigonometric Functions | Mathematics (Maths) Class 11 - Commerce - Commerce | Plus excerises question with solution to help you revise complete syllabus for Mathematics (Maths) Class 11 | Best notes, free PDF download
Information about Limits of Trigonometric Functions
In this doc you can find the meaning of Limits of Trigonometric Functions defined & explained in the simplest way possible. Besides explaining types of
Limits of Trigonometric Functions theory, EduRev gives you an ample number of questions to practice Limits of Trigonometric Functions tests, examples and also practice Commerce
tests
|
Explore Courses for Commerce exam
|
|
Signup for Free!
Signup to see your scores go up within 7 days! Learn & Practice with 1000+ FREE Notes, Videos & Tests.
Related Searches
ppt
,Limits of Trigonometric Functions | Mathematics (Maths) Class 11 - Commerce
,Exam
,Semester Notes
,Sample Paper
,Viva Questions
,practice quizzes
,shortcuts and tricks
,Important questions
,Limits of Trigonometric Functions | Mathematics (Maths) Class 11 - Commerce
,Extra Questions
,Objective type Questions
,video lectures
,Previous Year Questions with Solutions
,past year papers
,Limits of Trigonometric Functions | Mathematics (Maths) Class 11 - Commerce
,Free
,study material
,mock tests for examination
,MCQs
,Summary
;
Additional Information about Limits of Trigonometric Functions for Commerce Preparation
Limits of Trigonometric Functions Free PDF Download
The Limits of Trigonometric Functions is an invaluable resource that delves deep into the core of the Commerce exam.
These study notes are curated by experts and cover all the essential topics and concepts, making your preparation more efficient and effective.
With the help of these notes, you can grasp complex subjects quickly, revise important points easily,
and reinforce your understanding of key concepts. The study notes are presented in a concise and easy-to-understand manner,
allowing you to optimize your learning process. Whether you're looking for best-recommended books, sample papers, study material,
or toppers' notes, this PDF has got you covered. Download the Limits of Trigonometric Functions now and kickstart your journey towards success in the Commerce exam.
Importance of Limits of Trigonometric Functions
The importance of Limits of Trigonometric Functions cannot be overstated, especially for Commerce aspirants.
This document holds the key to success in the Commerce exam.
It offers a detailed understanding of the concept, providing invaluable insights into the topic.
By knowing the concepts well in advance, students can plan their preparation effectively.
Utilize this indispensable guide for a well-rounded preparation and achieve your desired results.
Limits of Trigonometric Functions Notes
Limits of Trigonometric Functions Notes offer in-depth insights into the specific topic to help you master it with ease.
This comprehensive document covers all aspects related to Limits of Trigonometric Functions.
It includes detailed information about the exam syllabus, recommended books, and study materials for a well-rounded preparation.
Practice papers and question papers enable you to assess your progress effectively.
Additionally, the paper analysis provides valuable tips for tackling the exam strategically.
Access to Toppers' notes gives you an edge in understanding complex concepts.
Whether you're a beginner or aiming for advanced proficiency, Limits of Trigonometric Functions Notes on EduRev are your ultimate resource for success.
Limits of Trigonometric Functions Commerce Questions
The "Limits of Trigonometric Functions Commerce Questions" guide is a valuable resource for all aspiring students preparing for the
Commerce exam. It focuses on providing a wide range of practice questions to help students gauge
their understanding of the exam topics. These questions cover the entire syllabus, ensuring comprehensive preparation.
The guide includes previous years' question papers for students to familiarize themselves with the exam's format and difficulty level.
Additionally, it offers subject-specific question banks, allowing students to focus on weak areas and improve their performance.
Study Limits of Trigonometric Functions on the App
Students of Commerce can study Limits of Trigonometric Functions alongwith tests & analysis from the EduRev app,
which will help them while preparing for their exam. Apart from the Limits of Trigonometric Functions,
students can also utilize the EduRev App for other study materials such as previous year question papers, syllabus, important questions, etc.
The EduRev App will make your learning easier as you can access it from anywhere you want.
The content of Limits of Trigonometric Functions is prepared as per the latest Commerce syllabus.
|
© EduRev
|
Education Revolution
|
|
Signup to see your scores
go up within 7 days!
Access 1000+ FREE Docs, Videos and Tests
Takes less than 10 seconds to signup