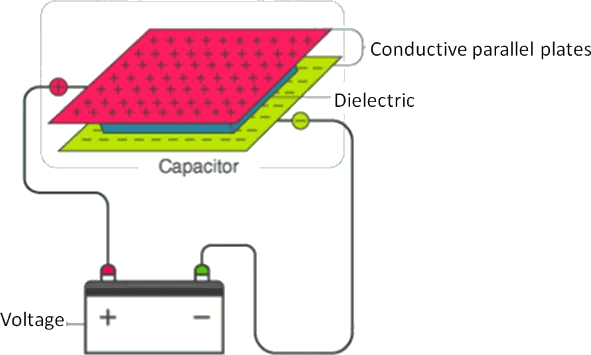
Energy Stored in a Capacitor | Physics for JEE Main & Advanced PDF Download
Energy Stored in a Charged capacitor
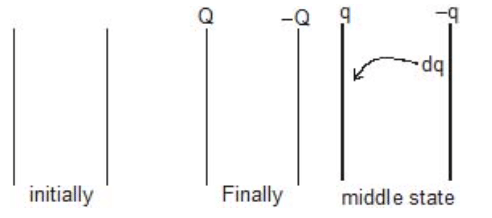
Work has to be done in charging a conductor against the force of repulsion by the already existing charges on it. The work is stored as a potential energy in the electric field of the conductor. Suppose a conductor of capacity C is charged to a potential V0 and let q0 be the charge on the conductor at this instant. The potential of the conductor when (during charging) the charge on it was q (< q0) is,
Now, work done in bringing a small charge dq at this potential is,
Therefore, total work done in charging it from 0 to q0 is,
This work is stored as the potential energy,
Therefore,
Further by using q0 = CV0 we can write this expression also as,
In general if a conductor of capacity C is charged to a potential V by giving it a charge q, then
3.1 Energy Density of a Charged Capacitor
This energy is localized on the charges or the plates but is distributed in the field. Since in case of a parallel plate capacitor, the electric field is only between the plates, i.e., in a volume (A × d), the energy density
or
3.2 Calculation of Capacitance
The method for the calculation of capacitance involves integration of the electric field between two conductors or the plates which are just equipotential surfaces to obtain the potential difference Vab. Thus,
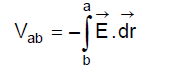
Therefore,
3.3 Heat Generated :
(1) Work done by battery
W = QV
Q = charge flow in the battery
V = EMF of battery
(2) W = Ve (When Battery discharging)
W = -Ve (When Battery charging)
(3) Q = CV (C = equivalent capacitance)
so W = CV × V = CV2
Now energy on the capacitor
Therefore, Energy dissipated in form of heat (due to resistance)
H = Work done by battery - {final energy of capacitor - initial energy of capacitor}
Ex.3 At any time S1 switch is opened and S2 is closed then find out heat generated in circuit.
Sol.
Charge flow through battery = Qf - Qi
= 2CV - CV = CV
H = (CV × 2V) -
Ex.4 (a) Find the final charge on each capacitor if they are connected as shown in the figure.
Sol. Initially
Finally let q charge flows clockwise then
Now applying KVL
5q + 50 + 5q - 200 + 2q = 0
12 q - 150 = 0 ⇒
so finally
(b) Find heat loss in the above circuit.
ΔH = Energy [initially - finally] on capacitor
Distribution of Charges on Connecting two Charged Capacitors :
When two capacitors C1 and C2 are connected as shown in figure
Before connecting the capacitors | ||
Parameter | Ist Capacitor | IInd Capacitor |
Capacitance | C1 | C2 |
Charge | Q1 | Q2 |
Potential | V1 | V2 |
After connecting the capacitors | ||
Parameter | Ist Capacitor | IInd Capacitor |
Capacitance | C1 | C2 |
Charge | ||
Potential | V1 | V2 |
(a) Common potential :
By charge conservation on plates A and C before and after connection.
Q1 + Q2 = C1V + C2V
⇒ =
(b)
(c) Heat loss during redistribution :
The loss of energy is in the form of Joule heating in the wire.
- When plates of similar charges are connected with each other ( with and - with -) then put all values (Q1, Q2, V1, V2) with positive sign.
- When plates of opposite polarity are connected with each other ( with -) then take charge and potential of one of the plate to be negative.
Derivation of above formulae :
Let potential of B and D is zero and common potential on capacitors is V, then at A and C it will be V.
C1V + C2V = C1V1 + C2V2
=
H =
when oppositely charged terminals are connected then
Therefore, C1V C2V = C1V1 - C2V2
Ex.5 Find out the following if A is connected with C and B is connected with D.
(i) How much charge flows in the circuit.
(ii) How much heat is produced in the circuit.
Sol. Let potential of B and D is zero and common potential on capacitors is V, then at A and C it will be V.
By charge conservation,
3V + 2V = 40 + 30
5V = 70 ⇒ V = 14 volt
Charge flow = 40 - 28 = 12 μC
Now final charges on each plate is shown in the figure.
(ii) Heat produced = × 2 × (20)2
× 3 × (10)2 -
× 5 × (14)2
= 400 150 - 490
= 550- 490 = 60 mJ
- When capacitor plates are joined then the charge remains conserved.
- We can also use direct formula of redistribution as given above.
Ex.6 Repeat above question if A is connected with D and B is connected with C.
Sol. Let potential of B and C is zero and common potential
on capacitors is V, then at A and D it will be V
2V + 3V = 10 ⇒ V = 2 volt
Now charge on each plate is shown in the figure.
Heat produced = 400 + 150 - 1
Therefore 2 × 5 × 4
= 550 - 10 = 540 μJ
- Here heat produced is more. Think why ?
Ex.7 Three capacitors as shown of capacitance 1mF, 2mF and 2mF are charged upto potential difference 30 V, 10 V and 15V respectively. If terminal A is connected with D, C is connected with E and F is connected with B. Then find out charge flow in the circuit and find the final charges on capacitors.
Sol. Let charge flow is q.
Now applying Kirchhoff's voltage low
- 2q = - 25
q = 12.5 mC
Final charges on plates
|
268 videos|740 docs|171 tests
|
FAQs on Energy Stored in a Capacitor - Physics for JEE Main & Advanced
| 1. What is the formula to calculate the energy stored in a capacitor? |  |
| 2. How does the capacitance affect the energy stored in a capacitor? |  |
| 3. Does the voltage across the capacitor impact the energy stored? |  |
| 4. Can the energy stored in a capacitor be negative? |  |
| 5. How can the energy stored in a capacitor be discharged? |  |