Combination of Capacitors | Physics for JAMB PDF Download
How Capacitors are connected?
Capacitors combination can be made in many ways. The combination is connected to a battery to apply a potential difference (V) and charge the plates (Q). We can define the equivalent capacitance of the combination between two points to be: C = Q/V
Two frequently used methods of combination are:
- Parallel combination
- Series combination
Parallel Combination of Capacitors
When one plate of one capacitor is connected with one plate of the other capacitor, such combination is called parallel combination.
All capacitors have the same potential difference but different charges.
We can say that : Q1 = C1V
Q1 = Charge on capacitor C1
C1 = Capacitance of capacitor C1
V = Potential across capacitor C1
The charge on the capacitor is proportional to its capacitance Q µ C
Where Q = Q1 + Q2 + Q3 ..............
Key Points:
- The maximum charge will flow through the capacitor of the largest value.
- Equivalent capacitance of parallel combination, Ceq = C1 + C2 + C3
- Equivalent capacitance is always greater than the largest capacitor of combination.
- Half of the energy supplied by the battery is stored in the form of electrostatic energy and half of the energy is converted into heat through resistance.
- Energy stored in the combination :
Formulae Derivation for Parallel combination:
A parallel combination of three capacitors, with one plate of each capacitor connected to one side of the circuit and the other plate connected to the other side, is illustrated in Figure.
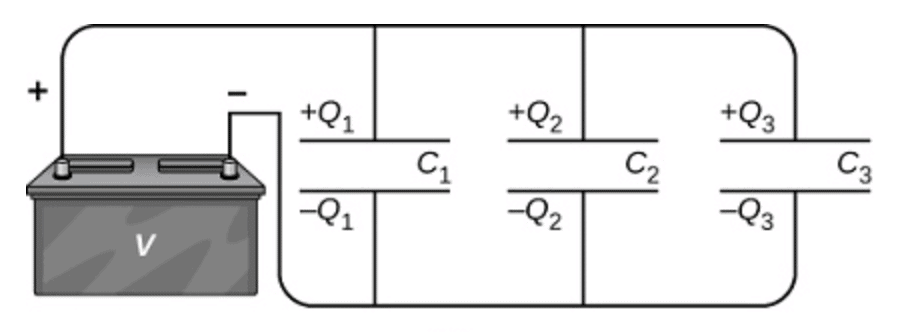
Since the capacitors are connected in parallel, they all have the same voltage V across their plates. However, each capacitor in the parallel network may store a different charge. To find the equivalent capacitance 𝐶𝑝 of the parallel network, we note that the total charge Q stored by the network is the sum of all the individual charges:
𝑄 = 𝑄1 + 𝑄2 + 𝑄3
On the left-hand side of this equation, we use the relation 𝑄 = 𝐶𝑝𝑉, which holds for the entire network. On the right-hand side of the equation, we use the relations
𝑄1 = 𝐶1𝑉 , 𝑄2 = 𝐶2𝑉 , and 𝑄3 = 𝐶3𝑉 for the three capacitors in the network.
In this way we obtain 𝐶𝑝𝑉 = 𝐶1𝑉 + 𝐶2𝑉 + 𝐶3𝑉.
This equation, when simplified, is the expression for the equivalent capacitance of the parallel network of three capacitors: 𝐶𝑝 = 𝐶1 + 𝐶2 + 𝐶3
This expression is easily generalized to any number of capacitors connected in parallel in the network.
Series Combination of Capacitors
When initially uncharged capacitors are connected as shown, then the combination is called series combination
All capacitors will have the same charge but different potential difference across them.
We can say that
V1 = potential across C1
Q = charge on positive plate of C1
C1 = capacitance of capacitor similarly
V1 : V2 : V3 =
We can say that potential difference across capacitor is inversely proportional to its capacitance in series combination.
Key Points:
- In a series combination, the smallest capacitor gets maximum potential.
-
,
,
Where V = V1 + V2 + V3 - Equivalent Capacitance:
Equivalent capacitance of any combination is that capacitance which when connected in place of the combination stores the same charge and energy as that of the combination
In series:........................
- In series, the combination equivalent is always less than the smallest capacitor of the combination.
- Half of the energy supplied by the battery is stored in form of electrostatic energy and half of the energy is converted into heat through resistance.
- Energy stored in the combination:
Ucombination =
Ucombination =
The energy supplied by the battery in charging the combination
Ubattery = Q × V = Q .=
Formulae Derivation for Series combination:
Let the capacitance of each capacitor be C1, C2 and C3 and their equivalent capacitance is Ceq.
As these capacitors are connected in series, thus charge across each capacitor is same as Q. When some electrical components, let say 3, are connected in series with each other, the potential difference of the battery V gets divided across each component as
V1, V2 and V3 as shown in the figure.
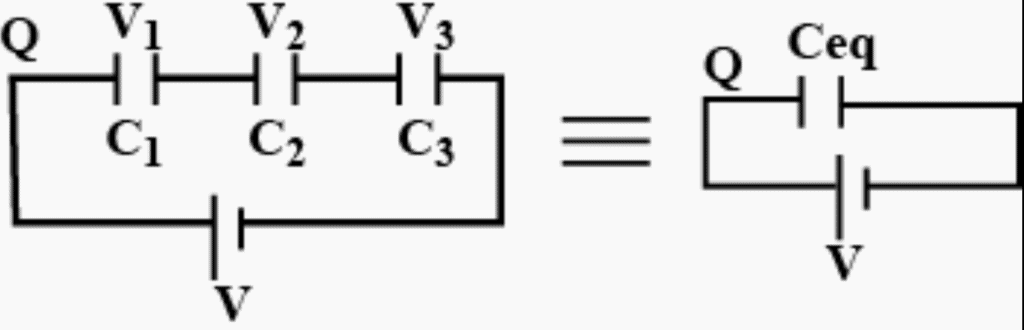
∴ V = V1 + V2 + V3
Using V = Q/C

Equivalent capacitance for series combination = 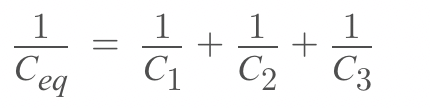
In general, 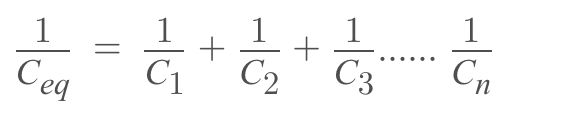
Solved Examples:
Example 1: Find charge on each capacitor.
Sol. Charge on C1 = C1V1 = 2 × (20 - 5)μC
= 30 μC
Charge on C2 = C2V2 = 2 × (20 - (-10))μC
= 60 μC
Charge on C3 = C3V3 = 4 × (20 - 10)μC
= 40 μC
Example 2: Find charge on each capacitor.
Sol. Charge on C1 = (x - 10) C1
Charge on C2 = (x - 0) C2
Charge on C3 = (x - 20) C3
Now from charge conservation at node x
(x - 10)C1 (x - 0)C2 (x - 20)C3 = 0
⇒ 2x - 20 2x 4x - 80 = 0
⇒ x = 25 Therefore
so
Example 3: In the given circuit find out the charge on each capacitor. (Initially they are uncharged)
Sol. Let potential at A is 0, so at D it is 30 V, at F it is 10 V and at point G potential is -25V. Now apply Kirchhoff's Ist law at point E. (total charge of all the plates connected to 'E' must be same as before i.e. 0)
Therefore, (x - 10) + (x - 30) 2 +(x 25) 2 = 0
5x = 20
x = 4
Final charges :
Q2mF = (30 - 4) 2 = 52 mC
Q1mF = (10 - 4) = 6 mC
Q2mF = (4 - (-25)) 2 = 58 mC
Example 4:
Find voltage across capacitor C1.
Sol.
Now from charge conservation at node x and y
for x
(x - 4)C1 + (x - 2)C2 + (x - y)C3 = 0 ⇒
2(x - 4) + 2(x - 2) (x - y) 2 = 0
6x - 2y - 12 = 0 .....(1)
For y
(y - x)C3 + [y -(-4)]C4 (y - 0)C5 = 0 ⇒ (y - x)2 (y 4) 2 y 2 = 0
= 6y - 2x 8 = 0 .....(2)
eq. (1) & (2)
y = - 3 Therefore
x = 7 Therefore
So potential difference = x - y =
Example 5: Three initially uncharged capacitors are connected in series as shown in circuit with a battery of emf 30V. Find out following :
(i) charge flow through the battery,
(ii) potential energy in 3 mF capacitor. 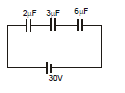
(iii) Utotal in capacitors
(iv) heat produced in the circuit
Sol.
Ceq = 1 μF.
(i) Q = Ceq V = 30 μC
(ii) charge on 3μF capacitor = 30 μC
energy = =
= 150 μJ
(iii) Utotal = = 450 μJ
(iv) Heat produced = (30 μC) (30) - 450 μJ = 450 μJ
Example 6: Two capacitors of capacitance 1 mF and 2mF are charged to potential difference 20 V and 15 V as shown in figure. If now terminal B and C are connected together terminal A with positive of battery and D with negative terminal of battery then find out final charges on both the capacitor.
Now applying kirchhoff voltage law
- 40 - 2q - 30 - q = - 60
3q = - 10
Charge flow = - μC.
Charge on capacitor of capacitance 1μF = 20 q =
Charge on capacitor of capacitance 2μF = 30 q =
|
260 videos|253 docs|230 tests
|
FAQs on Combination of Capacitors - Physics for JAMB
| 1. How are capacitors connected in parallel? |  |
| 2. What is the formula for calculating the total capacitance in a parallel combination of capacitors? |  |
| 3. How are capacitors connected in series? |  |
| 4. What is the formula for calculating the total capacitance in a series combination of capacitors? |  |
| 5. Can capacitors be combined in both parallel and series combinations in the same circuit? |  |

















