Some Results on Binomial Coefficients and Negative or Fractional Indices | Mathematics (Maths) Class 11 - Commerce PDF Download
In this explainer, we will learn how to use the binomial expansion to expand binomials with negative and fractional exponents.
Recall that the binomial theorem tells us that for any expression of the form ( 𝑎 + 𝑏 𝑥 ) 𝑛 where 𝑛 is a natural number, we have the expansion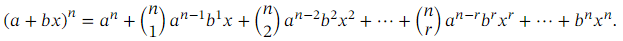
In particular, we can take 𝑎 = 𝑏 = 1 .
Theorem: Generalized Binomial Theorem, 𝑎 = 𝑏 = 1 Case
The expansion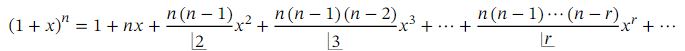
is valid when 𝑛 is negative or a fraction (or even an irrational number). In this case, the binomial expansion of ( 1 + 𝑥 ) 𝑛 (where 𝑛 is not a positive whole number) does not terminate; it is an infinite sum. Furthermore, the expansion is only valid for | 𝑥 | < 1.
Since the expansion of ( 1 + 𝑥 ) 𝑛 where 𝑛 is not a positive whole number is an infinite sum, we can take the first few terms of the expansion to get an approximation for ( 1 + 𝑥 ) 𝑛 when | 𝑥 | < 1 . Let us look at an example where we calculate the first few terms.
Example 1: Finding Terms of a Binomial Expansion with a Negative Exponent
Write down the first four terms of the binomial expansion of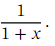
Answer Recall that the generalized binomial theorem tells us that for any expression of the form ( 1 + 𝑥 ) 𝑛 where 𝑛 is a real number, we have the expansion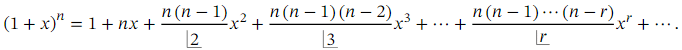
When 𝑛 is not a positive integer, this is an infinite series, valid when | 𝑥 | < 1
Note that we can rewrite 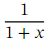 as ( 1 + 𝑥 ) -1 .This is an expression of the form ( 1 + 𝑥 ) 𝑛 ,with 𝑛 = − 1 .Therefore, the generalized binomial theorem tells us that
as ( 1 + 𝑥 ) -1 .This is an expression of the form ( 1 + 𝑥 ) 𝑛 ,with 𝑛 = − 1 .Therefore, the generalized binomial theorem tells us that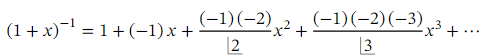 =1−𝑥+𝑥2−𝑥3+⋯,
=1−𝑥+𝑥2−𝑥3+⋯,
which is an infinite series, valid when | 𝑥 | < 1 .The first four terms of the expansion are 1 − 𝑥 + 𝑥2 − 𝑥3.
We can also use the binomial theorem to expand expressions of the form ( 1 + 𝑏 𝑥 ) 𝑛 for a constant 𝑏 .
Theorem: Generalized Binomial Theorem, 𝑎 = 1 Case
The expansion
(1+𝑏𝑥)n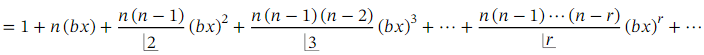
is an infinite series when 𝑛 is not a positive integer. It is valid when
Example 2: Finding a Missing Value in a Binomial Expansion and Finding the Coefficient of a Term in the Expansion
In the binomial expansion of ( 1 + 𝑏 𝑥 ) -5 ,the coefficient of 𝑥 is − 1 5 .Find the value of the constant 𝑏 and the coefficient of x2 .
Ans: Recall that the generalized binomial theorem tells us that for any expression of the form ( 1 + 𝑏 𝑥 ) 𝑛 where 𝑛 is a real number, we have the expansion
(1+𝑏𝑥)n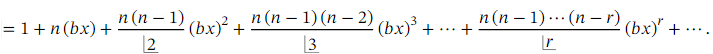
When 𝑛 is not a positive integer, this is an infinite series, valid when | 𝑏 𝑥 | < 1 or | 𝑥 | <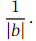
We begin by writing out the binomial expansion of ( 1 + 𝑏 𝑥 ) -5 up to and including the term in x2 :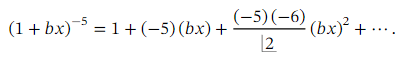
We are told that the coefficient of 𝑥 here is equal to − 1 5 ;that is,
− 5 𝑏 = − 1 5
𝑏 = 3 . To find the coefficient of x2 ,we can substitute the value of 𝑏 back into the expansion to get
To find the coefficient of x2 ,we can substitute the value of 𝑏 back into the expansion to get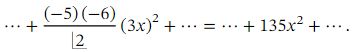
Therefore, the coefficient of x2 is 135 and the value of the constant 𝑏 is 3.
More generally still, we may encounter expressions of the form ( 𝑎 + 𝑏 𝑥 ) 𝑛 .Such expressions can be expanded using the binomial theorem. However, the theorem requires that the constant term inside the parentheses (in this case, 𝑎 ) is equal to 1. So, before applying the binomial theorem, we need to take a factor of 𝑎 𝑛 out of the expression as shown below: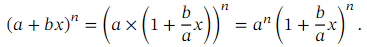
We now have the generalized binomial theorem in full generality.
Theorem: Generalized Binomial Theorem
The expansion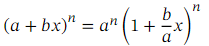
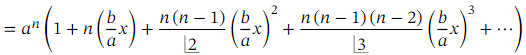
where 𝑛 is not a positive integer is an infinite series, valid when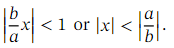
Let us look at an example of this in practice.
Example 3: Finding Terms of a Binomial Expansion with a Negative Exponent and Stating the Range of Valid Values
Write down the first four terms of the binomial expansion of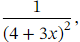 stating the range of values of 𝑥 for which the expansion is valid.
stating the range of values of 𝑥 for which the expansion is valid.
Ans: Recall that the generalized binomial theorem tells us that for any expression of the form ( 𝑎 + 𝑏 𝑥 ) 𝑛 where 𝑛 is a real number, we have the expansion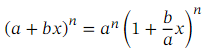
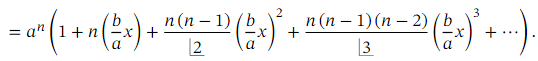
When 𝑛 is not a positive integer, this is an infinite series, valid when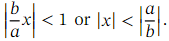
Applying this to 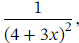 we have
we have 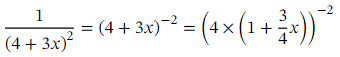
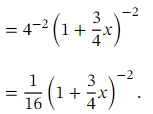
We can now expand the contents of the parentheses: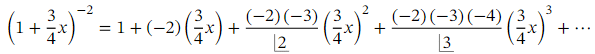
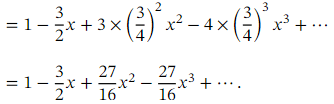
Therefore, the first four terms of the binomial expansion of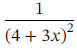 are
are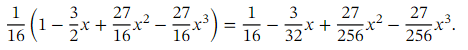
The expansion is valid for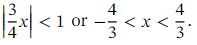
A classic application of the binomial theorem is the approximation of roots. Suppose we want to find an approximation of some root √ 𝑝 .The idea is to write down an expression of the form ( 𝑐 + 𝑑 𝑥 ) that we can approximate for some small 𝑥 (generally, smaller values of 𝑥 lead to better approximations) using the binomial expansion. The value of 𝑥 should be of the form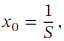 ,where 𝑆 is a perfect square and √ 𝑆 = 𝑠 ( 𝑆 = 1 0 0 or 𝑆 = 4 0 0 are often good choices). Then, we have
,where 𝑆 is a perfect square and √ 𝑆 = 𝑠 ( 𝑆 = 1 0 0 or 𝑆 = 4 0 0 are often good choices). Then, we have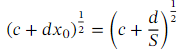
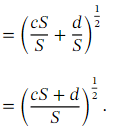
The trick is to choose 𝑐 and 𝑑 so that 𝑐 𝑆 + 𝑑 = 𝑅 𝑝 where 𝑅 is a perfect square, so √ 𝑅 = 𝑟 for some positive integer 𝑟 .Then, we have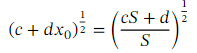
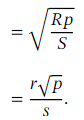
If our approximation using the binomial expansion gives us the value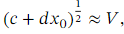 ,then we can recover an approximation for √ 𝑝 as follows:
,then we can recover an approximation for √ 𝑝 as follows: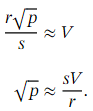
Let us see how this works in a concrete example.
Example 4: Finding an Approximation Using a Binomial Expansion
By finding the first four terms in the binomial expansion of 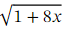 and then substituting in 𝑥 = 0 . 0 1 ,find a decimal approximation for √3 .
and then substituting in 𝑥 = 0 . 0 1 ,find a decimal approximation for √3 .
Ans: The goal here is to find an approximation for √ 3 .Note that the numbers 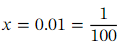 together with the 1 and 8 in √ 1 + 8 𝑥 have been carefully chosen. Indeed, substituting in the given value of 𝑥 ,we get
together with the 1 and 8 in √ 1 + 8 𝑥 have been carefully chosen. Indeed, substituting in the given value of 𝑥 ,we get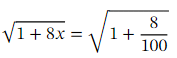
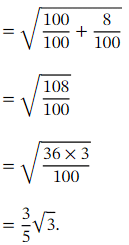
Thus, if we use the binomial theorem to calculate an approximation 𝑉 to at the value 𝑥 = 0 . 0 1 ,then we will get an approximation to √ 3 because
at the value 𝑥 = 0 . 0 1 ,then we will get an approximation to √ 3 because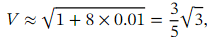
which implies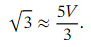
So, let us write down the first four terms in the binomial expansion of 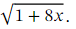
Recall that the generalized binomial theorem tells us that for any expression of the form ( 1 + 𝑏 𝑥 ) 𝑛 where 𝑛 is a real number, we have the expansion
(1+𝑏𝑥) 𝑛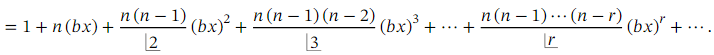
When 𝑛 is not a positive integer, this is an infinite series, valid when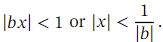
In this example, we have
=1+4𝑥−8𝑥+32𝑥+⋯.
We can now evaluate the sum of these first four terms at 𝑥 = 0 . 0 1 :
𝑉=1+4×0.01−8×(0.01 )+32 × (0.01 ) = 1+0.04−0.0008+0.000032=1.039232.
Therefore, we have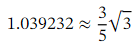

Comparing this approximation with the value appearing on the calculator for √3=1.732050807 … ,we see that this is accurate to 5 decimal places.
When making an approximation like the one in the previous example, we can calculate the percentage error between our approximation and the true value. The absolute error is simply the absolute value of difference of the two quantities: |−| true value approximation .To find the percentage error, we divide this quantity by the true value, and multiply by 100. We can calculate the percentage error in our previous example:
We can calculate the percentage error in our previous example: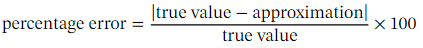

We can also use the binomial theorem to approximate roots of decimals, particularly in cases when the decimal in question differs from a whole number by a small value 𝑥 ,as in the next example.
Example 5: Using a Binomial Expansion to Approximate a Value
Write down the binomial expansion of 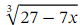 in ascending powers of 𝑥 up to and including the term in x2 and use it to find an approximation for
in ascending powers of 𝑥 up to and including the term in x2 and use it to find an approximation for 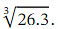 .Give your answer to 3 decimal places.
.Give your answer to 3 decimal places.
Ans: We want to approximate 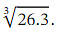 We notice that 26.3 differs from 27 by 0.7 = 7×0.1 .Therefore, if we evaluate
We notice that 26.3 differs from 27 by 0.7 = 7×0.1 .Therefore, if we evaluate 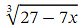 at 𝑥 = 0 . 1 ,then we will get
at 𝑥 = 0 . 1 ,then we will get 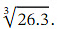 .We are going to use the binomial theorem to approximate
.We are going to use the binomial theorem to approximate 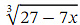 .Recall that the generalized binomial theorem tells us that for any expression of the form ( 𝑎 + 𝑏 𝑥 ) 𝑛 where 𝑛 is a real number, we have the expansion
.Recall that the generalized binomial theorem tells us that for any expression of the form ( 𝑎 + 𝑏 𝑥 ) 𝑛 where 𝑛 is a real number, we have the expansion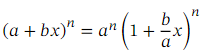
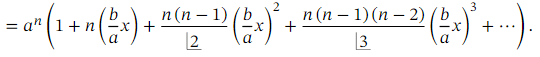
When 𝑛 is not a positive integer, this is an infinite series, valid when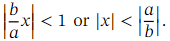
Let us write down the first three terms of the binomial expansion of 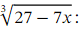
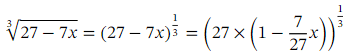
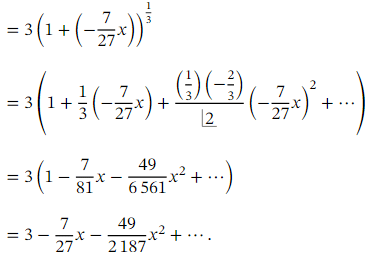
Evaluating the sum of these three terms at 𝑥 = 0 . 1 will give us an approximation for  as follows:
as follows: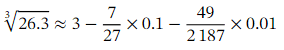
and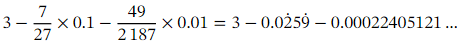
=2.97385002286….
Comparing this approximation with the value appearing on the calculator for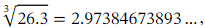 we see that it is accurate to four decimal places. Rounding to 3 decimal places, we have
we see that it is accurate to four decimal places. Rounding to 3 decimal places, we have 
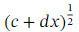
|
80 videos|315 docs|99 tests
|
FAQs on Some Results on Binomial Coefficients and Negative or Fractional Indices - Mathematics (Maths) Class 11 - Commerce
| 1. What are binomial coefficients? |  |
| 2. Are binomial coefficients only defined for positive integer indices? |  |
| 3. How can binomial coefficients be calculated for negative or fractional indices? |  |
| 4. What are some properties of binomial coefficients with negative or fractional indices? |  |
| 5. Can binomial coefficients with negative or fractional indices be interpreted geometrically? |  |
















