Binomial Theorem and Important Terms of Binomial Expansion | Mathematics (Maths) Class 11 - Commerce PDF Download
Binomial Theorem
A. Binomial Theorem
The formula by which any positive integral power of a binomial expression can be expanded in the form of a series is known as Binomial Theorem. If 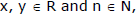 then
then
(x + y)n = nC0xn + nC1xn – 1y + nC2xn – 2 y2 + ........+ nCrxn–ryr + ......+ nCnyn 
This theorem can be proved by induction.
Observations :
(a) The number of terms in the expansion is (n + 1) i.e. one more than the index.
(b) The sum of the indices of x & y in each term is n.
(c) The binomial coefficients of the terms (nC0, nC1.........) equidistant from the beginning and the end are equal.
Ex.1 The value of 
Sol. The numerator is of the form a3 + b3 + 3ab (a + b) = (a + b)3 where a = 18, and b = 7
 Nr = (18 + 7)3 = (25)3. Denominator can be written as
Nr = (18 + 7)3 = (25)3. Denominator can be written as

= (3 + 2)6 = 56 = (25)3

B. IMPORTANT TERMS IN THE BINOMIAL EXPANSION ARE
(a) General term : The general term or the (r + 1)th term in the expansion of (x + y)n is given by
Tr+1 = nCrxn-r. yr
Ex.2 Find : (a) The coefficient of x7 in the expansion of 
(b) The coefficient of x-7 in the expansion of 
Also, find the relation between a and b, so that these coefficients are equal.
Sol.
(a) In the expansion of 
the general terms is 
putting 22 – 3r = 7 ⇒ 3r = 15 ⇒ r = 5

Hence the coefficient of 
(b) In the expansion of  ,
,
general terms is 
putting 11 – 3r = – 7 ⇒ 3r = 18 ⇒ r = 6

Hence the coefficient of 
Also given coefficient of 
= coefficient of 

⇒ ab = 1 ( ∴ 11C5 = 11C6). Which is a required relation between a and b.
Hence the coefficient of x–7 in 
Also given coefficient of x7 in 
11C5 a6 b-5 = 11C6 a5b-6 ⇒ ab = 1 (∵11C5 = 11C6). Which is a required relation between a and b.
Ex.3 Find the number of rational terms in the expansion of (91/4 + 81/6)1000.
Sol.
The general term in the expansion of (91/4 + 81/6)1000 is Tr + 1 = 
The above term will be rational if exponent of 3 and 2 are integers. i.e 1000-r/2 and r/2 must be integers
The possible set of values of r is {0, 2, 4, ..........1000}. Hence, number of rational terms is 501
(b) Middle term : The middle term(s) in the expansion of (x + y)n is (are)
(i) If n is even, there is only one middle term which is given by T(n + 2)/2 = nCn/2. xn/2. yn/2
(ii) If n is odd, there are two middle terms which are  &
& 
Ex.4 Find the middle term in the expansion of 
Sol.
The number of terms in the expansion of  is 10 (even). So there are two middle terms.
is 10 (even). So there are two middle terms.
 two middle terms. They are given by T5 and T6
two middle terms. They are given by T5 and T6




(c) TERM INDEPENDENT OF x : Term independent of x contains no x ; Hence find the value of r for which the exponent of x is zero.
Ex.5 The term independent of x in 
Sol. General term in the expansion is 
For constant term, 3r/2 = 10, r = 20/3 which is not an integer. Therefore, there will be no constant term.
(d) NUMERICALLY GREATEST TERM : To find the greatest term in the expansion of (x + a)n.
We have  therefore, since xn multiplies every term in
therefore, since xn multiplies every term in  , it will be sufficient to find the greatest term in this later expansion. Let the Tr and Tr + 1 be the rth and (r +1)th terms in the expansion of
, it will be sufficient to find the greatest term in this later expansion. Let the Tr and Tr + 1 be the rth and (r +1)th terms in the expansion of  Let numerically, Tr + 1 be the greatest term in the above expansion. Then
Let numerically, Tr + 1 be the greatest term in the above expansion. Then


Substituting values of n and x, we get r < m + f or r < m where m is a positive integer and f is fraction such that 0 < f < 1. In the first case Tm + 1 is the greatest term, while in the second case Tm and Tm + 1 are the greatest terms and both are equal.
Ex.6 Find numerically the greatest term in the expansion of (3 – 5x)11 when x = 1/5
Sol. Since 




so, the greatest terms are T2 + 1 and T3+1. Greatest term (when r = 2)


and greatest term (when r = 3) 

From above we say that the value of both greatest terms are equal.
C. If ( √A +B)n = I + f , where I & n are positive integers, n being odd and 0 < f < 1, then (I + f). f = Kn where A – B2 = K > 0 & A – B <1 . If n is an even integer, then (I + f) (1 – f) = kn
Ex.7 If (6√6 + 14)2n+1 = [N] + F and F = N – [N] ; where [*] denotes greatest integer, then NF is equal to
Sol. Since (6√6 + 14)2n+1 = [N] + F. Let us assume that f = (6√6 – 14)2n+1 ; where 0 ≤ f < 1.


[N] + F – f = even integer.
Now 0 < F < 1 and 0 < f < 1 so –1 < F – f < 1 and F – f is an integer so it can only be zero
Thus NF = (6√6 + 14)2n+1 (6√6 – 14)2n+1 = 202n + 1.
|
75 videos|238 docs|91 tests
|
FAQs on Binomial Theorem and Important Terms of Binomial Expansion - Mathematics (Maths) Class 11 - Commerce
| 1. What is the Binomial Theorem? |  |
| 2. What are the important terms used in binomial expansion? |  |
| 3. How can the Binomial Theorem be applied to expand binomial expressions? |  |
| 4. What is the significance of the Binomial Theorem in mathematics? |  |
| 5. Can the Binomial Theorem be used for negative exponents? |  |

|
Explore Courses for Commerce exam
|

|


















