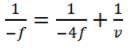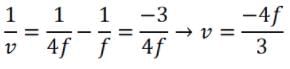Types of Mirrors, Mirror Formula and Applications | Physics Class 12 - NEET PDF Download
Just imagine living a day without mirrors. How will you get dressed to go to school? While driving, how will you be able to see vehicles behind and on the sides? How will you check out the look of new clothes when you go to shop in the market? It is practically impossible to live without mirrors. In this document, we will study mirrors and their types in detail.
What is a Mirror?
A mirror is a smooth and highly polished surface designed to reflect light in a way that preserves the physical characteristics of the original light. This can be attributed to the law of reflection.
 Law of Reflection
Law of Reflection
- Law of Reflection: The law of reflection dictates that when a beam of light is directed at a smooth, highly polished surface, the angle of reflection of the light is equal to its angle of incidence, and both rays are perpendicular to the surface at the point of contact.
- Made up of: Mirrors are commonly made of materials like glass, metal, or plastic, and have a wide range of uses, from personal grooming to scientific instruments.
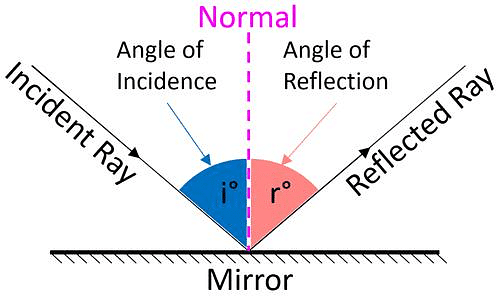
Different Types of Mirrors
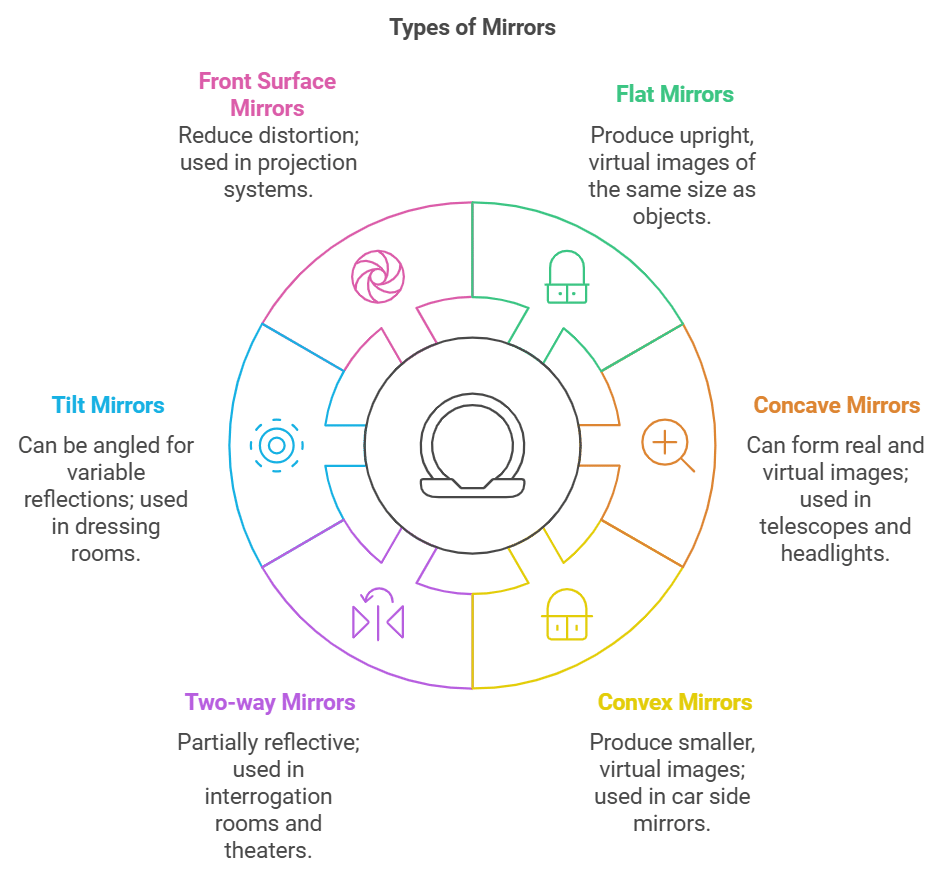
There are several types of mirrors, each with unique characteristics and uses. Some of the most common types of mirrors are:
 Types of mirrors
Types of mirrors
- Flat/Plane mirrors: Plane mirrors have a flat, smooth surface and produce an upright, virtual image that is the same size as the object being reflected.
- Concave mirrors: These mirrors have a surface that curves inward like inside of a spoon. They can form both real and virtual images, depending on the distance of the object from the mirror and the curvature of the mirror. Concave mirrors are used in telescopes, headlights, and makeup mirrors.
- Convex mirrors: These mirrors have a surface that curves outward, like the back of a spoon. They produce a virtual image that is smaller than the object being reflected, and the image appears farther away than it actually is. Convex mirrors are used in car side mirrors and security mirrors.
- Two-way mirrors: Also known as a one-way mirror, this type of mirror is partially reflective and partially transparent, allowing people on one side to see through the mirror while those on the other side see only a reflection. Two-way mirrors are used in interrogation rooms, movie theatres, and some types of windows.
- Tilt mirrors: These mirrors can be tilted to different angles, allowing for a variable reflection. They are often used in dressing rooms and makeup studios.
- Front surface mirrors: These mirrors have the reflective surface on the front, or first surface, of the mirror, rather than on the back. This reduces distortion and is useful in applications such as projection systems and optical instruments.
 Different Types of Mirrors
Different Types of Mirrors
Each type of mirror has unique properties that make it suitable for different applications, and understanding these properties is important for choosing the right mirror for a particular use.
Properties Related to Plane Mirror
A plane mirror is a flat and smooth reflecting surface that reflects light in a way that preserves the physical characteristics of the original light. The following are some important properties and terms related to a plane mirror:
Properties:
- Nature: The image formed by a plane mirror is virtual, which means it cannot be projected on a screen.
- Orientation: The image is always erect, which means it appears in the same orientation as the object being reflected.
- Lateral inversion: The image is laterally inverted, which means it appears flipped horizontally.

In the image formed by a plane mirror the right side of the object appears as the left side and vice-versa. This phenomenon is called lateral inversion.
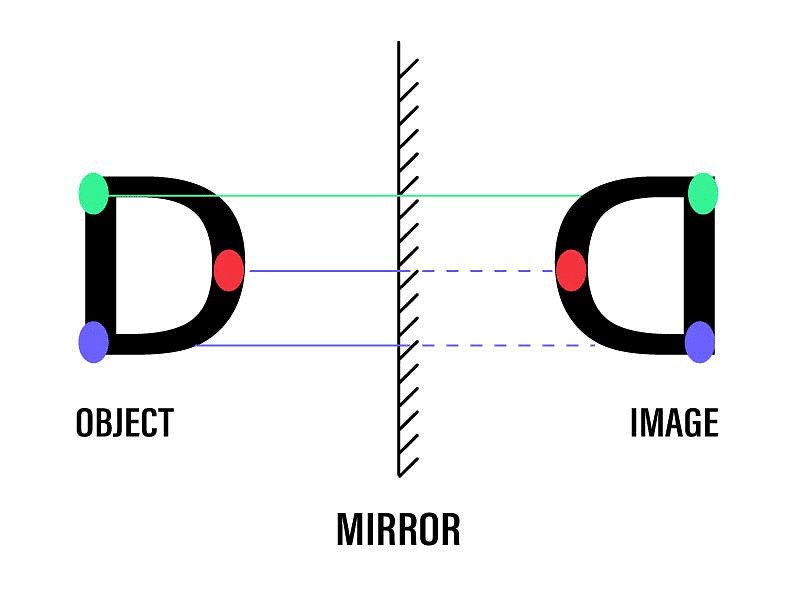 Image formed by a plane mirror
Image formed by a plane mirror
- Size: The size of the image is equal to the size of the object.
- Distance of image from object: The distance of the image from the mirror is equal to the distance of the object from the mirror.
- Magnification: The magnification of the image is unity, which means it is of the same size as the object.
 Image formed by a plane mirror
Image formed by a plane mirror
Calculations:
- A plane mirror may form a virtual as well as a real image. A man may see his full image in a mirror of the height of a man.
- When two plane mirrors are held at an angle θ, the number of images of an object placed between them is given below:
(a) n = [(360° / θ) – 1 ], where 360° / θ is an integer.
(b) n = integral part of 360° / θ, when 360° is not an integer. - A plane mirror may form a real image when the pencil of light incident on the mirror is convergent. Children, during their play, form an image of the sun as a wall by a strip of a plane mirror.
- Kaleidoscope and periscope employ the principle of image formation by a plane mirror. If keeping an object fixed a plane mirror is rotated in its plane by an angle θ, then the reflected ray rotates in the same direction by an angle 2 θ.
 Image formed by a Periscope
Image formed by a Periscope
- The focal length, as well as the radius of curvature of a plane mirror, is infinity. The power of a plane mirror is zero.
- An image formed by a plane mirror is virtual, erect, laterally inverted, of the same size as that of the object, and at the same distance as the object from the mirror.
Properties and Terms Related to Spherical Mirrors
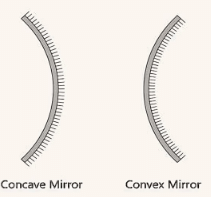
A highly polished curved surface whose reflecting surface is a cut part of a hollow at glass sphere is called a spherical mirror.
Spherical mirrors are of two types:
(i) Concave Mirror: A spherical mirror whose bent surface is reflecting surface, is called a concave mirror.
 Types of Spherical Mirrors
Types of Spherical Mirrors
(ii) Convex Mirror: A spherical mirror whose bulging out surface is reflecting surface, is called a convex mirror.
Some Terms Related to Spherical Mirrors are Given Below:
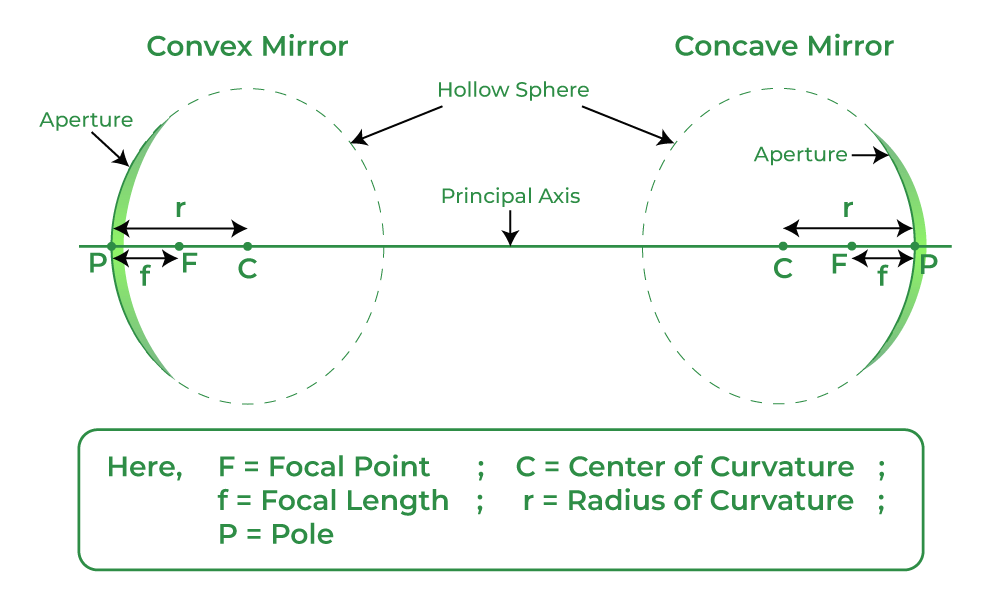
- Centre of Curvature: It is the center of the sphere of which the mirror or lens is a part.
- The radius of Curvature (r): The radius of the hollow sphere of which the mirror is a part, is called the radius of curvature.
- Pole: The central point of the spherical mirror is called its pole (P) or vertex.
- Aperture: The portion of a mirror from which the reflection of light actually takes place is called the aperture of the mirror. The aperture of a mirror represents the size of the mirror.
- Focus: When a parallel beam of light rays is incident on a spherical mirror, then after reflection it meets or appears to meet at a point on the principal axis, which is called the focus of the spherical mirror.
- Focal Length: The distance between the pole and the focus is called the focal length (f).
The relation between focal length and radius of curvature is given by:
f=r/2
The power of a mirror is given as P = 1/f (meter)
 Terms related to Spherical Mirrors
Terms related to Spherical Mirrors
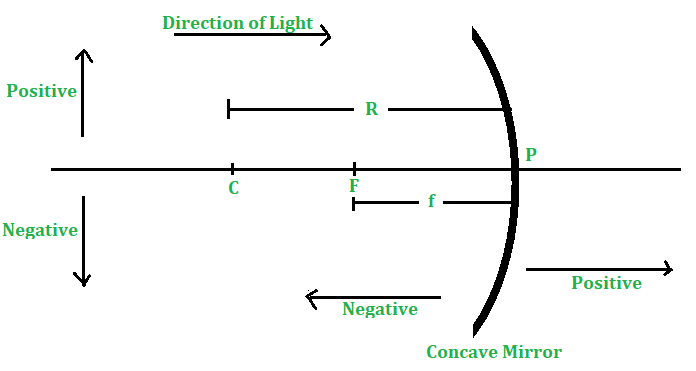
Sign Convention for Spherical Mirrors
- All distances are measured from the pole of the mirror.
- Distances measured in the direction of incident light rays are taken as positive.
- Distances measured in the opposite direction to the incident light rays are taken as negative.
- Distances measured above the principal axis are positive.
- Distances measured below the principal axis are negative.
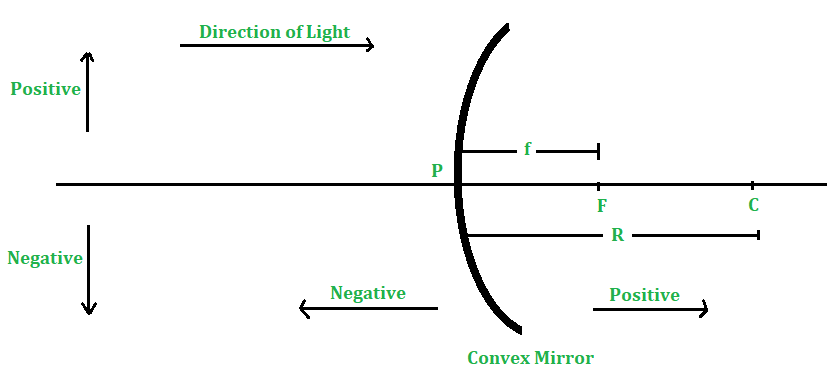 Sign Convention for Convex Mirror
Sign Convention for Convex Mirror
Mirror Formula for Concave Mirror
Let us consider a point object placed beyond C of a concave mirror. To obtain the image, we make the ray diagram; we can take any two rays.
1. The first ray goes straight along the principal axis and after reflection, it retraces the same path.
2. Another ray is taken, which makes an angle of 𝜃 to the normal drawn and reflects back towards the principal axis.
Both the rays, after reflection, meet each other at some point, say I, that is between F and C. The image is formed at point I.
Let us assume the angle subtended by the object, image, and the center of curvature with the principal axis be 𝛼, 𝛽, and 𝛾.
For triangle AOC,
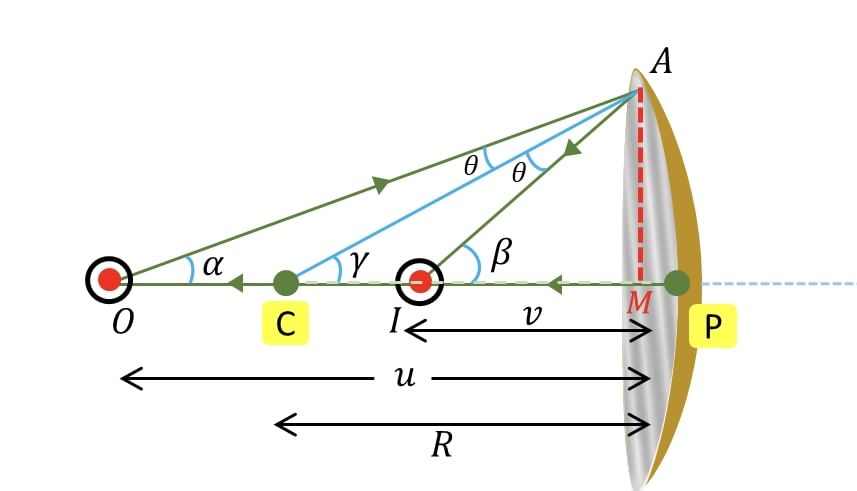 Concave Mirror
Concave Mirror

By subtracting equation (ii) from equation (i), we get the following:
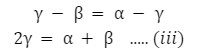
The perpendicular drawn from A meets the principal axis at M, and M is very close to P. So, we can treat them as the same points, i.e., AM ≈ AP.
From the diagram,
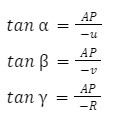
For small angle,
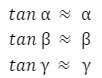
By substituting the above values in equation (iii), we get the following
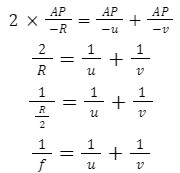
This is the mirror formula for a concave mirror.
Mirror Formula for Convex Mirror
Let us take a convex mirror of a small aperture and let the object be placed somewhere between P and infinity. To obtain the image, we make the ray diagram and we can take any two rays.
1. The first ray goes along the principal axis and is extended towards the back of the mirror.
2. The second ray falls on the mirror at an angle of 𝜃 with the normal at that point and gets reflected. On extending the reflected ray behind the mirror, it meets the principal axis at some point between P and F.
Both the rays after reflection meet each other at some point, say I, which is between P and F. The image is formed at point I.
Let us assume the angle subtended by the object, image, and the center of curvature with the principal axis be 𝛼, 𝛽, and 𝛾.
 Convex Mirror
Convex Mirror
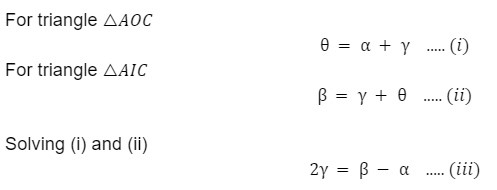
The perpendicular drawn from A meets the principal axis at a point very close to P.
So, from the diagram,
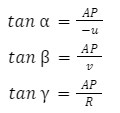
For small angle ,
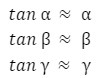
By substituting the above values in equation (iii), we get the following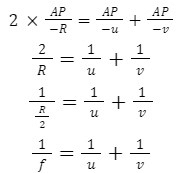
This is the mirror formula for a convex mirror which is the same as a concave mirror.
Mirror Formula: 1/f = 1/v + 1/u
where, f = focal length of the mirror, u = distance of the object, and v = distance of the image.
Newton’s formula for a concave mirror:
⇒
where x1 and x2 are the distances of the object and image from the focus.
Example 1: What is the image distance of a concave mirror if the object distance is 16 cm? It is given that the focal length of the mirror is 8 cm.
Solution:
As we know the mirror formula: 1/v + 1/u = 1/f
where, u = object distance = -16 cm
v = image distance = ?
f = focal length of the mirror = -8 cm
Putting the values we get,
1/v + 1/-16 = 1/-8
or, 1/v = -1/16
or, v = -16 cm
Therefore, the object is located 16 cm in the front mirror.
Example 2: Find the image distance of convex mirror if the object distance is 10 cm? It is given that the focal length of the mirror is 10 cm.
Solution:
As we know the mirror formula: 1/v + 1/u = 1/f
where, u = object distance = -10 cm
v = image distance = ?
f = focal length of the mirror = =10 cm
Putting the values we get,
1/v + 1/-10 = 1/10
or, 1/v = 1/10 – (1/-10)
or, 1/v = 1/10 + 1/10
or, 1/v = 2/10
or, 1/v = 1/5
or, v = 5 cm
Therefore, the image is located 5 cm behind the mirror.
What is Magnification?
Magnification is a measure of the extent to which an object's size is visually enlarged or reduced by an optical system, such as a lens or a mirror. It is the ratio of the size of the image produced by the optical system to the size of the object itself.
- Magnification can be expressed as a positive number for an image that is larger than the object or as a negative number for an image that is smaller than the object.
- The magnification of an optical system depends on the characteristics of the system, such as the focal length of the lens or mirror, the distance between the object and the optical system, and the distance between the image and the optical system. Here are the different types of magnification and the calculations associated with them:
1. Linear Magnification - The ratio of the height of the image (I) formed by a mirror to the height of the object (O) is called linear magnification (m).
Linear magnification (m) = I/O = -v/u
2. Areal and Axial Magnification -
- The ratio of the area of an image to the area of an object is called areal magnification.
- Areal magnification =
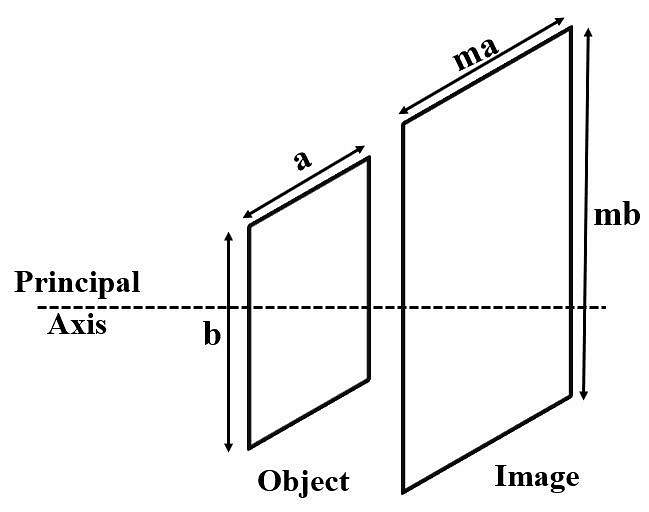 Areal Magnification
Areal Magnification
- When a small object is placed linearly along the principal axis, its longitudinal or axial magnification is given by
- Axial magnification
Example 1: What is the magnification if the object height is 12 cm and the image height is 48 cm below the principal axis?
Solution:
As we know the magnification can be calculated using the following formulas: m = h’/h
Given, height of the image h’ = -48 cm, height of the object (h) = +12 cm
The signs are given using sign convention.
therefore, m = h’/h
or, m = -48 cm/ 12 cm
0r, m = -4
Thus the magnification is -4.
Example 2: Rohit kept a pencil perpendicular to the principal axis of a concave mirror just ahead of it. The Mirror has a focal length of 30 cm. The image produced is two times the pencil size. If the image is real, what is the object's distance from the mirror?
Solution:
Magnification =h(i)/h(o) =−v/u
For real image
m=−v/u=−2
v=2u
Using the mirror equation,
1/v+1/u=1/f
1/2u+1/u=1/−30
u=-45 cms.
Applications of Spherical Mirrors
When the object lies too close to a concave mirror, it forms a virtual, upright, and magnified image of the object. This property of concave mirrors is used in
- Shaving mirrors
- Makeup mirrors
- Dental mirrors.
As all the above mirrors are required to produce a magnified image of the person in front of it, concave mirrors are used. A concave mirror can also direct the light from a source (spreading in all directions) in one direction by reflecting it. Because of this property, concave mirrors are used in
- Headlights of vehicles
- Torches

A convex mirror covers a wide area in the image it forms. Because of this property, it is used as:
- Rear-view mirror in the vehicles to see the vehicles approaching from behind.
- Shop security mirror to watch the activities of the customers.
- Road safety mirrors at turns on the roads, for a driver to watch the vehicles approaching from the other side.


Summary
1. The incident ray, the normal and the reflected ray all lie in the same plane.
2. The angle of incidence and Angle of reflection are always equal.
3. f=r/2, both f, and r are positive for concave mirror and negative for convex mirror.
4. Mirror formula for any type of mirror:
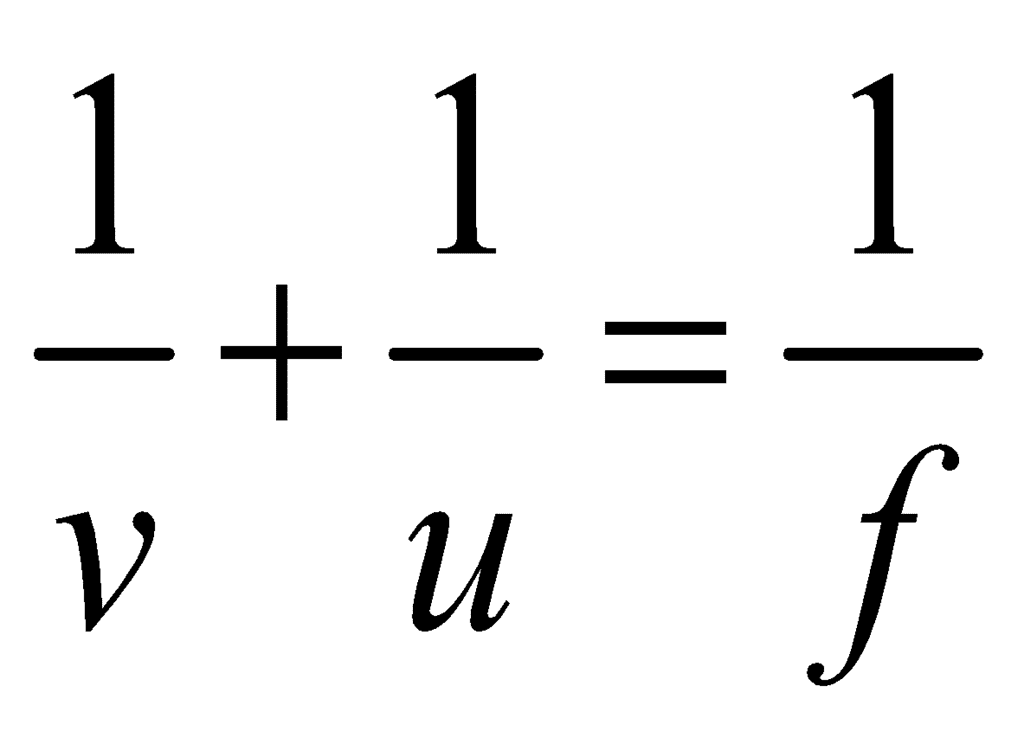
5. Magnification of a mirror is given by:
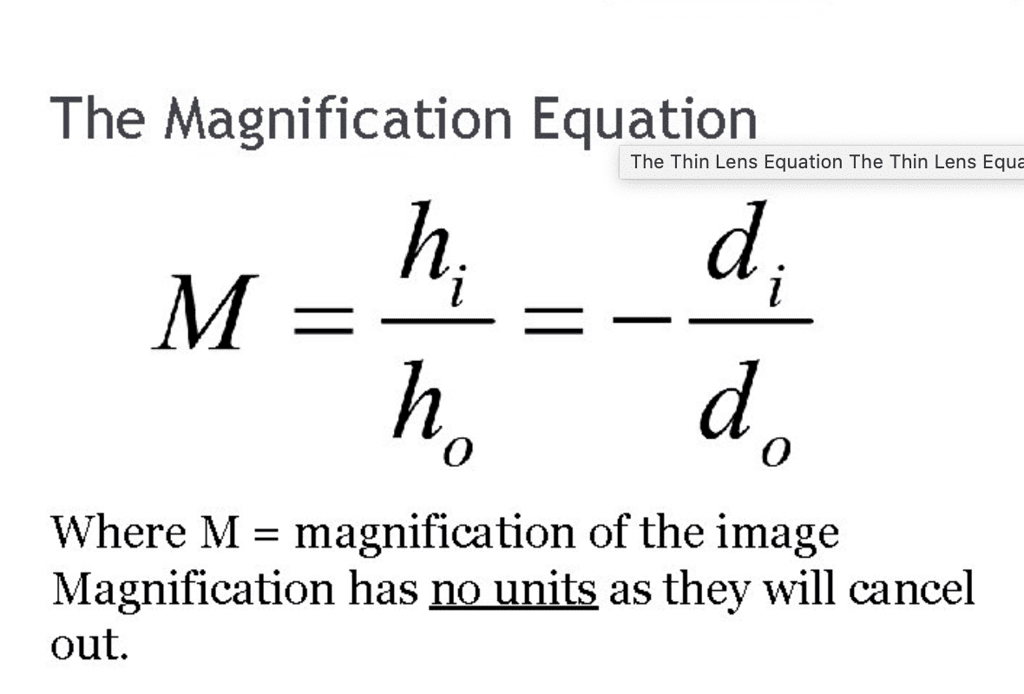
where hi is the height of the image, ho is the height of the object, di is the distance of the image from the pole, and do is the distance of the object from the pole.
Important Questions for Exam
Q.1. The magnification of ‘X’ is more than unity. Identify X.
a) Convex mirror
b) Concave mirror
c) Plane mirror
d) Prism
Answer: b
Explanation: If the magnification of the mirror is one, then it is a plane mirror. If magnification is more than one, the mirror is concave. If magnification is less than one, then the mirror is convex. So the X required in this question is a concave mirror.
Q.2. Which of the following causes refraction of light?
a) Change in the density of light from one medium to another
b) Change in viscosity of light from one medium to another
c) Change in the speed of light from one medium to another
d) Change in direction of light from one medium to another
Answer: c
Explanation: Light travels at different speeds in a different medium. The bending or refraction of light occurs due to the change in the speed of light as it passes from one medium to another. Other statements are not true regarding the refraction of light.
Q.3. If a concave mirror of focal length 10cm is immersed in water, its focal length will ________.
a) Be reduced
b) Be increased
c) Remain unchanged
d) More than one of the above
e) None of the above
Answer: The correct answer is to Remain unchanged.
Explanation: In the case of mirrors, for both concave and convex the focal length shall remain unchanged for the mirrors when immersed in water.
Q.4. As the object moves towards the plane mirror the size of the image:
a) Increases
b) Decreases
c) Remain unchanged
d) Can't say
e) None of the above/More than one of the above.
Answer 3 : Remain unchanged
Explanation:
- As we know that for the plane mirror the size of the image formed is the same as the size of the object for all positions of the object.
- So as the object moves towards the plane mirror the size of the image will always be equal to the size of the object.
- Therefore the size of the image remains unchanged. Hence, option 3 is correct.
Q.5. The magnification of ‘X’ is more than unity. Identify X.
a) Convex mirror
b) Concave mirror
c) Plane mirror
d) Prism
Answer: b
Explanation: If the magnification of the mirror is one, then it is a plane mirror. If magnification is more than one, the mirror is concave. If magnification is less than one, then the mirror is convex. So the X required in this question is a concave mirror.
|
74 videos|314 docs|88 tests
|
FAQs on Types of Mirrors, Mirror Formula and Applications - Physics Class 12 - NEET
| 1. What is a mirror and how does it work? |  |
| 2. What are the properties related to a plane mirror? |  |
| 3. What is the mirror formula for concave and convex mirrors? |  |
| 4. How is magnification defined in the context of mirrors? |  |
| 5. What are some applications of spherical mirrors? |  |