Introduction to Atomic Structure: Various Models of Atom | Physical Chemistry PDF Download
| Table of contents |

|
| Atomic Structure: Discovery of Subatomic Particles |

|
| Dalton’s Theory of Atoms |

|
| Various Models of Atom |

|
| Bohr’s Atomic Model |

|
Atomic Structure: Discovery of Subatomic Particles
Atomic structure refers to the structure of an atom comprising a nucleus (centre) in which protons (positively charged) and neutrons (neutral) are present. Negatively charged particles called electrons revolve around the centre of the nucleus.
- The history of atomic structure and quantum mechanics dates back to the times of Democritus, the man who first proposed that matter is composed of atoms.
- The study of the structure of an atom gives great insight into the entire class of chemical reactions, bonds, and their physical properties.
- The first scientific theory of atomic structure was proposed by John Dalton in the 1800s.
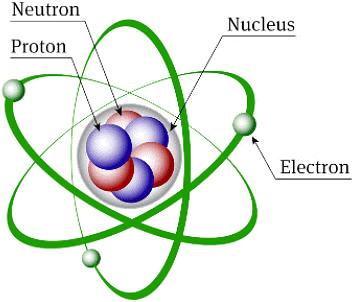 Structure of Atom
Structure of Atom
Dalton’s Theory of Atoms
According to this theory the Atom is considered to be the hardest, densest, and smallest particle of matter that is indivisible. The atoms belonging to a particular element, are unique.
Main Postulates of Dalton's Atomic Theory:
- Atoms are the smallest units of matter and cannot be divided, created, or destroyed.
- All atoms of the same element have identical mass and properties.
- Atoms of different elements combine in fixed, whole-number ratios to form compounds.
- Atoms are rearranged in chemical reactions, but no new atoms are created or destroyed.
- Atoms of different elements have unique properties.
Drawbacks of Dalton's Theory of Atoms
- Discovery of electrons, protons, and neutrons showed that atoms are divisible.
- Atoms of the same element can have different masses (isotopes), challenging the idea that all atoms of an element are identical.
- Atoms can be transformed in nuclear reactions, contradicting their indestructibility.
Dalton’s theory was groundbreaking and provided the foundation for modern atomic models, despite its limitations.
Sub-Atomic Particles
The discovery of various sub-atomic particles like electrons, protons, etc. during the late 19th century led to the idea that the atom was no longer an indivisible, small particle of matter.
Characteristics of the three fundamental particles are: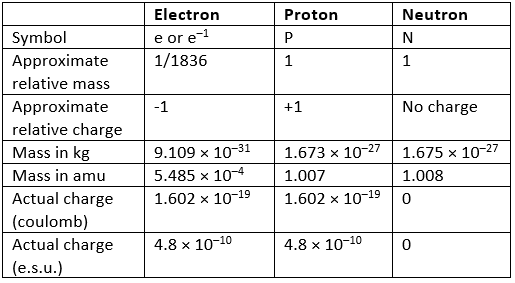
Atomic Mass Unit: The atomic mass unit (amu) is 1/12 of the mass of an individual atom of 6C12, i.e., 1.660 × 10h – 27 kg. The neutron and proton have approximately equal masses of 1 amu and the electron is about 1836 times lighter. Its mass can sometimes be neglected as an approximation.
The electron and proton have an equal, but opposite, electric charges while the neutron is not charged.
Various Models of Atom
The models of the atom have evolved over time as scientists made more discoveries about the structure and behavior of atoms. Here's a major atomic models:
Thomson’s Model of Atom
Thomson assumed that an atom is a sphere of positive charges uniformly distributed, with the electrons scattered as points throughout the sphere.
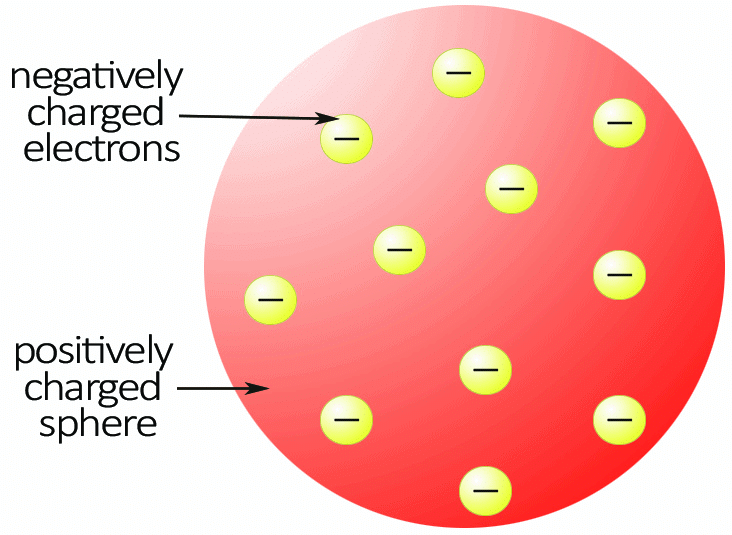
- This was known as the "plum pudding model" at that time.
- However, this idea was dropped due to the success of the a-particle scattering experiments studied by Rutherford and Marsden.
- Limitations: Couldn’t explain the results of the later gold foil experiment, where most of the alpha particles passed through the atom, implying the atom has a dense, positively charged nucleus
Rutherford’s Model of Atom
Rutherford's model of the atom describes that the atom is composed of an atomic nucleus and electrons surrounding the nucleus. This model caused to reject the Thomson model of atom.
- Alpha-particle emitted by radioactive substances was shown to be dipositive Helium ions (He++) having a mass of 4 units and 2 units of positive charge.
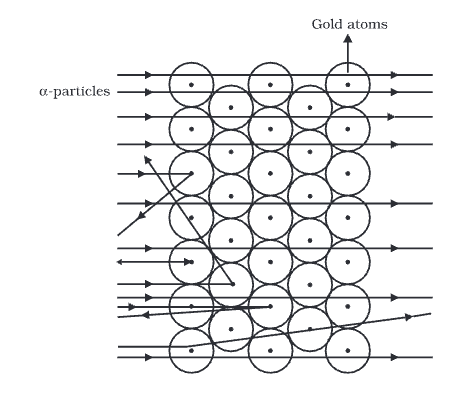
- Rutherford allowed a narrow beam of α-particles to fall on a very thin gold foil of a thickness of the order of 4 × 10–4 cm and determined the subsequent path of these particles with the help of a zinc sulfide fluorescent screen.
- This zinc sulfide screen gives off a visible flash of light when struck by an α-particle, as ZnS has the remarkable property of converting the kinetic energy of particles into visible light.
Observation
- The majority of the α-particles pass straight through the gold strip with little or no deflection.
- Some particles are deflected from their path and diverge.
- Very few particles are deflected backwards through angles greater than 90°
- Some were ever scattered in the opposite direction at an angle of 180°
 Rutherford's Experiment
Rutherford's Experiment
Conclusion
- The fact that most of the a-particles passed straight through the metal foil indicates that most part of the atom is empty.
- The fact that few alpha-particles are deflected at large angles indicates the presence of a heave positively charged body i.e., for such large deflections to occur a-particles must have some closer to or collide with a massive positively charged body, and he named its nucleus.
- The fact that one in 20,000 have deflected at 180° backward indicates that the volume occupied by this heavy positively charged body is very small in comparison to the total volume of the atom
Drawbacks of Rutherford’s Atomic Model
- Position of electrons: The exact positions of the electrons from the nucleus are not mentioned.
- Stability of the atom: Neils Bohr pointed out that Rutherford’s atom should be highly unstable. According to the law of electrodynamics, the electron should, therefore, continuously emit radiation and lose energy. As a result of this, a moving electron will come closer and closer to the nucleus and after passing through a spiral path, it should ultimately fall into the nucleus.
- It was calculated that electrons should fall into the nucleus in less than 10–8 sec. But it is known that electrons keep moving outside the nucleus.
- To solve this problem Neils Bohr proposed an improved form of Rutherford’s atomic model.
Before going into the details of the Neils Bohr model let's understand some important terms.
An absorption spectrum occurs when light passes through a substance, and specific wavelengths are absorbed, creating dark lines in the spectrum. These lines correspond to energy transitions in the substance's atoms or molecules, and each element has a unique absorption spectrum.
Dark Line in Absorption Spectrum
If the atom gains energy the electron passes from a lower energy level to a higher energy level, energy is absorbed which means a specific wavelength is absorbed. Consequently, a dark line will appear in the spectrum. This dark line constitutes the absorption spectrum.
Hydrogen Atom
When electric discharge passes through hydrogen gas, it emits a line spectrum with sharp lines in the UV, visible, and IR regions. The visible lines are seen on photographic film. This spectrum consists of six series named after their discoverers: Lyman, Balmer, Paschen, Brackett, Pfund, and Humphrey. Each series corresponds to specific wavelengths, and the wavelengths can be described by a single formula.
= wave number
l = wave length
R = Rydberg constant (109678 cm–1)
n1 and n2 have integral values as follows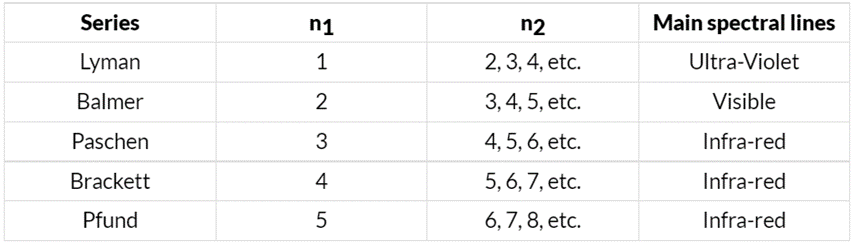
Types of Emission Spectra:
Continuous Spectrum: Produced when white light (e.g., sunlight or light from a bulb) is passed through a prism. The light splits into a continuous range of colors, from violet to red, without any gaps.
Example: Rainbow or sunlight.
Line Spectrum: Produced when light is emitted by a gas at low pressure (e.g., through electric discharge). This spectrum consists of distinct, isolated colored lines separated by dark spaces. Each line corresponds to a specific wavelength of light emitted by the gas. Each element has a unique line spectrum.
Example: Spectra of hydrogen or other elements.
Planck’s Quantum Theory
When a black body is heated, it emits thermal radiation of different wavelengths or frequencies. To explain these radiations, Max Planck put forward a theory known as Planck’s theory. The main points of quantum theory are:
- Substances radiate or absorb energy discontinuously in the form of small packets or bundles of energy.
- The smallest packet of energy is called quantum. In the case of light, the quantum is known as a photon.
- The energy of a quantum is directly proportional to the frequency of the radiation. E∝ ν ( or E= hv where v is the frequency of radiation and h is Planck’s constant having the value 6.626 × 10–27 erg-sec or 6.626 × 10–34 J-sec.
- A body can radiate or absorb energy in whole-number multiple of a quantum hv, 2hv, 3hv, nhν where n is the positive integer. Nelis Bohr used this theory to explain the structure of atoms.
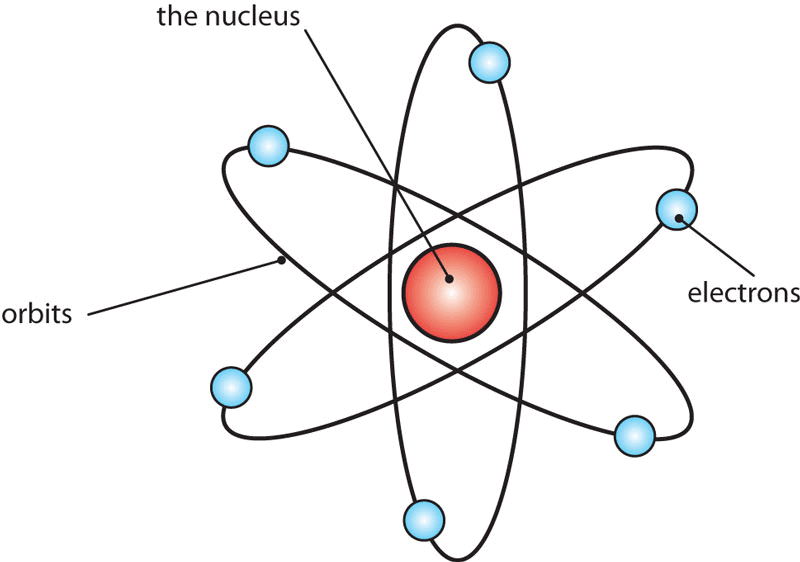
Bohr’s Atomic Model
Bohr developed a model for hydrogen and hydrogen-like atoms one-electron species (hydrogenic species). He applied quantum theory in considering the energy of an electron bound to the nucleus.
 Bohr's Model of an Atom
Bohr's Model of an Atom
Postulates of Bohr's Model
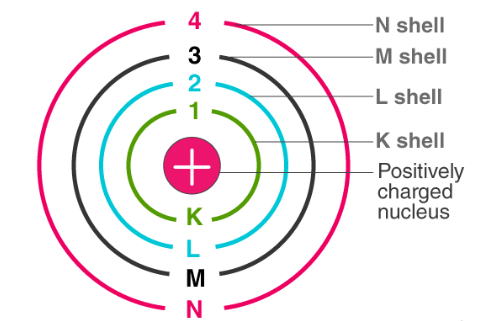
- An atom consists of a dense nucleus situated at the center with the electron revolving around it in circular orbitals without emitting any energy. The force of attraction between the nucleus and an electron is equal to the centrifugal force of the moving electron.
- In an atom, electrons (negatively charged) revolve around the positively charged nucleus in a definite circular path called orbits or shells.
- Of the finite number of circular orbits possible around the nucleus, the electron can revolve only in those orbits whose angular momentum (mvr) is an integral multiple of factor h/2p.
Where m = mass of the electron
v = velocity of the electron
n = orbit number on which electron is present
r = radius of the orbit - The energy levels are represented by an integer (n=1, 2, 3…) known as the quantum number. This range of quantum number starts from nucleus side with n=1 having the lowest energy level. The orbits n=1, 2, 3, 4… are assigned as K, L, M, N…. shells and when an electron attains the lowest energy level, it is said to be in the ground state.
- The electrons in an atom move from a lower energy level to a higher energy level by gaining the required energy and an electron moves from a higher energy level to lower energy level by losing energy.
- Energy absorbed or released in an electron jump, (ΔE) is given by ΔE = E2 – E1 = hv
Where E2 and E1 are the energies of the electron in the first and second energy levels, and v is the frequency of radiation absorbed or emitted.
Merits of Bohr’s theory
- The experimental value of radii and energies in a hydrogen atom is in good agreement with that calculated on the basis of Bohr’s theory.
- Bohr’s concept of the stationary state of electrons explains the emission and absorption spectra of hydrogen-like atoms.
- The experimental values of the spectral lines of the hydrogen spectrum are in close agreement with the calculated by Bohr’s theory.
Limitations of Bohr’s Theory
- Only for Hydrogen: It only explained hydrogen’s spectrum, not multi-electron atoms.
- Electron Behavior: It treated electrons as particles in fixed orbits, ignoring their wave nature.
- Lack of Quantum Mechanics: It didn't fully incorporate quantum mechanics.
- Zeeman and Stark Effects: Couldn't explain line splitting in magnetic or electric fields.
- Fixed Orbits: Electrons don’t follow fixed orbits; they exist in probabilistic orbitals.
- Fine Structure: It couldn’t explain the fine structure of spectral lines in complex atoms.
Results of Bohr's Theory:
Radius and Energy levels of the hydrogen atom
Consider an electron of mass ‘m’ and charge ‘e’ revolving around a nucleus of charge Ze (where Z = atomic number and e is the charge of the proton) with a tangential velocity v.r is the radius of the orbit in which electron is revolving.
By Coulomb’s Law, the electrostatic force of attraction between the moving electron and nucleus is
Coulombic force =
(where ε0 is the permittivity of free space)
K = 9 × 109 Nm2C–2
In C.G.S units, value of K = 1 dyne cm2 (esu)–2
The centrifugal force acting on the electron is
Since the electrostatic force balance the centrifugal force, for the stable electron orbit.
...............(i)
...............(ii)
According to Bohr’s postulate of angular momentum quantization, we have
............ (iii)
Equating (ii) and (iii)
Solving for r we get r =
Where n = 1, 2, 3, ………….∞
Hence only certain orbits whose radii are given by the above equation are available for the electron. The greater the value of n, i.e., the farther the level from the nucleus the greater is the radius.
The radius of the smallest orbit (n = 1) for the hydrogen atom (Z = 1) is
r0 = 0.529 Å
The radius of nth orbit for an atom with atomic number Z is simply written as
Illustration: Calculate the ratio of the radius of Li+2 ion in 3rd energy level to that of He+ ion in 2nd energy level:
Solution:
n1 = 3
n2 = 3
z1 = 3 (for Li2+)
z2 = 2 (for He+)
The Energy Level of Hydrogen atom:
- The total energy, E of the electron is the sum of kinetic energy and potential energy. The kinetic energy of the electron = 1/2 mv2
- Potential energy =
- Total energy =
………..(4)
From equation (1) we know that
Substituting this in equation (4)
Total energy (e)
Substituting for r, gives us
Ewhere n 1, 2, 3.........
This expression shows that only certain energies are allowed to the electron. Since this energy expression consists of so many fundamental constants, we are giving you the following, simplified expressions.
E =erg per Atom
(1 eV = 3.83 × 10–23 Kcal)
(1 eV = 1.602 × 10–12 erg)
(1 eV = 1.602 × 10–19 J)kcal/mole (1cal = 4.18 J)
The energies are negative since the energy of the electron in the atom is less than the energy of a free electron (i.e., the electron is at an infinite distance from the nucleus) which is taken as zero. The lowest energy level of the atom corresponds to n = 1, and as the quantum number increases, E becomes less negative.
When n = ∞, E = 0 which corresponds to an ionized atom i.e., the electron and nucleus are infinitely separated. - Velocity of Electron:
We know that mvr =
By substituting for r we are getting
Where excepting n and z all are constant, v =
Further application of Bohr’s work was made, to other one-electron species (Hydrogenic ion) such as He+ and Li2+. In each case of this kind, Bohr’s prediction of the spectrum was correct.
|
90 videos|144 docs|67 tests
|
FAQs on Introduction to Atomic Structure: Various Models of Atom - Physical Chemistry
| 1. What is Dalton's Theory of Atoms? |  |
| 2. What are the various models of the atom? |  |
| 3. What are subatomic particles? |  |
| 4. What is the Bohr atomic model? |  |
| 5. What are some important atomic terms? |  |





















