The Hydrogen Atom - Atomic Structure | Physical Chemistry PDF Download
THE HYDROGEN ATOM
Quantization of Electronic Energy:
Necessity of Repairing Bohr’s theory:
The mathematical framework of the Bohr’s theory was based on the basic assumption of quantization of orbital angular momentum of the electron. It was seen earlier that this theory led to the quantization of electronic energies which formed the basis for explaining the experimental spectra of hydrogen like species such as H, He+, Li2+, and Be3+. However, this theory was not entirely satisfactory as it failed to provide an interpretation of relative line intensities in the hydrogen spectrum and also failed completely when it was applied to explain the energies and spectra of more complex atoms. In this section, we consider the application of Schrodinger’s wave theory to one-electron atom. In the subsequent section, it will be shown how the principles of this theory can be applied, in a more approximate way, to many electron atoms.
Setting of Schrodinger Equation:
The time independent form of Schrodinger equation is
...........(1) Where Hop is the Hamiltonian operator, Etotal is the total nonrelativistic energy and
is the wave function for the total system. Since the hydrogen like system contain two particles, namely, nucleus and electron, it is obvious that wave function
depends on the six coordinate variables, three for the electron xe, ye, ze and three for the nucleus xn, yn, zn , both sets of coordinates refer to the common origin. The Hamiltonian operator consists of two terms, viz. the kinetic and potential energy terms. The kinetic energy operator will contain two terms, one for the electron and one for the nucleus. Thus, we have
...........(2)
All symbols have their usual meanings, Substituting Eq. 1, have
..............(3)
Equation 3 can be broken into two simpler equations, one involving the free movement of the centre of mass of the atom in space and the other involving the relative motion of the electron with respect to the nucleus within the atom. the two equations are
............(4)
and
.........(5)
with Etrans + E = Etotal
Equation (4) is simply the Schrodinger equation for a particle of mass (me + mn) , Etrans is the translational kinetics energy associated with the free movement of the centre of mass of the atom through space. Equation 5 is the Schrodinger equation which represents the system in which an electron of reduced mass μ is revilving around the stationary nucleus of positive charge Z at a distance of r. The behavior of this electron can be described by the function ψe and E is the corresponding energy of the electron. The allowed values of electronic energies can be obtained by solving Equation 5 Equation 4 which describes the motion of the centre of mass is of the form as that of the particle in a three dimensional box.
Schrodinger Equation in Terms of Spherical Polar Coordinates:
The solution of Schrodinger equation becomes very much simplify if the equation is expressed in the coordinate system that reflects the symmetry of the system. In the present case the potential energy field is spherical symmetry (V depends only on r), and thus, it is convenient to case the Schrodinger equation 5 into the spherical polar coordinates, θ and φ by using the relations
The transformation is length and tedious process, and only the transformed expression is given below:
Where ψ is a function of r, θ and φ
Splitting of Schrodinger Equation: Rearranging the above expression, we get
Multiplying throughout by r2 and rearranging the resulrant expression, we get
..........(6)
Since the operator is made up of two terms, one depending on the variable r and the other on the variables θ and φ taken together, we can write the wave function ψ as the product of two functions- one depending on r and the other on θ and φ. Hence, we can write
............(7)
The function Y is known as spherical harmonics. Substituting Equation 7 in equation 6 we get
...................(8)
Dividing throughout by Rr Yθ.φ, we get
............(9)
Equality shown in equation (9) holds good only when both sides are equal to a constant say, ℓ (ℓ + 1). Thus equation (9) separates into two equations, one depending only one and other on and φ. These are:
Equation involving the variable r
..........(10)
Equation involving the angles θ and φ
...............(11)
Multiplying equation (1) by sin2 θ and rearranging the resultant expression, we get
..............(12)
Since the operator in equation (11) consists of two terms. One depending on θ and other on φ, we can write the wave function (12) becomes
Dividing throughout by and rearranging, we get
..........(13)
The two sides of equation (12) must be equal to a constant, say m2. Thus, we have
................(14)
And ................(15)
Three Split Expressions of the Schrodinger Equation:
Thus, the Schrodinger equation (6) for the hydrogen like species can be separated into three equations. These are:
- Equation involving only r
...............(16)
- Equation involving only θ
...............(17)
- Equation involving only φ
................(18)
We now consider the acceptable solutions of Equations (16), (17) and (18).
Solutions of φ Dependent Equation:
Equation (17) has already been solved in connection with the rigid rotator system. Its solution is
...............(19)
The constant m is called the magnetic quantum number and it represents the quantization of the z-component of the angular momentum since
...............(20)
Thus, the permitted values of z-component of the angular momentum of the electron are given by the expression m(h/2π).
Solutions of θ-Dependent Equation:
Equation (17) has also been solved in the rotator system. The solution is
.............(21)
Where:Associated legendre polynominals ............(22)
: legendre polynominals ............(23)
And
These solutions are obtained provided the following conditions are satisfied.
The quantum number l is called the azimuthal quantum or the subsidiary quantum number and it represents the quantization of the square of total angular momentum according to the equation
..............(24)
Solution of r-Dependent Equation:
With the help of a suitable transformation of independent variable and from the forms of solutions as the variable approaches zero and infinity, it is possible to write in the following more familiar form, known as associated laguerre equation.
.............(25)
Where the function R is related to the function L through the following transformation scheme.
..............(26)
The terms ρ,j and k are given by
..............(27)
..............(28)
..............(29)
Where .............(30)
..............(31)
The solution of Equation (25). as determined by the power series method, is the associated laguerre polynomial of degree (k-j) and order j, and is given by
...................(32)
Where Lk, the laguerre polynomial of degree k, is given by
...................(33)
In order that the association laguerre polynomial is the acceptable solution of equation (25) the following quantum restriction has to be satisfied.
k = 1,2,3,................∞...................(34)
Acceptable solutions, as usual, means that the wave function L (ρ) should be a well-behaved function and should vanish as ρ→∞. The later condition that the polynomial must be restricted to a finite number of terms.
This quantum restriction leads to the fact that λ which is equal to K-t(eq. 29) must also be an integer. Let λ be written as n, so that
k = n + 1...................(35 )
Expression of the Normalized R Function:
Thus, the function R as given by Equation (26) is
...................(36)
Normalizing the above solution through the expression
We get ...................(37)
Where ...................(38)
And ...................(39)
Allowed Values of n and its Relation with I:
The constant is referred to as the principal quantum number. If the associated Laguerre polynomial (Eq32) is not to vanish, we must have
j≤k …(40)
j2ℓ + 1 and k = n + ℓ, we have
Since (2ℓ + 1) ≤ (n + ℓ )
Or ℓ + 1 ≤ n ℓ ≤ n - 1...................(41)
Since the allowed values of are 1,2,3,….,it is obvious that the principal quantum number n cannot have a zero value. The allowed values of n are only positive integers. Thus, we have
n = 1,2,3.4,.........
l = 0,1,2,3,.....,(n - 1).................(42)
Expressions for the Function Rn.ℓ:
The exact form of the function Rn.ℓ (r) for the given values of n and can be determined from Equations (37), (32) and (33). These equations are
...................(43)
...................(44)
And
Where ...................(45)
Spectral Lines of Hydrogen
Bohr’s model explains the spectral lines of the hydrogen atomic emission spectrum. While the electron of the atom remains in the ground state, its energy is unchanged. When the atom absorbs one or more quanta of energy, the electron moves from the ground state orbit to an excited state orbit that is further away. Energy levels are designated with the variable n. The ground state is n = 1, the first excited state is n = 2, and so on. The energy that is gained by the atom is equal to the difference in energy between the two energy levels. When the atom relaxes back to a lower energy state, it releases energy that is again equal to the difference in energy of the two orbits (see Figure 1).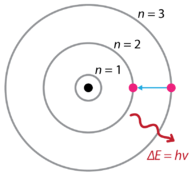 Figure 1. Bohr model of the atom: electron is shown transitioning from the n = 3 energy level to the n = 2 energy level. The photon of light that is emitted has a frequency that corresponds to the difference in energy between the two levels.
Figure 1. Bohr model of the atom: electron is shown transitioning from the n = 3 energy level to the n = 2 energy level. The photon of light that is emitted has a frequency that corresponds to the difference in energy between the two levels.
The change in energy, ΔE, then translates to light of a particular frequency being emitted according to the equation E = hv. Recall that the atomic emission spectrum of hydrogen had spectral lines consisting of four different frequencies. This is explained in the Bohr model by the realization that the electron orbits are not equally spaced. As the energy increases further and further from the nucleus, the spacing between the levels gets smaller and smaller.
Based on the wavelengths of the spectral lines, Bohr was able to calculate the energies that the hydrogen electron would have in each of its allowed energy levels. He then mathematically showed which energy level transitions corresponded to the spectral lines in the atomic emission spectrum ( Figure 2).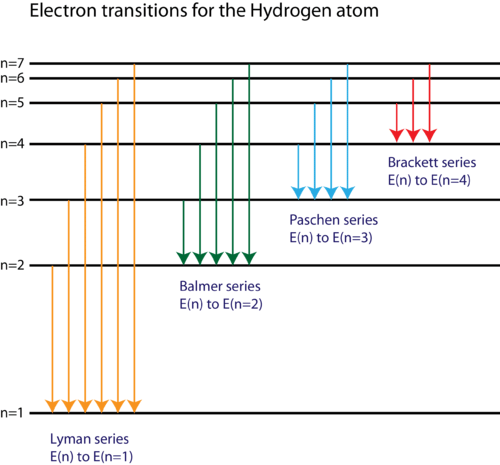 Figure 2. The electron energy level diagram for the hydrogen atom.
Figure 2. The electron energy level diagram for the hydrogen atom.
He found that the four visible spectral lines corresponded to transitions from higher energy levels down to the second energy level (n = 2). This is called the Balmer series. Transitions ending in the ground state (n = 1) are called the Lyman series, but the energies released are so large that the spectral lines are all in the ultraviolet region of the spectrum. The transitions called the Paschen series and the Brackett series both result in spectral lines in the infrared region because the energies are too small.
Bohr’s model was a tremendous success in explaining the spectrum of the hydrogen atom. Unfortunately, when the mathematics of the model was applied to atoms with more than one electron, it was not able to correctly predict the frequencies of the spectral lines. While Bohr’s model represented a great advancement in the atomic model and the concept of electron transitions between energy levels is valid, improvements were needed in order to fully understand all atoms and their chemical behavior.
Summary
- Emission lines for hydrogen correspond to energy changes related to electron transitions.
- The Bohr model works only for the hydrogen atom.
|
84 videos|142 docs|67 tests
|
FAQs on The Hydrogen Atom - Atomic Structure - Physical Chemistry
| 1. What is the atomic structure of a hydrogen atom? |  |
| 2. How is the hydrogen atom different from other atoms? |  |
| 3. What is the significance of the hydrogen atom in scientific research? |  |
| 4. How does the hydrogen atom emit light? |  |
| 5. How does the hydrogen atom contribute to the understanding of the universe? |  |





















