Loops in Flow Graph | Compiler Design - Computer Science Engineering (CSE) PDF Download
Loops in Flow Graph
A graph representation of three-address statements, called a flow graph, is useful for understanding code-generation algorithms, even if the graph is not explicitly constructed by a code-generation algorithm. Nodes in the flow graph represent computations, and the edges represent the flow of control.
Dominators
In a flow graph, a node d dominates node n, if every path from initial node of the flow graph to n goes through d. This will be denoted by d dom n. Every initial node dominates all the remaining nodes in the flow graph and the entry of a loop dominates all nodes in the loop. Similarly every node dominates itself.
Example:
In the flow graph below,
*Initial node,node1 dominates every node
*node 2 dominates itself
*node 3 dominates all but 1 and 2. *node 4 dominates all but 1,2 and 3.
*node 5 and 6 dominates only themselves, since flow of control can skip around either by goin through the other.
*node 7 dominates 7,8 ,9 and 10.
*node 8 dominates 8,9 and 10.
*node 9 and 10 dominates only themselves.

The way of presenting dominator information is in a tree, called the dominator tree, in which
• The initial node is the root.
• The parent of each other node is its immediate dominator.
• Each node d dominates only its descendents in the tree.
The existence of dominator tree follows from a property of dominators; each node has a unique immediate dominator in that is the last dominator of n on any path from the initial node to n. In terms of the dom relation, the immediate dominator m has the property is d=!n and d dom n, then d dom m.
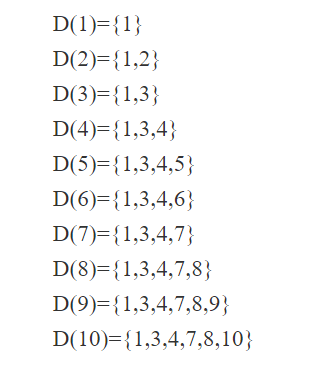
Natural Loops
One application of dominator information is in determining the loops of a flow graph suitable for improvement. There are two essential properties of loops:
A loop must have a single entry point, called the header. This entry point-dominates all nodes in the loop, or it would not be the sole entry to the loop.
There must be at least one way to iterate the loop(i.e.)at least one path back to the header. One way to find all the loops in a flow graph is to search for edges in the flow graph whose heads dominate their tails. If a→b is an edge, b is the head and a is the tail. These types of
edges are called as back edges.
Example: In the above graph,
7→4 4 DOM 7
10 →7 7 DOM 10
4→3
8→3
9 →1
The above edges will form loop in flow graph. Given a back edge n → d, we define the natural loop of the edge to be d plus the set of nodes that can reach n without going through d. Node d is the header of the loop.
Algorithm: Constructing the natural loop of a back edge
Input: A flow graph G and a back edge n→d.Output: The set loop consisting of all nodes in the natural loop n→d.
Method: Beginning with node n, we consider each node m*d that we know is in loop, to make sure that m’s predecessors are also placed in loop. Each node in loop, except for d, is placed once on stack, so its predecessors will be examined. Note that because d is put in the loop initially, we never examine its predecessors, and thus find only those nodes that reach n without going through d.
Procedure insert(m);
if m is not in loop then begin loop := loop U {m};
push m onto stack end;
stack : = empty;
loop : = {d}; insert(n);
while stack is not empty do begin
pop m, the first element of stack, off stack;
for each predecessor p of m do insert(p)
end
Inner Loops
If we use the natural loops as “the loops”, then we have the useful property that unless two loops have the same header, they are either disjointed or one is entirely contained in the other. Thus, neglecting loops with the same header for the moment, we have a natural notion of inner loop: one that contains no other loop. When two natural loops have the same header, but neither is nested within the other, they are combined and treated as a single loop.
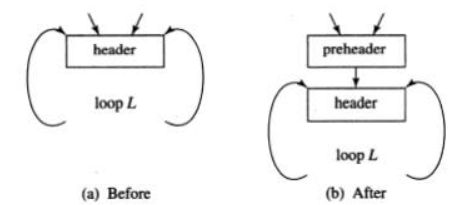
Pre-Headers
Several transformations require us to move statements “before the header”. Therefore begin treatment of a loop L by creating a new block, called the preheader. The pre-header has only the header as successor, and all edges which formerly entered the header of L from outside L instead enter the pre-header. Edges from inside loop L to the header are not changed. Initially the pre-header is empty, but transformations on L may place statements in it.

Reducible flow graphs
Reducible flow graphs are special flow graphs, for which several code optimization transformations are especially easy to perform, loops are unambiguously defined, dominators can be easily calculated, data flow analysis problems can also be solved efficiently. Exclusive use of structured flow-of-control statements such as if-then-else, while-do, continue, and break statements produces programs whose flow graphs are always reducible.
The most important properties of reducible flow graphs are that
1. There are no umps into the middle of loops from outside;
2. The only entry to a loop is through its header
Definition
A flow graph G is reducible if and only if we can partition the edges into two disjoint groups, forward edges and back edges, with the following properties.
- The forward edges from an acyclic graph in which every node can be reached from initial node of G.
- The back edges consist only of edges where heads dominate theirs tails.
|
26 videos|66 docs|30 tests
|
FAQs on Loops in Flow Graph - Compiler Design - Computer Science Engineering (CSE)
| 1. What is a loop in a flow graph? |  |
| 2. How are loops useful in flow graphs? |  |
| 3. What are the types of loops commonly found in flow graphs? |  |
| 4. How do loops impact the complexity of a flow graph? |  |
| 5. How can loops be optimized in a flow graph to improve performance? |  |

|
Explore Courses for Computer Science Engineering (CSE) exam
|

|


















