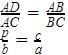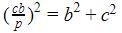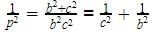RS Aggarwal Test: Triangles - Grade 10 MCQ
17 Questions MCQ Test - RS Aggarwal Test: Triangles
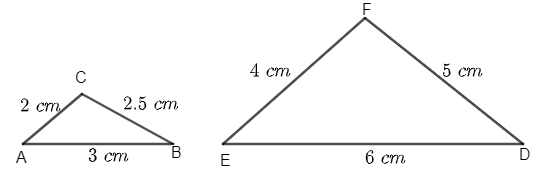
Triangle ABC is such that AB = 3 cm, BC = 2 cm and CA = 2.5 cm. Triangle DEF is similar to ΔABC. If EF = 4 cm, then the perimeter of ΔDEF is :
In ΔABC, AB = 3 cm, AC = 4 cm and AD is the bisector of ∠A. Then, BD : DC is :
ABC is a triangle and DE is drawn parallel to BC cutting the other sides at D and E. If AB = 3.6 cm, AC = 2.4 cm and AD = 2.1 cm, then AE is equal to :
The line segments joining the mid points of the sides of a triangle form four triangles each of which is :
In ΔABC and ΔDEF, ∠A = 50°, ∠B = 70°, ∠C = 60°, ∠D = 60°, ∠E = 70°, ∠F = 50°, then ΔABC is similar to:
If in the triangles ABC and DEF, angle A is equal to angle E, both are equal to 40°, AB : ED = AC : EF and angle F is 65°, then angle B is :-
In a right angled ΔABC, right angled at A, if AD ⊥ BC such that AD = p, If BC = a, CA = b and AB = c, then:
The ratio of the corresponding sides of two similar triangles is 1 : 3. The ratio of their corresponding heights is :
In a triangle ABC, if AB, BC and AC are the three sides of the triangle, then which of the statements is necessarily true?
In the adjoining figure D is the midpoint of BC of a ΔABC. DM and DN are the perpendiculars on AB and AC respectively and DM = DN, then the ΔABC is :
Triangle ABC is such that AB = 9 cm, BC = 6 cm, AC = 7.5 cm. Triangle ΔDEF is similar to ABC, If EF = 12 cm then DE is :
In ΔABC, AB = 5 cm, AC = 7 cm. If AD is the angle bisector of ∠A. Then BD : CD is:
In a ΔABC, D is the mid-point of BC and E is mid-point of AD, BF passes through E. What is the ratio of AF : FC?
The difference between altitude and base of a right angled triangle is 17 cm and its hypotenuse is 25 cm. What is the sum of the base and altitude of the triangle is ?
If AB, BC and AC be the three sides of a triangle ABC, which one of the following is true?