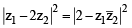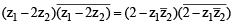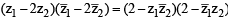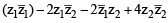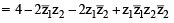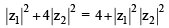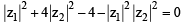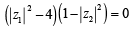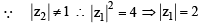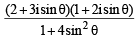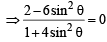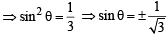Test: JEE Main 35 Year PYQs- Complex Numbers - JEE MCQ
25 Questions MCQ Test - Test: JEE Main 35 Year PYQs- Complex Numbers
z and w are two nonzero complex numbers such that | z | = | w| and Arg z + Arg w = π then z equals [2002]
If | z – 4 | < | z – 2 |, its solution is given by [2002]
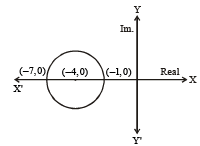
The locus of the centre of a circle which touches the circle | z – z1 | = a and | z – z2 | = b externally (z , z1 & z2 are complex numbers) will be [2002]
If z and ω are two non-zero complex numbers such that zω = 1 and Arg(z) - Arg(ω) = 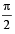 , then
, then 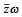 is equal to [2003]
is equal to [2003]
Let Z1 and Z 2 be two roots of the equation Z2 + aZ +b= 0 , Z being complex. Further , assume that the origin, Z1 and Z2 form an equilateral triangle. Then [2003]
Let z and w be complex numbers such that 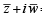 = 0 and arg zw = π. Then arg z equals [2004]
= 0 and arg zw = π. Then arg z equals [2004]
If z = x- iy and 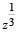 = p+ iq, then
= p+ iq, then 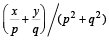 is equal to [2004]
is equal to [2004]
If | z2 - 1 |=|z |2+1, then z lies on [2004]
If the cube roots of unity are 1,ω ,ω2 then the roots of the equation ( x – 1)3 + 8 = 0, are [2005]
If z1 and z2 are two non- zero complex numbers such that | z1 +z2| = | z1| + | z2| , then arg z1 – arg z2 is equal to [2005]
If 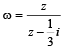 and |w| = 1, then z lies on [2005]
and |w| = 1, then z lies on [2005]
If z2 +z + 1=0 , where z is complex number, then the value of
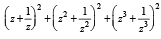
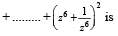
[2006]
If | z + 4 | ≤ 3, then the maximum value of | z + 1 | is[2007]
The conjugate of a complex n umber 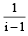 then that complex number is [2008]
then that complex number is [2008]
Let R be the real line. Consider the following subsets of the plane R × R:
S ={(x, y): y = x + 1 and 0 < x < 2}
T ={(x, y): x – y is an integer},
Which one of the following is true? [2008]
The number of complex numbers z such that |z – 1| = |z + 1| = |z – i| equals [2010]
Let α, β be real and z be a complex number. If z2 + αz + β = 0 has two distinct roots on the line Re z =1, then it is necessary that :[2011]
If ω(≠1) is a cube root of unity, and (1 + ω)7 = A +Bω.Then (A, B) equals [2011]
If z ≠ 1 and 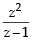 is real, then the point represented by the complex number z lies : [2012]
is real, then the point represented by the complex number z lies : [2012]
If z is a complex number of unit modulus and argument θ, then arg 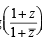 equals: [JEE M 2013]
equals: [JEE M 2013]
If z is a complex number such that z ≥ 2, then the minimum value of 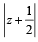
A complex number z is said to be unimodular if |z| = 1.
Suppose z1 and z2 are complex numbers such that 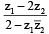 is unimodular and z2 is not unimodular. Then the point z1 lies on a: [JEE M 2015]
is unimodular and z2 is not unimodular. Then the point z1 lies on a: [JEE M 2015]
A value of θ for which 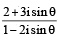 is purely imaginary, is: [JEE M 2016]
is purely imaginary, is: [JEE M 2016]


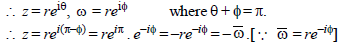

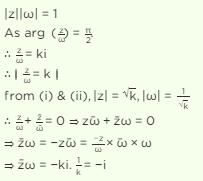
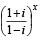 = 1 then [2003]
= 1 then [2003]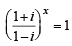 ⇒
⇒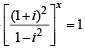
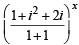 = ⇒ (i)x = 1;
= ⇒ (i)x = 1; 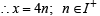
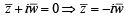
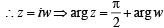
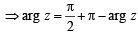
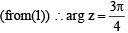
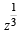 = p+ iq ⇒ z = p3 + (iq)3 + 3 p (iq)( p+ iq)
= p+ iq ⇒ z = p3 + (iq)3 + 3 p (iq)( p+ iq)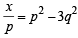
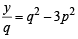
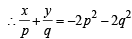
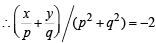
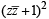
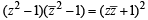

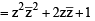
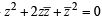 ⇒
⇒ 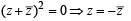
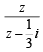 ⇒ |w| =
⇒ |w| = 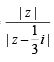 = 1
= 1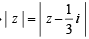
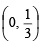 is
is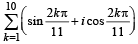 is [2006]
is [2006]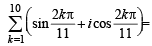
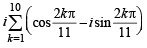
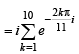
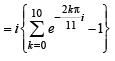
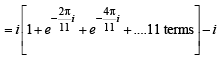
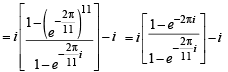
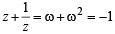
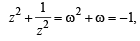
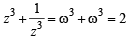
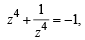
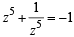 and
and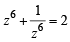
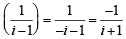
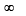 )
)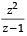 is real ⇒ Im
is real ⇒ Im 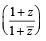 = 0
= 0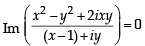
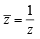
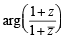
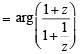 = arg (z) = θ
= arg (z) = θ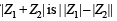
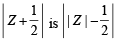
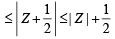
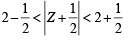
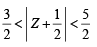
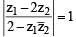 ⇒
⇒