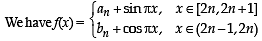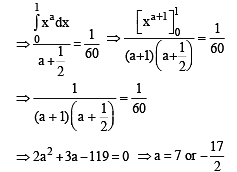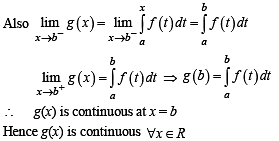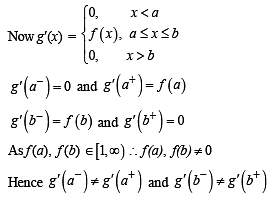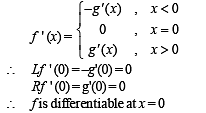Test: MCQs (One or More Correct Option): Limits, Continuity and Differentiability | JEE Advanced - JEE MCQ
25 Questions MCQ Test - Test: MCQs (One or More Correct Option): Limits, Continuity and Differentiability | JEE Advanced
If x+ | y | = 2y , then y as a function of x is
| 1 Crore+ students have signed up on EduRev. Have you? Download the App |
The function f (x) = 1 + | sin x | is
Let [x] denote the greatest integer less than or equal to x. If f(x) = [x sin π x], then f(x) is
The set of all points where the function  differentiable, is
differentiable, is
The function 
 then on the interval [0, π]
then on the interval [0, π]
The value of 
The following functions are continuous on (0, π).

Let g(x) = x f(x), where 
The function f(x) = max {(1 – x), (1 + x), 2}, x ∈ ( -∞,∞) is
Let h(x) = min {x, x2}, for every real number of x, Then
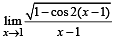
If f(x) = min {1, x2, x3}, then
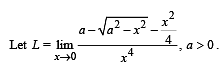
If L is finite, then
Let f : R → R be a function such that f (x + y) = f (x) + f (y), 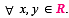 If f (x) is differentiable at x = 0, then
If f (x) is differentiable at x = 0, then

For every integer n, let an and bn be real numbers. Let function f : IR → IR be given by

for all integers n. If f is continuous, then which of the following hold(s) for all n ?
 (the set of all real numbers), a ≠ –1,
(the set of all real numbers), a ≠ –1,

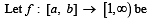 a continuous function and let g : R → R be defined as
a continuous function and let g : R → R be defined as

For every pair of continuous functions f, g : [0, 1] → R such that max {f ( x) :x ∈[ 0,1]} = max {g (x) :x ∈[ 0,1]} , the correct statement(s) is (are):
Let g : R → R be a differentiable function with g(0) = 0, g'(0) = 0 and g'(1) ≠ 0. Let 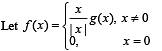 and
and  Let (foh)(x) denote f(h(x)) and (hof)(x) denote h(f(x)). Then which of the following is (are) true?
Let (foh)(x) denote f(h(x)) and (hof)(x) denote h(f(x)). Then which of the following is (are) true?
Let  be defined by f (x) = a cos (|x3 –x|) + b |x| sin (|x3 +x|).
be defined by f (x) = a cos (|x3 –x|) + b |x| sin (|x3 +x|).
Then f is
 be fun ctions defined by f (x) = [x2–3] and g(x) = |x| f (x) + |4x–7 | f (x), where [y] denotes the greatest integer less than or equal to y for y ∈ R. Then
be fun ctions defined by f (x) = [x2–3] and g(x) = |x| f (x) + |4x–7 | f (x), where [y] denotes the greatest integer less than or equal to y for y ∈ R. Then








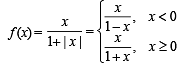
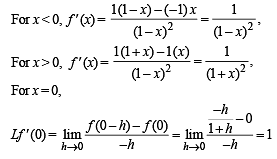


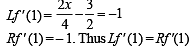



 are discontinuous on the interval [0, π].
are discontinuous on the interval [0, π].
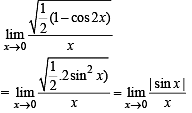



 which exists on (0, π)
which exists on (0, π)
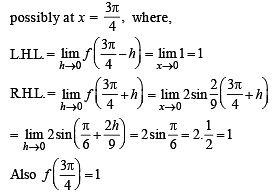




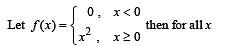






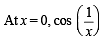 is not continuous, therefore g' (x) is not continuous at x = 0.
is not continuous, therefore g' (x) is not continuous at x = 0.


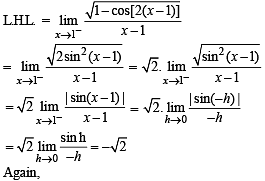

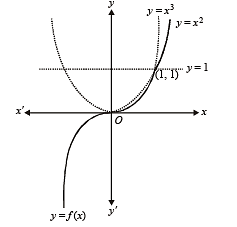





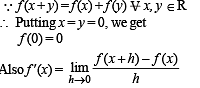
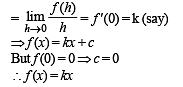



 which is differentiable.
which is differentiable.