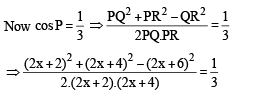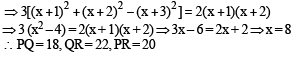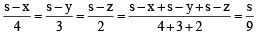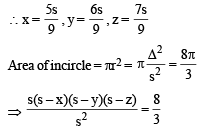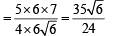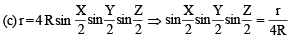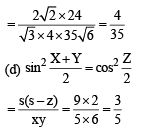Test: MCQs (One or More Correct Option): Properties of Triangle | JEE Advanced - JEE MCQ
8 Questions MCQ Test - Test: MCQs (One or More Correct Option): Properties of Triangle | JEE Advanced
There exists a triangle ABC satisfying the conditions
In a triangle, the lengths of the two larger sides are 10 and 9, respectively. If the angles are in A P. Then the length of the third side can be
| 1 Crore+ students have signed up on EduRev. Have you? Download the App |
If in a triangle PQR, sin P, sin Q, sin R are in A.P., then
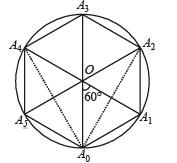
Let A0A1A2A3A4A5 be a regular hexagon inscribed in a circle of unit radius. Then the product of the lengths of the line segments A0A1,A0A2 and A0A4 is
In ΔABC, internal angle bisector of ∠A meets side BC in D. DE ⊥ AD meets AC in E and AB in F. Then
Let ABC be a triangle such that 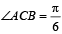 and let a, b and c denote the lengths of the sides opposite to A, B and C respectively. The value(s) of x for which a = x2 + x + 1, b = x2 – 1 and c = 2x + 1 is (are)
and let a, b and c denote the lengths of the sides opposite to A, B and C respectively. The value(s) of x for which a = x2 + x + 1, b = x2 – 1 and c = 2x + 1 is (are)
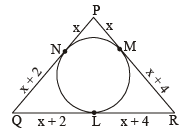
In a triangle PQR, P is the largest angle and cos p = 1/3. Further the incircle of the triangle touches the sides PQ, QR and RP at N, L and M respectively, such that the lengths of PN, QL and RM are consecutive even integers. Then possible length(s) of the side(s) of the triangle is (are)
In a triangle XYZ, let x, y, z be the lengths of sides opposite to the angles X,Y, Z, respectively, and 2s = x + y + z.
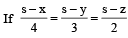 and area of incircle of the triangle
and area of incircle of the triangle 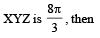


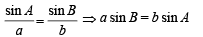
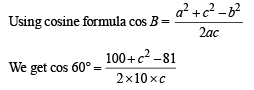
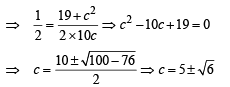
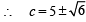 (both the values are less than 9 and 10),
(both the values are less than 9 and 10),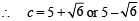 both are possible.
both are possible.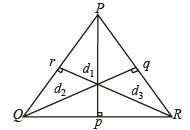
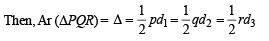

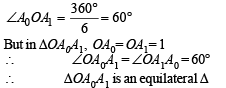
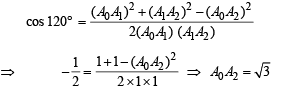
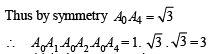
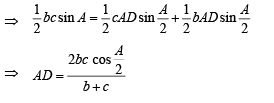
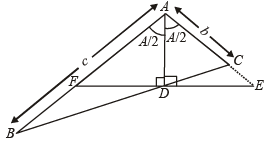

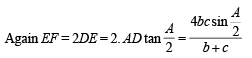
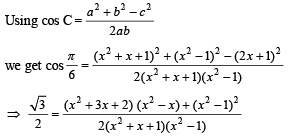
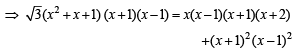
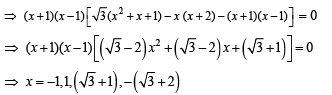
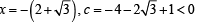 which is not possible
which is not possible