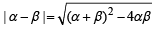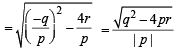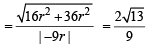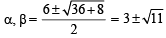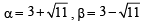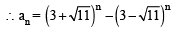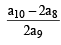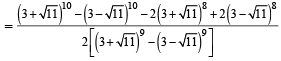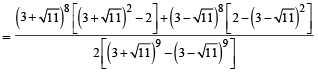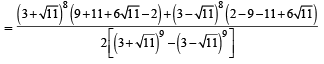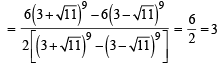Test: JEE Main 35 Year PYQs- Quadratic Equation & Inequalities (Inequalities) - JEE MCQ
30 Questions MCQ Test - Test: JEE Main 35 Year PYQs- Quadratic Equation & Inequalities (Inequalities)
If α ≠ β but α2 = 5α – 3 and β2 = 5β – 3 then the equation having α/β and β/α as its roots is [2002]
Difference between the corresponding roots of x2+ax+b=0 and x2+bx+a=0 is same and a ≠ b, then [2002]
| 1 Crore+ students have signed up on EduRev. Have you? Download the App |
Product of real roots of the equation t2x2+|x|+9=0 [2002]
If p and q are the roots of the equation x2+px+q=0, then
If a, b, c are distinct +ve real numbers and a2+b2+c2=1 then ab + bc + ca is [2002]
If the sum of the roots of the quadratic equation 2ax2 + bx +c= 0 is equal to the sum of the squares of their reciprocals, then 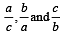 are in [2003]
are in [2003]
The value of ' a' for which one root of the quadratic equation (a2 -5a + 3) x2 +(3a - 1)x + 2= 0 is twice as large as the other is [2003]
The number of real roots of the equation x2 - 3|x| + 2 = 0 is
The real number x when added to its inverse gives the minimum value of the sum at x equal to [2003]
Let two numbers have arith metic mean 9 and geometric mean 4. Then these numbers are the roots of the quadratic equation[2004]
If (1- p) is a root of quadratic equation x2 + px + (1 -p)=0 th en its r oot are [2004]
If one r oot of th e equation x2 + px + 12=0 is 4, wh ile the equation x2 + px +q= 0 has equal r oots , then th e value of ‘q’ is[2004]
In a triangle PQR, 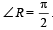 . If tan
. If tan 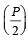 and – tan
and – tan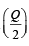 are the roots of ax2 + bx + c = 0, a ≠ 0 then [2005]
are the roots of ax2 + bx + c = 0, a ≠ 0 then [2005]
If both the roots of the quadratic equation x2 - 2kx + k2 + k – 5 = 0 are less than 5, then k lies in the interval [2005]
If the roots of the quadratic equation x2 + px +q= 0 are tan30° and tan15°, respectively, then the value of 2 + q – p is [2006]
All the values of m for which both roots of the equation x2 - 2mx +m2 - 1=0 are greater than – 2 but less then 4, lie in the interval [2006]
If x is real, the maximum value of 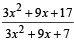 is [2006]
is [2006]
If the difference between the roots of the equation x2 + ax + 1 = 0 is less than 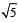 , then the set of possible values of a is [2007]
, then the set of possible values of a is [2007]
The locus of any complex number which satisfies 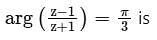
The quadritic equations x2 – 6x + a = 0 and x2 – cx + 6 = 0 have one root in common. The other roots of the first and second equations are integers in the ratio 4 : 3. Then the common root is [2009]
If the roots of the equation bx2 + cx + a = 0 be imaginary, then for all real values of x, the expression 3b2x2 + 6bcx + 2c2 is : [2009]
If 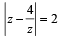 then the maximum value of | Z | is equal to : [2009]
then the maximum value of | Z | is equal to : [2009]
If α and β are the roots of the equation x2 – x + 1 = 0, then α2009 + β2009 = [2010]
The equation esinx – e–sinx– 4 = 0 has : [2012]
The real number k for which the equation, 2x3 + 3x + k = 0 has two distinct real roots in [0, 1] [JEE M 2013]
The number of values of k , for which the system of equations : [JEE M 2013]
(k + 1) x + 8y = 4k
kx + (k + 3) y = 3k – 1
has no solution, is
If the equations x2 + 2x + 3 = 0 and ax2 + bx + c = 0, a,b,c ∈ R, have a common root, then a : b : c is [JEE M 2013]
If a ∈ R and the equation -3 ( x - [ x])2 + 2 ( x- [ x])+a 2 =0 (where [x] denotes the greatest integer ≤ x ) has no integral solution, then all possible values of a lie in the interval: [JEE M 2014]
Let α and β be the roots of equation px2 + qx +r= 0, p ≠ 0. If p, q, r are in A.P. and 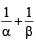 = 4 then the value of |α -β| is: [JEE M 2014]
= 4 then the value of |α -β| is: [JEE M 2014]
Let α and β be the roots of equation x2 – 6x – 2 = 0. If an = αn – βn, for n ≥ 1, then the value 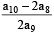 is equal to :[JEE M 2015]
is equal to :[JEE M 2015]


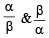 as its roots is
as its roots is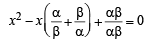
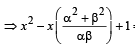 = 0 or 3x2 – 19x +3 = 0
= 0 or 3x2 – 19x +3 = 0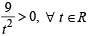

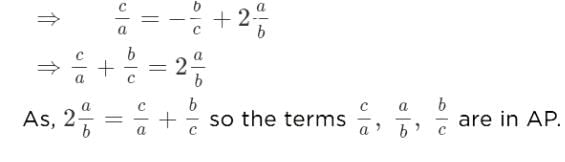
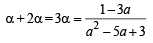
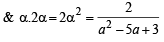
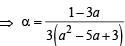
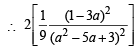
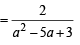
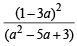 =
= 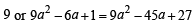
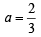
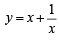 or
or 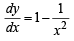
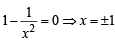
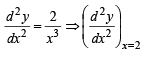 = 2(+ve minima) ∴x = 1
= 2(+ve minima) ∴x = 1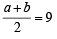 and
and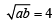
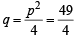
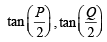 are the roots of ax2 + bx +c= 0
are the roots of ax2 + bx +c= 0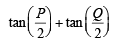
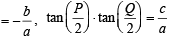
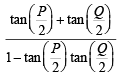
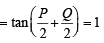
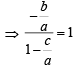
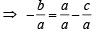
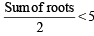
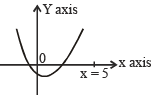
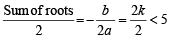
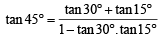
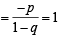
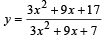
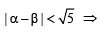
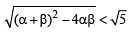
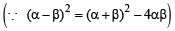
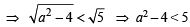
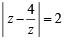
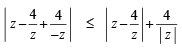
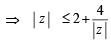
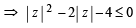
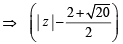
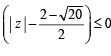
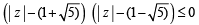
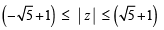
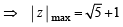
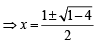
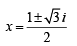
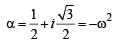
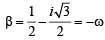
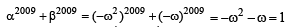
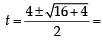
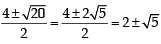
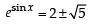 ( ∵ t=esinx)
( ∵ t=esinx)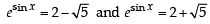
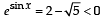 and
and 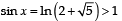
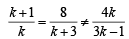 (∵ System has no solution)
(∵ System has no solution)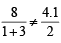 which is false
which is false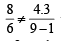 which is true, therefore k = 3
which is true, therefore k = 3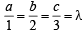 (say)
(say) 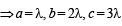
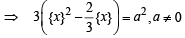
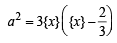
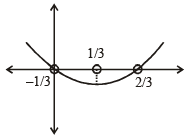
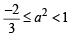 (by graph)
(by graph)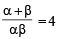
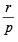
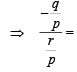 4 ⇒ q = -4r ....(ii)
4 ⇒ q = -4r ....(ii)