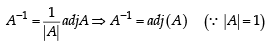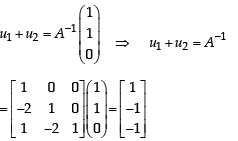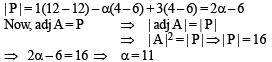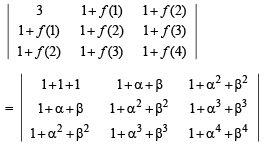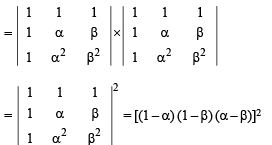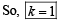Test: JEE Main 35 Year PYQs- Matrices and Determinants - JEE MCQ
30 Questions MCQ Test - Test: JEE Main 35 Year PYQs- Matrices and Determinants
If a > 0 and discriminant of ax2+2bx+c is –ve, then


If the system of linear equations
x + 2ay +az = 0 ; x +3by+bz = 0 ; x +4cy+cz = 0 ; has a non - zero solution, then a, b, c.
If 1, ω,ω2 are the cube roots of unity, then
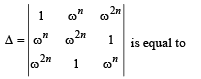
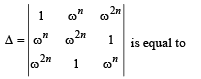
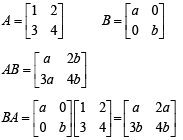
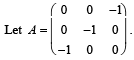 The only correct statement about the matrix A is
The only correct statement about the matrix A is
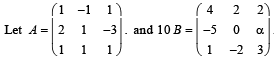 If B is the inverseof matrix A, then α is
If B is the inverseof matrix A, then α is
If a1, a2 , a3, ......,an, .... are in G.P., then the value of the determinant
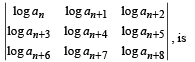
If A2 – A +I=0 , then the inverse of A is
The system of equations
α x + y + z = α – 1
x + α y + z = α – 1
x + y + α z = α – 1
has infinite solutions, if α is
If a2 + b2 + c2 = – 2 and
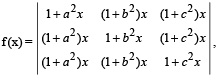
then f (x) is a polynomial of degree
If a1 , a2,a3 , ............, an , ...... are in G. P., then the determinant
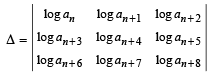
is equal to
If A and B are square matrices of size n × n such that A2 - B2 = (A -B)(A+B), then which of the following will be always true?
Let A be a 2 × 2 matrix with real entries. Let I be the 2 × 2 identity matrix. Denote by tr(A), the sum of diagonal entries of a. Assume that A2 = I.
Statement-1 : If A ≠ I and A ≠ –I, then det(A) = –1
Statement-2 : If A ≠ I and A ≠ –I, then tr (A) ≠ 0.
Let a, b, c be any real numbers. Suppose that there are real numbers x, y, z not all zero such that x = cy + bz, y = az + cx, and z = bx + ay. Then a2 + b2 + c2 + 2abc is equal to
Let A be a square matrix all of whose entries are integers. Then which one of the following is true?
Let A be a 2 × 2 matrix
Statement -1 : adj (adj A) = A
Statement -2 : |adj A |= |A|
Let a, b, c be such that b(a + c) ≠ 0 if
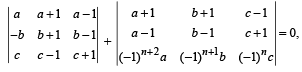
then the value of n is :
The number of 3 × 3 non-singular matrices, with four entries as 1 and all other entries as 0, is
Let A be a 2 × 2 matrix with non-zero entries and let A2 = I , where I is 2 × 2 identity matrix. Define Tr(A) = sum of diagonal elements of A and |A| = determinant of matrix A.
Statement - 1 : Tr(A) = 0.
Statement -2 : |A| = 1.
Consider the system of linear equations ;
x1 + 2x2 + x3 = 3
2x1 + 3x2 + x3 = 3
3x1 + 5x2 + 2x3 = 1
The system has
The number of values of k for which the linear equations 4x + ky + 2z = 0 , kx + 4y + z = 0 and 2x + 2y + z = 0 possess a non-zero solution is
Let A and B be two symmetric matrices of order 3.
Statement-1: A(BA) and (AB)A are symmetric matrices.
Statement-2: AB is symmetric matrix if matrix multiplication of A with B is commutative.
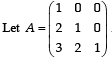 If u1 and u2 are column matrices such that
If u1 and u2 are column matrices such that 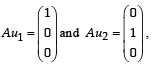 then u1 + u2 is equal to :
then u1 + u2 is equal to :
Let P and Q be 3 x 3 matrices P ≠ Q. If P3 = Q3 and P2Q = Q2P then determinant of (P2 + Q2) is equal to :
If 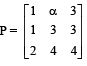 is the adjoint of a 3 × 3 matrix A and |A| = 4, then α is equal to :
is the adjoint of a 3 × 3 matrix A and |A| = 4, then α is equal to :
If α, β ≠ 0, and f (n) = αn +βn and
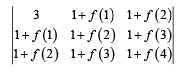
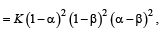 then K is equal to:
then K is equal to:
If A is a 3 × 3 non-singular matrix such that AA' = A'A and B = A–1A', then BB' equals:


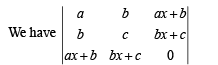
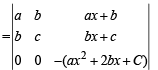
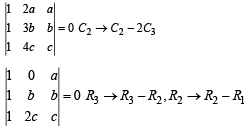
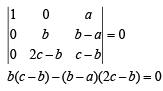
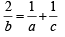

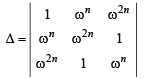
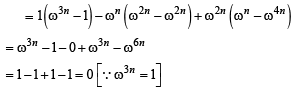
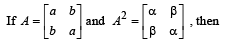

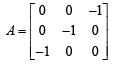
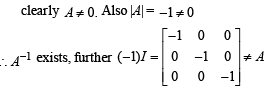
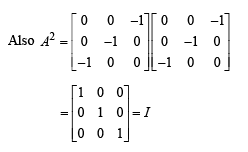
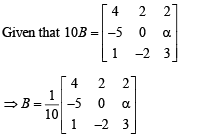
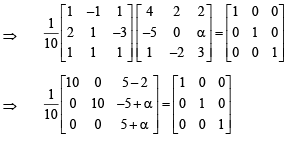
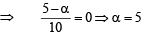
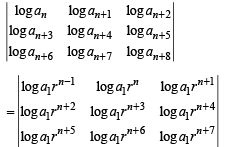
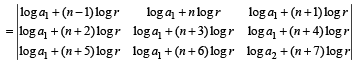
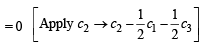
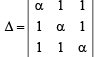
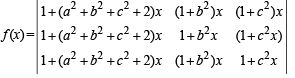

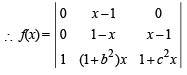
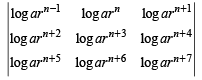
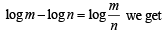
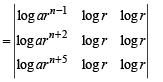
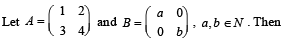

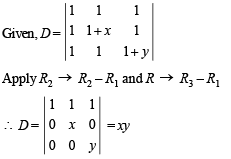
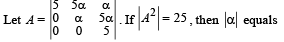
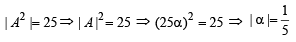
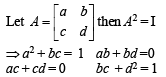
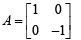
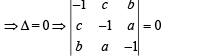

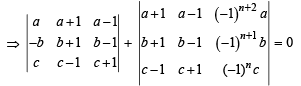

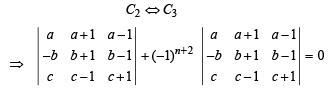
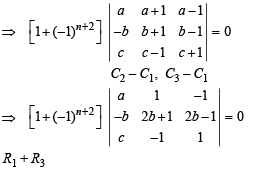
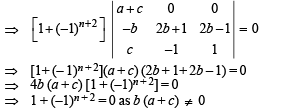
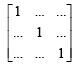 are 6 non-singular matrices because 6 blanks will be filled by 5 zeros and 1 one.
are 6 non-singular matrices because 6 blanks will be filled by 5 zeros and 1 one.  are 6 non-singular matrices.
are 6 non-singular matrices.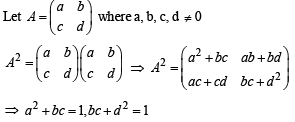
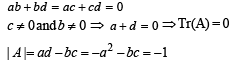
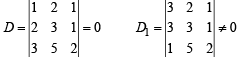
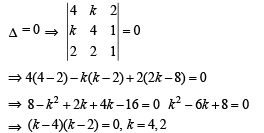
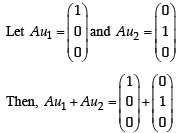
 ..(1)
..(1)