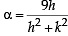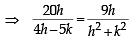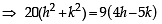Test: Single Correct MCQs: Circle | JEE Advanced - JEE MCQ
24 Questions MCQ Test - Test: Single Correct MCQs: Circle | JEE Advanced
A square is inscribed in the circle x2 + y2 – 2x + 4y + 3 = 0. Its sides are parallel to the coordinate axes. The one vertex of the square is (1980)
Two circles x2 + y2 = 6 and x2 + y2 – 6x + 8 = 0 are given. Then the equation of the circle through their points of intersection and the point (1, 1) is (1980)
| 1 Crore+ students have signed up on EduRev. Have you? Download the App |
The centre of the circle passing through the point (0, 1) and touching the curve y = x2 at (2, 4) is (1983 - 1 Mark)
The equation of the circle passing through (1, 1) and the points of intersection of x2 + y2 + 13x – 3y = 0 and 2x2 + 2y2 + 4x – 7y – 25 = 0 is (1983 - 1 Mark)
The locus of the mid -point of a chord of the circle x2 + y2 = 4 which subtends a right angle at the origin is (1984 - 2 Marks)
If a circle passes through the point (a, b) and cuts the circle x2 + y2 = k2 orthogonally, then the equation of the locus of its centre is (1988 - 2 Marks)
If the two circles (x – 1)2 + (y – 3)2 = r2 and x2 + y2 – 8x + 2y + 8 = 0 intersect in two distinct points, then (1989 - 2 Marks)
The lines 2x – 3y = 5 and 3x – 4y = 7 are diameters of a circle of area 154 sq. units. Then the equation of this circle is
The centre of a circle passing through the points (0, 0), (1, 0) and touching the circle x2 + y2 = 9 is (1992 - 2 Marks)
The locus of the centre of a circle, which touches externally the circle x2 + y2 – 6x – 6y + 14 = 0 and also touches the y-axis, is given by the equation: (1993 - 1 Marks)
The circles x2 + y2 – 10x + 16 = 0 and x2 + y2 = r2 intersect each other in two distinct points if (1994)
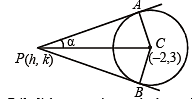
The angle between a pair of tangents drawn from a point P to the circle x2 + y2 + 4x – 6y + 9 sin2α + 13 cos2α = 0 is 2α.The equation of the locus of the point P is (1996 - 1 Mark)
If two distinct chords, drawn from the point (p, q) on the circle x2 + y2 = px + qy (where pq ≠ 0) are bisected by the x –axis, then (1999 - 2 Marks)
The triangle PQR is inscribed in the circle x2 + y2 = 25. If Q and R have co-ordinates (3,4) and (–4, 3) respectively, then ∠QPR is equal to (2000S)
If the circles x2 + y2 + 2x + 2ky + 6 = 0, x2 + y2 + 2ky + k = 0 intersect orthogonally, then k is (2000S)
Let AB be a chord of the circle x2 + y2 = r2 subtending a right angle at the centre. Then the locus of the centroid of the triangle PAB as P moves on the circle is (2001S)
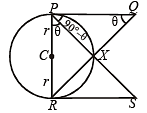
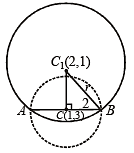
Let PQ and RS be tangents at the extremities of the diameter PR of a circle of radius r. If PS and RQ intersect at a point X on the circumference of the circle, then 2r equals (2001S)
If the tangent at the point P on the circle x2 + y2 + 6x + 6y = 2 meets a straight line 5x –2y + 6 = 0 at a point Q on the y - axis, then the length of PQ is (2002S)
The centre of circle inscribed in square formed by the lines x2 – 8x + 12 = 0 and y2 – 14y + 45 = 0, is (2003S)
If one of the diameters of the circle x2 + y2 – 2x – 6y + 6 = 0 is a chord to the circle with centre (2, 1), then the radius of the circle is (2004S)
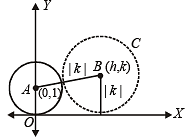
A circle is given by x2 + (y–1)2 = 1, another circle C touches it externally and also the x-axis, then the locus of its centre is (2005S)
Tangents drawn from the point P(1, 8) to the circle x2 + y2 –6x– 4y –11 = 0 touch the circle at the points A and B. The equation of the circumcircle of the triangle PAB is (2009)
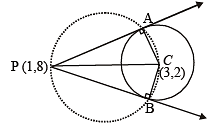
The circle passing through the point (– 1, 0) and touching the y-axis at (0, 2) also passes through the point. (2011)
The locus of th e mid-point of the ch or d of con tact of tangents drawn from points lying on the straight line 4x – 5y = 20 to the circle x2 + y2 = 9 is (2012)


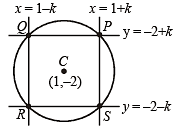
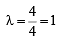
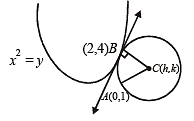
 i.e., 4x – y = 4
i.e., 4x – y = 4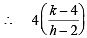 = -1 ⇒ 4k = 18… (1)
= -1 ⇒ 4k = 18… (1) 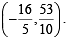
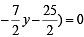
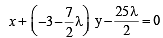

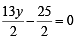
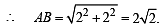
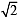
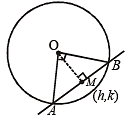
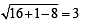
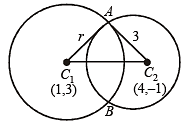
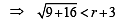 and 5 > |r – 3 |
and 5 > |r – 3 |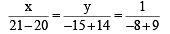
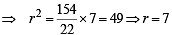

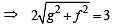
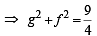


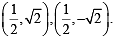
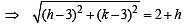

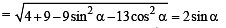
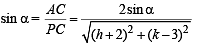

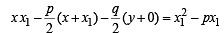 (using T = S1)
(using T = S1)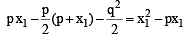
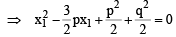
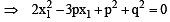
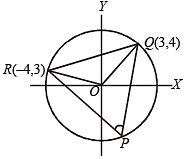
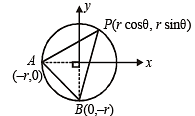
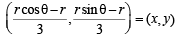
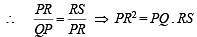
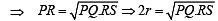

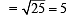
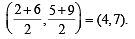


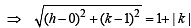

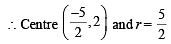


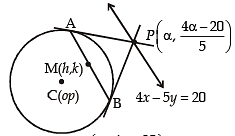
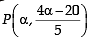
 ....(1)
....(1)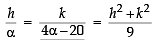
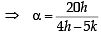 and
and