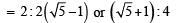Test: MCQs (One or More Correct Option): Conic Sections | JEE Advanced - JEE MCQ
18 Questions MCQ Test - Test: MCQs (One or More Correct Option): Conic Sections | JEE Advanced
The n umber of values of c such that the straight line y = 4x + c touches the curve (x2/4) + y2 = 1 is (1998 - 2 Marks)
If P = (x, y), F1 = (3, 0), F2 = (–3, 0) and 16x2 + 25y2 = 400, then PF1 +PF2 equals (1998 - 2 Marks)
| 1 Crore+ students have signed up on EduRev. Have you? Download the App |
On the ellipse 4 x2 + 9y2 =1 , the points at which the tangents are parallel to the line 8x = 9y are(1999 - 3 Marks)
The equations of th e common tangents to the parabola y = x2 and y = – (x – 2)2 is/are (2006 - 5M, –1)
Let a hyperbola passes through the focus of the ellipse 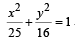 . The transverse and conjugate axes of this hyperbola coincide with the major and minor axes of the given ellipse, also the product of eccentricities of given ellipse and hyperbola is 1, then (2006 - 5M, –1)
. The transverse and conjugate axes of this hyperbola coincide with the major and minor axes of the given ellipse, also the product of eccentricities of given ellipse and hyperbola is 1, then (2006 - 5M, –1)
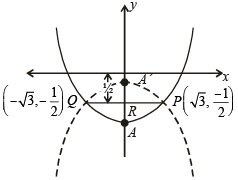
Let P(x1, y1) and Q(x2, y2), y1 < 0, y2 < 0, be the end points of the latus rectum of the ellipse x2 + 4y2 = 4. The equations of parabolas with latus rectum PQ are (2008)
In a triangle ABC with fixed base BC, the vertex A moves such that
cosB + cosC = 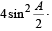 .
.
If a, b and c denote the lengths of the sides of the triangle opposite to the angles A, B and C, respectively, then
The tangent PT and the normal PN to the parabola y2 = 4ax at a point P on it meet its axis at points T and N, respectively.The locus of the centroid of the triangle PTN is a parabola whose(2009)
An ellipse intersects the hyperbola 2x2 – 2y2 = 1 orthogonally.The eccentricity of the ellipse is reciprocal of that of the hyperbola. If the axes of the ellipse are along the coordinate axes, then (2009)
Let A and B be two distinct points on the parabola y2 = 4x. If the axis of the parabola touches a circle of radius r having AB as its diameter, then the slope of the line joining A and B can be
(2010)
Let the eccentricity of the hyperbol a  abbereciprocal to that of the ellipse x2 + 4y2 = 4. If the hyperbola passes through a focus of the ellipse, then (2011)
abbereciprocal to that of the ellipse x2 + 4y2 = 4. If the hyperbola passes through a focus of the ellipse, then (2011)
Let L be a normal to the parabola y2 = 4x. If L passes through the point (9, 6), then L is given by (2011)
Tangents are drawn to the hyperbola 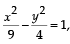 parallel to the straight line 2x – y = 1. The points of contact of the tangents on the hyperbola are (2012)
parallel to the straight line 2x – y = 1. The points of contact of the tangents on the hyperbola are (2012)
Let P and Q be distinct points on the parabola y2 = 2x such that a circle with PQ as diameter passes through the vertex O of the parabola. If P lies in the first quadrant and the area of the triangle ΔOPQ is 3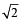 , then which of the following is (are) the coordinates of P? (JEE Adv. 2015)
, then which of the following is (are) the coordinates of P? (JEE Adv. 2015)
Let E1 and E2 be two ellipses whose centers are at the origin.
The major axes of E1 and E2 lie along the x-axis and the y-axis, respectively. Let S be the circle x2 + (y – 1)2 = 2. The straight line x + y = 3 touches the curves S, E1 and E2 at P, Q and R respectively. Suppose that PQ = PR = 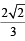
If e1 and e2 are the eccentricities of E1 and E2, respectively, then the correct expression(s) is (are) (JEE Adv. 2015)
Consider the hyperbola H : x2 – y2 = 1 and a circle S with center N(x2, 0). Suppose that H and S touch each other at a point P(x1, y1) with x1 > 1 and y1 > 0. The common tangent to H and S at P intersects the x-axis at point M. If (l, m) is the centroid of the triangle PMN, then the correct expression(s) is(are) (JEE Adv. 2015)
The circle C1 : x2 + y2 = 3, with centre at O, intersects the parabola x2 = 2y at the point P in the first quadrant. Let the tangent to the circle C1, at P touches other two circles C2 and C3 at R2 and R3, respectively. Suppose C2 and C3 have equal radii 2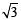 and centres Q2 and Q3, respectively. If Q2 and Q3 lie on the y–axis, then (JEE Adv. 2016)
and centres Q2 and Q3, respectively. If Q2 and Q3 lie on the y–axis, then (JEE Adv. 2016)
Let P be the point on the parabola y2 = 4x wh ich is at the shortest distance from the center S of the circle x2 + y2 – 4x –16y + 64 = 0. Let Q be the point on the circle dividing the line segment SP internally. Then (JEE Adv. 2016)


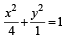 (an ellipse) and given line is y = 4x + c.
(an ellipse) and given line is y = 4x + c.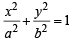
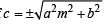
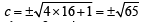
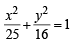
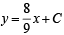 be the tangent to
be the tangent to 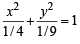
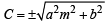
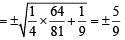
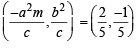
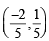
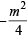
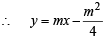 is tangent to y = x2
is tangent to y = x2 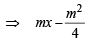 = x2 + 4x – 4
= x2 + 4x – 4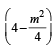 = 0
= 0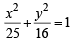
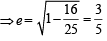
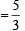
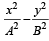 = 1 then
= 1 then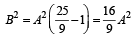
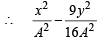 = 1
= 1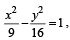 focus of hyperbola is (5, 0), vertex of hyperbola is (3, 0).
focus of hyperbola is (5, 0), vertex of hyperbola is (3, 0).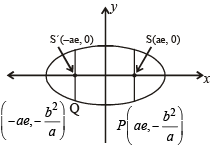
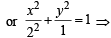 a = 2, b = 1
a = 2, b = 1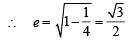
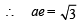
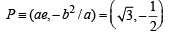
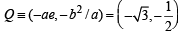
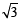
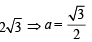
 ∴ Coordinates of A =
∴ Coordinates of A = 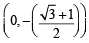
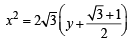 or
or 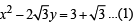
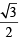
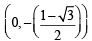
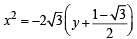 or
or 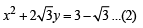
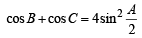
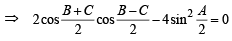
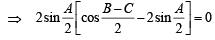

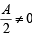
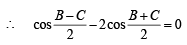
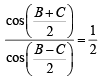
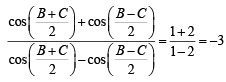
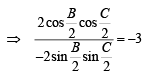
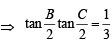
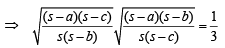
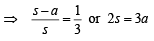
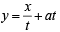
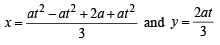
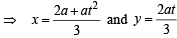
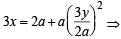
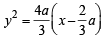
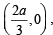 directrix as
directrix as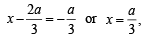 latus r ectum as
latus r ectum as 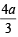 and
and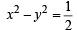 ...(1)
...(1)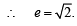
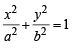
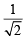
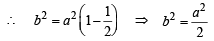

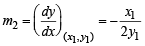
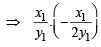
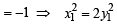
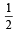
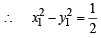 ...(ii)
...(ii)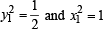
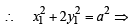 1 + 1 = a2 or a2 =2
1 + 1 = a2 or a2 =2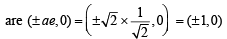
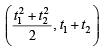
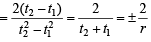
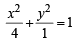
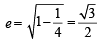
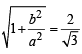
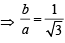
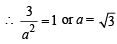
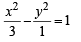
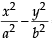 = are
= are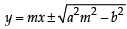 with the points of contact
with the points of contact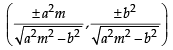
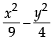 = is parallel to 2x – y = 1, therefore slope of tangent = 2
= is parallel to 2x – y = 1, therefore slope of tangent = 2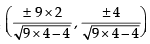
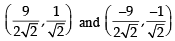
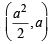 Let Q be the point
Let Q be the point 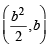 Clearly a > 0.
Clearly a > 0.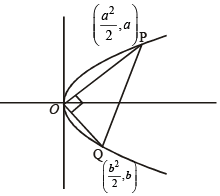
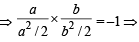 = –1 ⇒ ab = –4
= –1 ⇒ ab = –4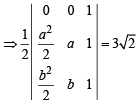
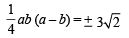
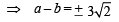 (using ab = –4)
(using ab = –4)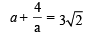 (using ab = –4)
(using ab = –4)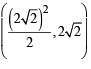 or
or 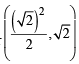
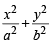 = 1 where a > b
= 1 where a > b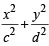 = 1 where c < d
= 1 where c < d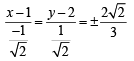
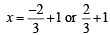 and
and 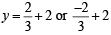
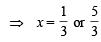 and
and 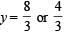
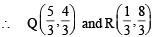
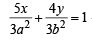 which is identical to
which is identical to 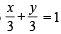
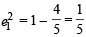
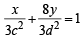 identical to
identical to 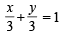
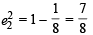
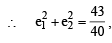
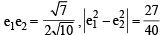
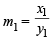
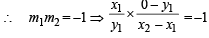
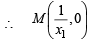
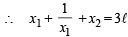 and y1 = 3m
and y1 = 3m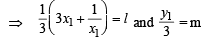
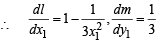
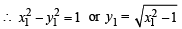
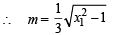

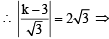 k = 9 or –3
k = 9 or –3
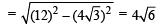
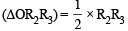 × length of ⊥ from originto tangent
× length of ⊥ from originto tangent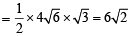
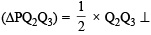 distance of P from
distance of P from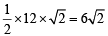
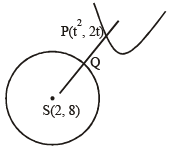
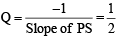
 and SQ = r = 2
and SQ = r = 2