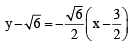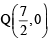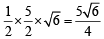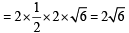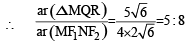Test: Comprehension Based Questions: Conic Sections - JEE MCQ
14 Questions MCQ Test - Test: Comprehension Based Questions: Conic Sections
PASSAGE 1
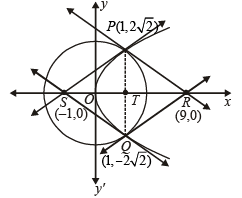
Consider the circle x2 + y2 = 9 and the parabola y2 = 8x. They intersect at P and Q in the first and the fourth quadrants, respectively. Tangents to the curcle at P and Q intersect the x-axis at R and tangents to the parabola at P and Q intersect the x-axis at S. (2007 -4 marks)
Q. The ratio of the areas of the triangles PQS and PQR is
PASSAGE 1
Consider the circle x2 + y2 = 9 and the parabola y2 = 8x. They intersect at P and Q in the first and the fourth quadrants, respectively. Tangents to the curcle at P and Q intersect the x-axis at R and tangents to the parabola at P and Q intersect the x-axis at S. (2007 -4 marks)
Q. The radius of the circumcircle of the triangle PRS is (2007 -4 marks)
| 1 Crore+ students have signed up on EduRev. Have you? Download the App |
PASSAGE 1
Consider the circle x2 + y2 = 9 and the parabola y2 = 8x. They intersect at P and Q in the first and the fourth quadrants, respectively. Tangents to the curcle at P and Q intersect the x-axis at R and tangents to the parabola at P and Q intersect the x-axis at S. (2007 -4 marks)
Q. The radius of the incircle of the triangle PQR is (2007 -4 marks)
PASSAGE 2
The circle x2 + y2 – 8x = 0 and hyperbola 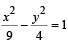 intersect atthe points A and B. (2010)
intersect atthe points A and B. (2010)
Q. Equation of a common tangent with positive slope to the circle as well as to the hyperbola is
PASSAGE 2
The circle x2 + y2 – 8x = 0 and hyperbola 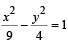 intersect atthe points A and B. (2010)
intersect atthe points A and B. (2010)
Q. Equation of the circle with AB as its diameter is
PASSAGE 3
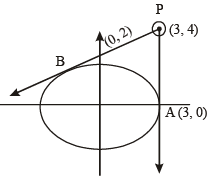
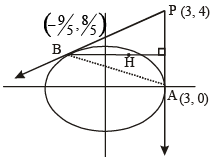
Tangents are drawn from the point P(3, 4) to the ellipse 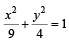 touching the ellipse at points A and B. (2010)
touching the ellipse at points A and B. (2010)
Q. The coordinates of A and B are
PASSAGE 3
Tangents are drawn from the point P(3, 4) to the ellipse 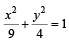 touching the ellipse at points A and B. (2010)
touching the ellipse at points A and B. (2010)
Q. The orthocenter of the triangle PAB is
PASSAGE 3
Tangents are drawn from the point P(3, 4) to the ellipse 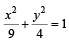 touching the ellipse at points A and B. (2010)
touching the ellipse at points A and B. (2010)
Q. The equation of the locus of the point whose distances from the point P and the line AB are equal, is
PASSAGE 4
Let PQ be a focal chord of the parabola y2 = 4ax. The tangents to the parabola at P and Q meet at a point lying on the line y = 2x + a, a > 0.
Q. Length of chord PQ is (JEE Adv. 2013)
PASSAGE 4
Let PQ be a focal chord of the parabola y2 = 4ax. The tangents to the parabola at P and Q meet at a point lying on the line y = 2x + a, a > 0.
Q. If chord PQ subtends an angle θ at the vertex of y2 = 4ax, then tan q = (JEE Adv. 2013)
PASSAGE 5
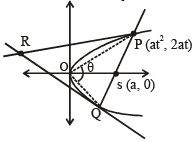
Let a, r, s, t be nonzero real numbers. Let P (at2, 2at), Q, R (ar2, 2ar) and S (as2, 2as) be distinct points on the parabola y2 = 4ax. Suppose that PQ is the focal chord and lines QR and PK are parallel, where K is the point (2a, 0) (JEE Adv. 2014)
Q. The value of r is
PASSAGE 5
Let a, r, s, t be nonzero real numbers. Let P (at2, 2at), Q, R (ar2, 2ar) and S (as2, 2as) be distinct points on the parabola y2 = 4ax. Suppose that PQ is the focal chord and lines QR and PK are parallel, where K is the point (2a, 0) (JEE Adv. 2014)
Q. If st = 1, then the tangent at P and the normal at S to the parabola meet at a point whose ordinate is
PASSAGE 6
Let F1(x1, 0) and F2(x2, 0) for x1 < 0 and x2 > 0, be the foci of the ellipse 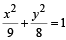 Suppose a parabola having vertex at the origin and focus at F2 intersects the ellipse at point M in the first quadrant and at point N in the fourth quadrant.
Suppose a parabola having vertex at the origin and focus at F2 intersects the ellipse at point M in the first quadrant and at point N in the fourth quadrant.
Q. The orthocentre of th e triangle F1MN is (JEE Adv. 2016)
PASSAGE 6
Let F1(x1, 0) and F2(x2, 0) for x1 < 0 and x2 > 0, be the foci of the ellipse 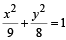 Suppose a parabola having vertex at the origin and focus at F2 intersects the ellipse at point M in the first quadrant and at point N in the fourth quadrant.
Suppose a parabola having vertex at the origin and focus at F2 intersects the ellipse at point M in the first quadrant and at point N in the fourth quadrant.
Q. If the tangen ts to the ellipse at M an d N meet at R and the normal to the parabola at M meets the x-axis at Q, then the ratio of area of the triangle MQR to area of the quadrilateral MF1NF2 is (JEE Adv. 2016)


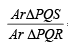
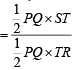
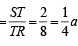
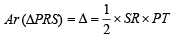
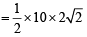
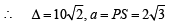
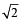 , c = SR = 10
, c = SR = 10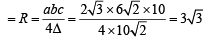
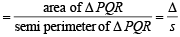
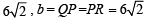
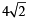
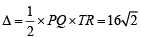
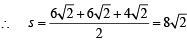
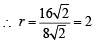
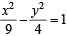 is
is 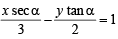
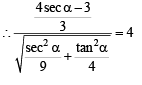
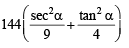
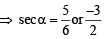
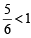 is not possible
is not possible
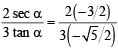 .
.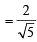
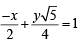
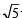 y + 4=0
y + 4=0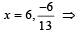
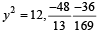 (not possible)
(not possible)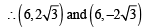 are points of intersection.
are points of intersection.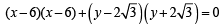
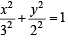 at the point (3 cosθ, 2 sinθ) is
at the point (3 cosθ, 2 sinθ) is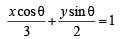
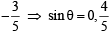
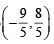
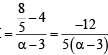
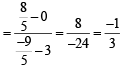
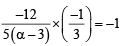
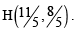
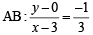 or x + 3y – 3=0
or x + 3y – 3=0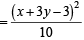
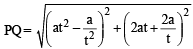
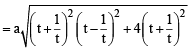
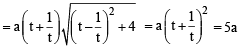

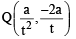
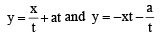
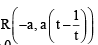
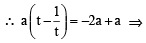
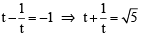
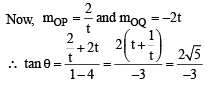
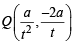
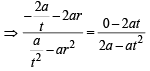
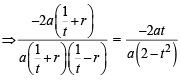
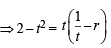
 otherwise Q will coincide with R]
otherwise Q will coincide with R]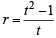
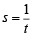
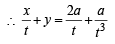
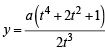
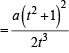
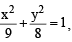

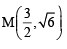 and
and 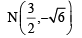
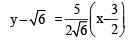
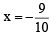
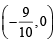
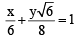 and
and 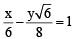
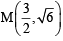 is
is