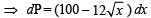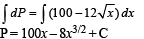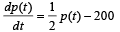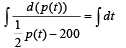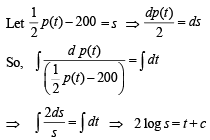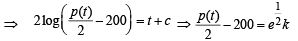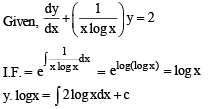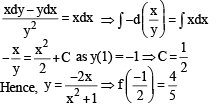Test: 35 Year JEE Previous Year Questions: Differential Equations - JEE MCQ
21 Questions MCQ Test - Test: 35 Year JEE Previous Year Questions: Differential Equations
Let a solution y = y(x) of the differential equation
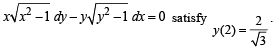
STATEMENT-1 : 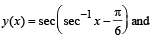
STATEMENT-2 : 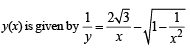
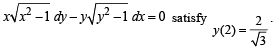
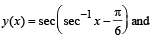
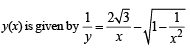
The order and degree of the differential equation 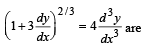
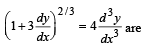
| 1 Crore+ students have signed up on EduRev. Have you? Download the App |
The solution of the equation 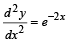
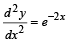
The degree and order of the differential equation of the family of all parabolas whose axis is x - axis, are respectively.
The solution of the differential equation 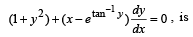
The differential equation for the family of circle x2 + y2 - 2ay = 0, where a is anarbitrary constant is
Solution of the differential equation ydx + (x + x2 y)dy = 0 is
The differential equation representing the family of curves 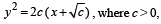 is a parameter, is of order and degree as follows :
is a parameter, is of order and degree as follows :
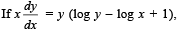 then the solution of theequation is
then the solution of theequation is
The differential equation whose solution is Ax2 + By2 = 1 where A and B are arbitrary constants is of
The differential equation of all circles passing through the origin and having their centres on the x-axis is
The soluton of the differential equation 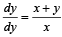 satisfying the condition y(1) =1 is
satisfying the condition y(1) =1 is
The differential equation which represents the family of curves 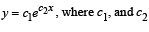 are arbitrary constants, is
are arbitrary constants, is
Solution of the differential equation
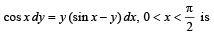
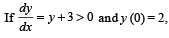 then y (ln 2) is equal to :
then y (ln 2) is equal to :
Let I be the purchase value of an equipment and V (t) be the value after it has been used for t years. The value V(t) depreciates at a rate given by differential equation 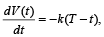 where k > 0 is a constant and T is thetotal life in years of the equipment. Then the scrap value V(T) of the equipment is
where k > 0 is a constant and T is thetotal life in years of the equipment. Then the scrap value V(T) of the equipment is
The population p (t) at time t of a certain mouse species satisfies the differential equation 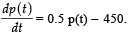 If p (0) = 850, then the time at which the population becomes zero is :
If p (0) = 850, then the time at which the population becomes zero is :
At present, a firm is manufacturing 2000 items. It is estimated that the rate of change of production P w.r.t. additional number of workers x is given by 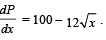 If thefirm employs 25 more workers, then the new level of production of items is
If thefirm employs 25 more workers, then the new level of production of items is
Let the population of rabbits surviving at time t be governed by the differential equation 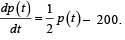 If p(0) = 100, then p(t) equals:
If p(0) = 100, then p(t) equals:
Let y(x) be the solution of the differential equation 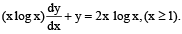 Then y (e) is equal to:
Then y (e) is equal to:
If a curve y = f(x) passes through the point (1, –1) and satisfies the differential equation, y(1 + xy) dx = x dy, then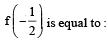


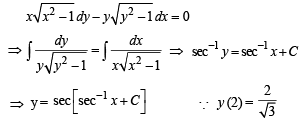

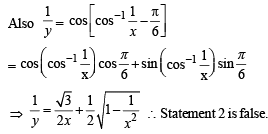
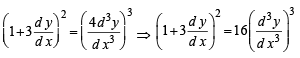
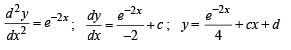
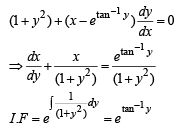
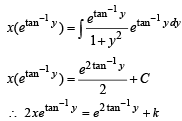
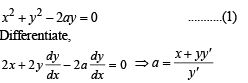
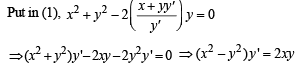
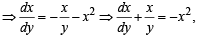
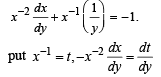
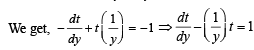
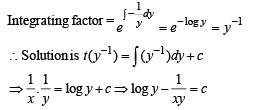
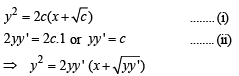
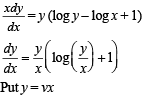
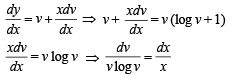
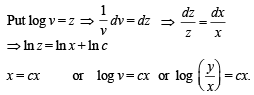
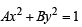 .........(1)
.........(1)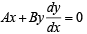 ..........(2)
..........(2)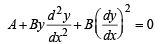 ........(3)
........(3)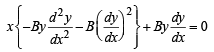

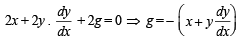
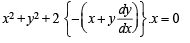
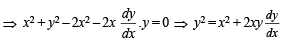
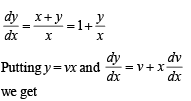
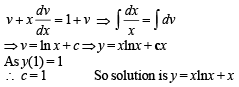
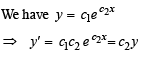
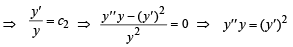
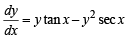
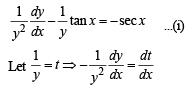
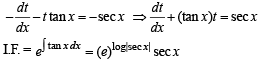
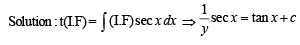
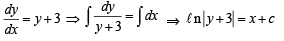
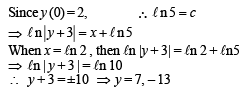

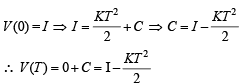
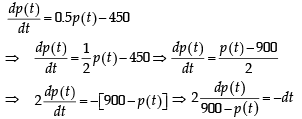
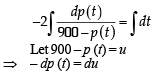

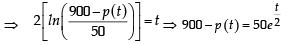
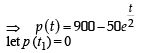
 ∴ t1 = 2ln 18
∴ t1 = 2ln 18