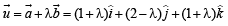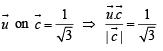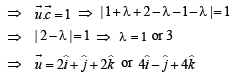JEE Advanced (Single Correct MCQs): Vector Algebra and Three Dimensional Geometry - JEE MCQ
30 Questions MCQ Test - JEE Advanced (Single Correct MCQs): Vector Algebra and Three Dimensional Geometry
The scalar 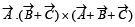 equals :
equals :
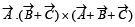 equals :
equals :For non-zero vectors 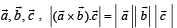 holds if and only if
holds if and only if
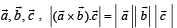 holds if and only if
holds if and only ifThe volume of the parallelopiped whose sides are given by 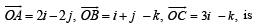
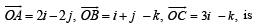
The points with position vectors 60i + 3j, 40 i – 8 j, ai – 52 j are collinear if
Let 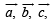 be three non - coplanar vectors and
be three non - coplanar vectors and 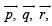 are vectors defined by the relations
are vectors defined by the relations 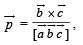
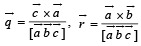 then the value of the expression
then the value of the expression 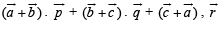 is equal to
is equal to
Let a, b, c be distinct non-negative numbers. If the vectors 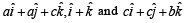 lie in a plane, then c is
lie in a plane, then c is
Let 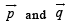 be the position vectors of P and Qr espectively, with respect to O and
be the position vectors of P and Qr espectively, with respect to O and 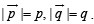 The points R and S divide PQ internally and externally in the ratio 2 : 3 respectively. If OR and OS are perpendicular then
The points R and S divide PQ internally and externally in the ratio 2 : 3 respectively. If OR and OS are perpendicular then
Let α, β, γ be distinct real numbers. The points with position vectors 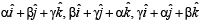
Let 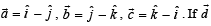 is a unit vector such that
is a unit vector such that 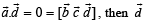 equals
equals
If 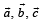 are non coplanar unit vectors such that
are non coplanar unit vectors such that 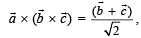 then the angle between
then the angle between 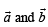 is
is
Let 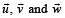 be vectors such that
be vectors such that 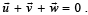 If
If 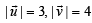 and
and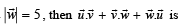
If 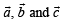 are three non coplanar vectors, then
are three non coplanar vectors, then 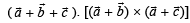 equals
equals
Let a = 2i + j – 2k and b = i + j. If c is a vector such that a. c = | c |, | c - a | = 2√2 and the angle between (a × b) and c is 30°, then | (a × b) × c| =
Let a =2i + j + k, b = i +2j –k and a unit vector c be coplanar. If c is perpendicular to a, then c =
If the vectors 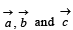 form the sides BC, CA and ABrespectively of a triangle ABC, then
form the sides BC, CA and ABrespectively of a triangle ABC, then
Let the vectors 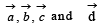 be such that
be such that  Let P1 and P2 be planes determined by the pairs of vectors
Let P1 and P2 be planes determined by the pairs of vectors 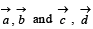 respectively. Thenthe angle between P1 and P2 is
respectively. Thenthe angle between P1 and P2 is
If 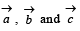 are unit coplanar vectors, then the scalar triple product
are unit coplanar vectors, then the scalar triple product 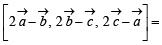
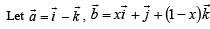 and
and 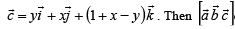 depends on
depends on
If 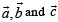 are unit vectors, then
are unit vectors, then 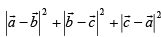 does NOT exceed
does NOT exceed
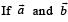 are two unit vectors such that
are two unit vectors such that 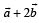 and
and 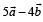 are perpendicular to each other then the angle between
are perpendicular to each other then the angle between 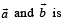
Let 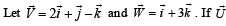 is a unit vector,, then the maximum value of the scalar triple product
is a unit vector,, then the maximum value of the scalar triple product 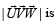
The value of k such that 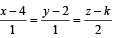 lies in the plane 2x – 4y + z = 7, is
lies in the plane 2x – 4y + z = 7, is
The value of ‘a’ so that the volume of parallelopiped formed by 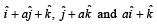 becomes minimum is
becomes minimum is
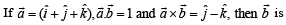
If the lines
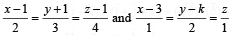 intersect, then the value of k is
intersect, then the value of k is
The unit vector which is orthogonal to the vector 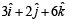 an d is coplanar with the vectors
an d is coplanar with the vectors 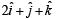 and
and 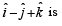
A variable plane at a distance of the one unit from the origin cuts the coordinates axes at A, B and C. If the centroid D (x, y, z) of triangle ABC satisfies the relation 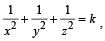 , then the value k is
, then the value k is
If 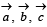 are three non-zero, non-coplanar vectors and
are three non-zero, non-coplanar vectors and
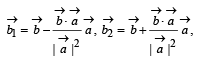
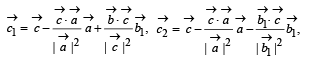
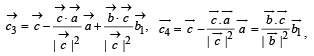
then the set of orthogonal vectors is
A plane which is perpendicular to two planes 2x – 2y + z = 0 and x – y + 2z = 4, passes through (1, –2, 1). The distance of the plane from the point (1, 2, 2) is
L et 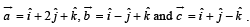 A vector in the plane of
A vector in the plane of 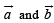 whose projection on
whose projection on 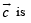
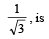


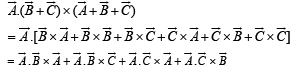
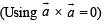
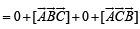
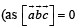 if any two vector are equal out of
if any two vector are equal out of 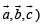
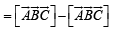
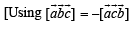
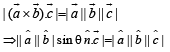
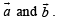
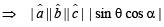
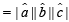 where θ is angle between
where θ is angle between 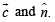
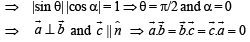

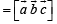
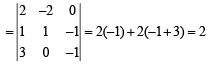
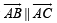
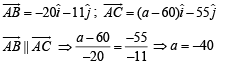
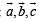 are non coplanar
are non coplanar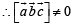
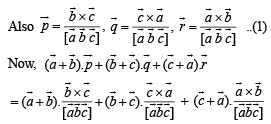
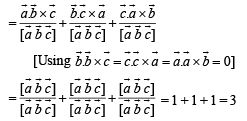
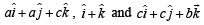 are coplanar.
are coplanar.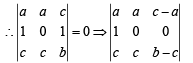
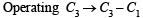
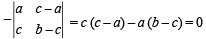
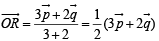
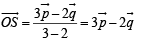

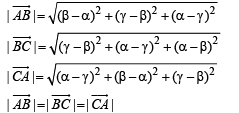
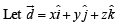
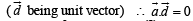
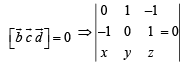
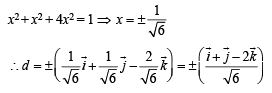
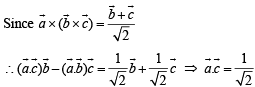
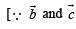 are non-coplanar]
are non-coplanar]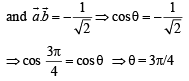
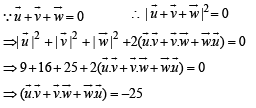
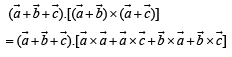
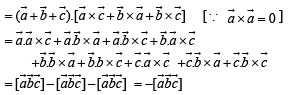
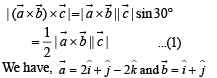
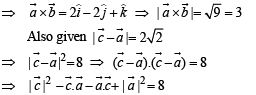
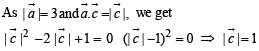
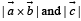 in (1), we get
in (1), we get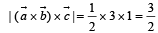
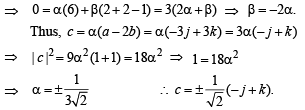
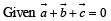 (by triangle law)
(by triangle law)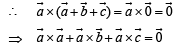
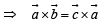
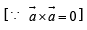
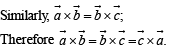
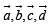 are vectors such that
are vectors such that 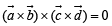
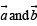
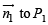 will be given by
will be given by 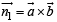
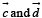
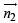 to P2 will be given by
to P2 will be given by 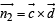
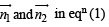
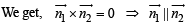
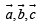 are unit coplanar vectors,
are unit coplanar vectors, 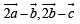 and
and 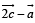 a re a lso coplan a r vector s. bein g lin ea r combination of
a re a lso coplan a r vector s. bein g lin ea r combination of 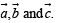
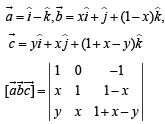
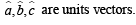
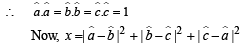
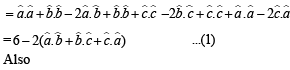
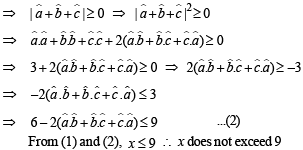
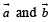 are two unit vectors
are two unit vectors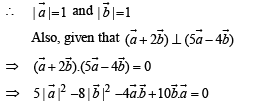
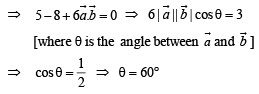
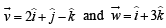 and u is a unit vector
and u is a unit vector 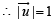
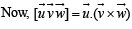
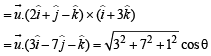
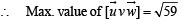
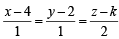 lies in th e plan e 2x - 4 y +z= 7, the point (4, 2, k) through which line passes must also lie on the given plane and hence 2 × 4 – 4 × 2 + k = 7 ⇒ k = 7
lies in th e plan e 2x - 4 y +z= 7, the point (4, 2, k) through which line passes must also lie on the given plane and hence 2 × 4 – 4 × 2 + k = 7 ⇒ k = 7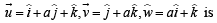
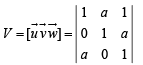
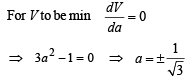
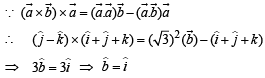
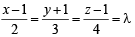
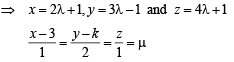
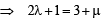 ...(1)
...(1)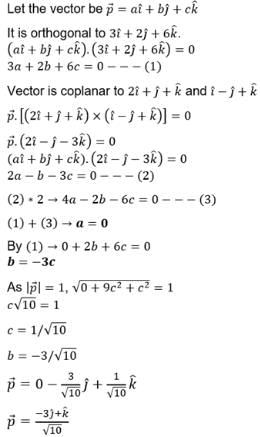
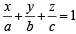 which meets the axes at A (a, 0, 0), B (0, b, 0) and C (0. 0, c).
which meets the axes at A (a, 0, 0), B (0, b, 0) and C (0. 0, c).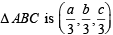
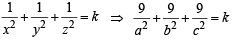
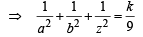 ...(1)
...(1)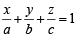 from (0, 0, 0) is 1 unit.
from (0, 0, 0) is 1 unit.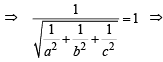

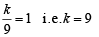
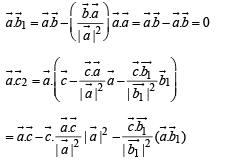
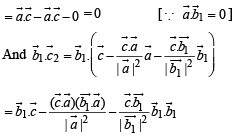
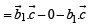
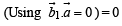
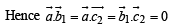
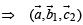 is a set of orthogonal vectors.
is a set of orthogonal vectors.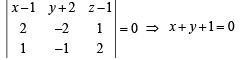
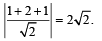
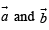 is
is