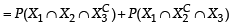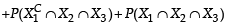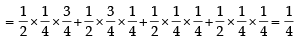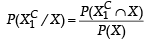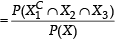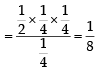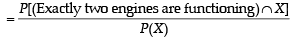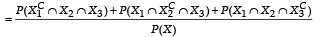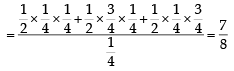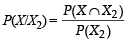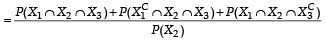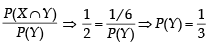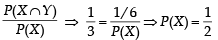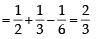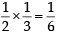Test: MCQs (One or More Correct Option): Probability | JEE Advanced - ENGAA MCQ
19 Questions MCQ Test - Test: MCQs (One or More Correct Option): Probability | JEE Advanced
If M and N are any two events, the probability that exactly one of them occurs is (1984 - 3 Marks)
A student appears for tests I, II and III. The student is successful if he passes either in tests I and II or tests I and III. The probabilities of the student passing in tests I, II and III are p, q and 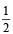 respectively. If the probability that the student is successful is
respectively. If the probability that the student is successful is 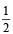 , then (1986 - 2 Marks)
, then (1986 - 2 Marks)
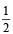 respectively. If the probability that the student is successful is
respectively. If the probability that the student is successful is 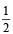 , then (1986 - 2 Marks)
, then (1986 - 2 Marks)The probability that at least one of the events A and B occurs is 0.6. If A and B occur simultaneously with probability 0.2, then 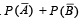 is (1987 - 2 Marks)
is (1987 - 2 Marks)
(Here 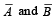 are complements of A and B, respectively).
are complements of A and B, respectively).
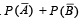 is (1987 - 2 Marks)
is (1987 - 2 Marks)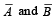 are complements of A and B, respectively).
are complements of A and B, respectively).For two given events A and B, P ( A ∩ B) (1988 - 2 Marks)
If E and F are independent events such that 0 < P(E) <1 and 0 < P(F) < 1, then (1989 - 2 Marks)
For any two events A and B in a sample space (1991 - 2 Marks)
E and F are two independent events. The probability that both E and F happen is 1/ 12 and the probability that neither E nor F happens is 1/2. Then, (1993 - 2 Marks)
Let 0 < P(A) < 1, 0 < P(B) < 1 and P ( A ∪ B) = P(A) + P(B) – P(A)P(B) then (1995S)
If from each of the three boxes containing 3 white and 1 black, 2 white and 2 black, 1 white and 3 black balls, one ball is drawn at random, then the probability that 2 white and 1 black ball will be drawn is (1998 - 2 Marks)
If 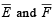 are the complementary events of events E and F respectively and if 0 < P(F) < 1, then (1998 - 2 Marks)
are the complementary events of events E and F respectively and if 0 < P(F) < 1, then (1998 - 2 Marks)
There are four machines and it is known that exactly two of them are faulty. They are tested, one by one, in a random order till both the faulty machines are identified. Then the probability that only two tests are needed is(1998 - 2 Marks)
If E and F are events with P(E) ≤ P(F) and P(E ∩ F) > 0, th en (1998 - 2 Marks)
A fair coin is tossed repeatedly. If the tail appears on first four tosses, then the probability of the head appearing on the fifth toss equals (1998 - 2 Marks)
Seven white balls and three black balls are randomly placed in a row. The probability that no two black balls are placed adjacently equals (1998 - 2 Marks)
The probabilities that a student passes in Mathematics, Physics and Chemistry are m, p and c, respectively. Of these subjects, the student has a 75% chance of passing in at least one, a 50% chance of passing in at least two, and a 40% chance of passing in exactly two. Which of the following relations are true? (1999 - 3 Marks)
Let E and F be two independent events. The probability that exactly one of them occurs is 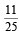 and the probability of none of them occurring is
and the probability of none of them occurring is 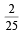 . If P(T) denotes the probability of occurrence of the event T, then (2011)
. If P(T) denotes the probability of occurrence of the event T, then (2011)
A ship is fitted with three engines E1 , E2 and E3 . The engines function independently of each other with respective probabilities 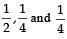 For the ship to be operational at least two of its engines must function. Let X denote the event that the ship is operational and let X1 , X2 and X3 denote respectively the events that the engines E1, E2 and E3 are functioning. Which of the following is(are) true ? (2012)
For the ship to be operational at least two of its engines must function. Let X denote the event that the ship is operational and let X1 , X2 and X3 denote respectively the events that the engines E1, E2 and E3 are functioning. Which of the following is(are) true ? (2012)
Let X and Y be two even ts such that 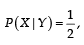
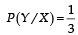 and
and 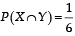 Which of the following is (are) correct ? (2012)
Which of the following is (are) correct ? (2012)
Four persons independently solve a certain problem correctly with probabilities 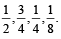 Then the probability that theproblem is solved correctly by at least one of them is (JEE Adv. 2013)
Then the probability that theproblem is solved correctly by at least one of them is (JEE Adv. 2013)


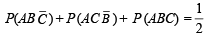
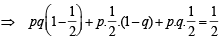
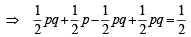

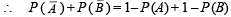
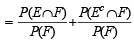
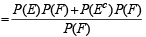
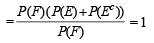
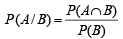
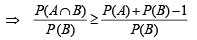
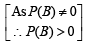
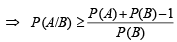 ∴ (a) is correct statement.
∴ (a) is correct statement.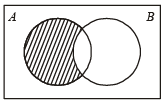
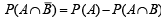
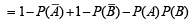
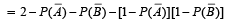
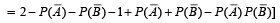
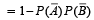 ∴ (c) is the correct statement.
∴ (c) is the correct statement.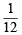
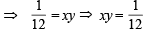 … (1)
… (1)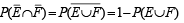
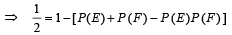
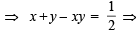
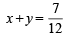 … (2)
… (2)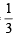 and y =
and y = 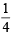 or x =
or x = 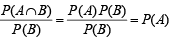
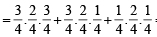
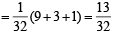
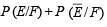
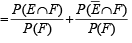
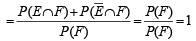
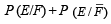
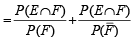
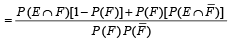
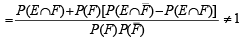
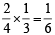
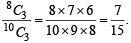
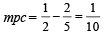
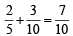
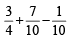
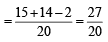
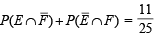
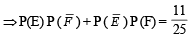
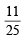
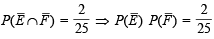
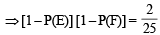
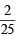 ...(3)
...(3)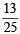 or P(E) P(F) =
or P(E) P(F) = 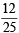 ...(4)
...(4)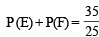 ...(5)
...(5)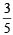 and P(F) =
and P(F) = 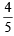 or P(E) =
or P(E) =