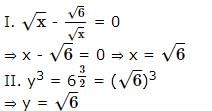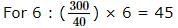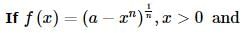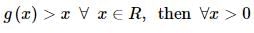CAT Practice Test - 30 - CAT MCQ
30 Questions MCQ Test - CAT Practice Test - 30
Ten yrs ago,the ages of the father and the son were in the ratio 6:1 and 10 yrs hence the ratio will become 2:1. The present age of the father is
The total number of integer pairs (x,y) satisfying the equation x + y = xy is :
In the following questions two equations numbered I and II are given. You have to solve both the equations and
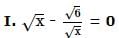

Let a, b, c, d be the lengths of consecutive sides of a rectangle. Which of the following can be the area of the rectangle?
Two identical circles intersect so that their centres and the points at which they intersect, form a square of side 1 cm. The area in sq. cm of the portion that is common to the two circles is
A boy appears for 5 papers, each of the same number of maximum marks. He scores in each of the papers in the ratio of 6 : 7 : 8 : 9 : 10. If his average score in all the five papers together was 60%, then in how many papers did he get more than 50% marks ?
ABCD is a rectangle. The points P and Q lie on AD and AB respectively. If the triangles PAQ, QBC and PCD all have the same areas and BQ = 2 then AQ = ?
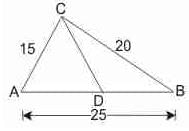
In the given figure, ACB is a right angled triangle. CD is the altitude. Circles are inscribed within the triangles ACD, BCD. P and Q are the centres of the circles. The distance PQ is :
x and y are real numbers satisfying the conditions 2 < x < 3 and –8 < y < –7. Which of the following expressions will have the least value?
Amar, Akbar and Anthony invested sums , a,b and c respectively under simple interest at the same rate of interest and for the same period . The amount with Akbar at the end of the period is equal to the interest earned by Amar during that period and the amount with Anthony at the end of the period is equal to the interest earned by Akbar during that period .Which of the following is the relation among a,b and c ?
Let f(x)= 6 - 12x + 9x2 - 2x3 , 1 ≤ x ≤ 4. Then the absolute maximum value of f(x) in the interval is
A mixture contains spirit and water is the ratio 3:2.If it contains 3 litres more spirit than water,the quantity of spirit in the mixture is
Let S be the set of integers x such that
I. 100 ≤ x ≤ 200
II. x is odd
III. x is divisible by 3 but not 7
How many elements does S contain?
Of 128 boxes of oranges, each box contains at least 120 and at most 144 oranges. The number of boxes containing the same number of oranges is at least
Last year Deepika saved 10 percent of his annual earnings. This year he earned 5 percent more than last year and he saved 12 percent of his annual earnings. The amount saved this year was what percent of the amount saved last year?
How many words can be formed by re-arranging the letters of the word ASCENT such that A and T occupy the first and last position respectively?
A man bets on number 16 on a roulette wheel 14 times and losses each time. On the 15th span he does a quick calculation and finds out that the number 12 had appeared twice in the 14 spans and is therefore, unable to decide whether to bet on 16 or 12 in the 15th span. Which will give him the best chance and what are the odds of winning on the bet that he takes? (Roulette has numbers 1 to 36)
A merchant buys two articles for Rs.600. He sells one of them at a profit of 22% and the other at a loss of 8% and makes no profit or loss in the end. What is the selling price of the article that he sold at a loss?
In a quadratic equation with leading coefficient 1, a student reads the coefficient 16 of x wrongly as 19 and obtain the roots as -15 and -4. The correct roots are
A race track is 1680 m long. In a race between A and B, A won by 30 seconds. In a race between A and C on the same track, A wins by 630 m. In a race between B and C on the same track, B wins by 96 seconds. The time taken by A to run the complete track is
There are blue vessels with volumes v1, v2, ...., vm, arranged in ascending order of volumn, v1 > 0.5 litre and vm < 1 litre. Each of these is full of water initially. The water from each these is emptied into a minimum number of empty white vessels, each having volumn 1 litre. The water from a blue vessel is not emptied into a white vessel unless the white vessel has enough empty volumn to hold all the water of the blue vessel. The number of white vessels required to empty all the blue vessels according to the above rules was n.
Q. Among the four values given below, which is the least upper bound on e, where e is the total empty volume in the white vessels at the n end of the above process ?
If Sn = 27 - 72 + 29 - 69 + 31 - 66 + 33 - 63 . . . up to n terms , then find p, given Sp = 0.
The petrol consumption rate of a new model car 'Palto' depends on its speed and may be described by the adjoining graph :
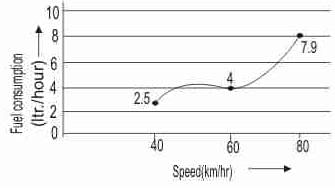
Q. Manasa makes the 200 km trip from Mumbai to Pune at a steady speed of 60 km per hour. What is the amount of petrol consumed for the journey ?



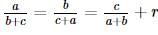 then r can not take any value except except :
then r can not take any value except except :