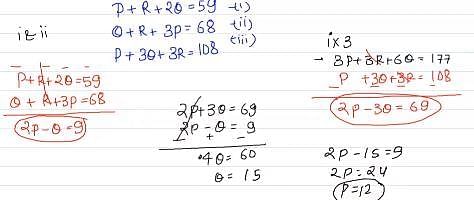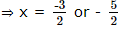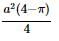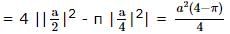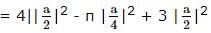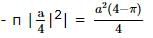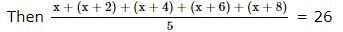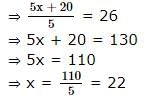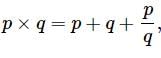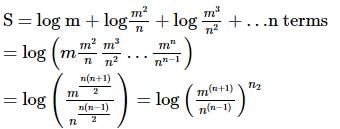All Courses
Get the App Signup / Login
Sign in Open App
CAT Exam  >  CAT Tests  >  CAT Practice Test - 34 - CAT MCQ

CAT Practice Test - 34 - CAT MCQ


Test Description

30 Questions MCQ Test - CAT Practice Test - 34

CAT Practice Test - 34 for CAT 2024 is part of CAT preparation. The CAT Practice Test - 34 questions and answers have been prepared according to the CAT exam syllabus.The CAT Practice Test - 34 MCQs are made for CAT 2024 Exam. Find important definitions, questions, notes, meanings, examples, exercises, MCQs and online tests for CAT Practice Test - 34 below.
Solutions of CAT Practice Test - 34 questions in English are available as part of our course for CAT & CAT Practice Test - 34 solutions in Hindi for CAT course. Download more important topics, notes, lectures and mock test series for CAT Exam by signing up for free. Attempt CAT Practice Test - 34 | 100 questions in 180 minutes | Mock test for CAT preparation | Free important questions MCQ to study for CAT Exam | Download free PDF with solutions
CAT Practice Test - 34 - Question 1
Save

If the ages of P and R are added to twice the age of Q, the total becomes 59. If the ages Q and R are added to thrice the age of P, the total become 68. And, if the age of P is added to thrice the age of Q and twice the age of R, the total becomes 91. What is the age of P?

Detailed Solution for CAT Practice Test - 34 - Question 1

Let the ages of P, Q and R be x, y and z years respectively.
Then x + 2y + z = 59 .....(1)
3x + y + z = 68 .....(2)
x + 3y + 2z = 91 .....(3)
Solving these equations, we get x = 12
Hence age of P is 12 years.

CAT Practice Test - 34 - Question 2
Save

If 2x + 3x + z = 25, x + y + z = 14 and x + y = z. Then what is the value of x?

Detailed Solution for CAT Practice Test - 34 - Question 2

Given, x + y = z. 
x + y + z = 14
z + z = 14
2z = 14
z = 7
2x + 3x + z = 25
5x + 7 = 25
5x = 18
x = 18/5
 

1 Crore+ students have signed up on EduRev. Have you? Download the App
CAT Practice Test - 34 - Question 3
Save

Which one of the following conditions must p, q and r satisfy so that the following system of linear simultaneous equations has at least one solution, such that p + q + r ≠ 0
x + 2y - 3z = p 
2x + 6y - 11z = q 
x - 2y + 7z = r

Detailed Solution for CAT Practice Test - 34 - Question 3

It is given that p + q + r ≠ 0
Multiply the first equation by 5, second by -2 and third by -1, the coefficients of x, y and z all add up to zero.
5x + 10y - 15z = 5p
-4x - 12y + 22z = -2q
-x + 2y - 7z = -r
Adding all three equations:
5p - 2q - r = 0

CAT Practice Test - 34 - Question 4
Save

In the given questions two equations numbered I and II are given. You have to solve both the equations and give answer.

I. 2x2 - 7x + 3 = 0
II. 2y2 - 7y + 6 = 0
Detailed Solution for CAT Practice Test - 34 - Question 4

I. 2x2 - 7x + 3 = 0
⇒ 2x2 - 6x - x + 3 = 0
⇒ 2x (x - 3) - 1 (x - 3) = 0
⇒ (2x - 1) (x - 3) = 0
⇒ x = 1212 or 3
II. 2y2 - 7y + 6 = 0
⇒ 2y2 - 4y - 3y + 6 = 0
⇒ 2y (y - 2) - 3 (y - 2) = 0
⇒ (y - 2) (2y - 3) = 0
⇒ y = 2 or 3/2

CAT Practice Test - 34 - Question 5
Save

I. 4x2 + 16x + 15 = 0
II. 2y2 + 3y + 1 = 0
Detailed Solution for CAT Practice Test - 34 - Question 5

I. 4x2 + 16x + 15 = 0
⇒ 4x2 + 10x + 6x + 15 = 0
⇒ 2x (2x + 5) + 3 (2x + 5) = 0
⇒ (2x + 3) (2x + 5) = 0


II. 2y2 + 3y + 1 = 0
⇒ 2y2 + 2y + y + 1 = 0
⇒ 2y (y + 1) + 1 (y + 1) = 0
⇒ (y + 1) (2y + 1) = 0

CAT Practice Test - 34 - Question 6
Save

A rectangular sheet of paper, when halved by folding it at the mid point of its longer side, results in a rectangle whose longer and shorter sides are in the same proportion as the longer and shorter sides of the original rectangle. If the shorter side of the original rectangle is 2, what is the area of the smaller rectangle ?
CAT Practice Test - 34 - Question 7
Save

Consider two different cloth-cutting processes. In the first one, n circular cloth pieces are cut from a square cloth piece of side a in the following steps : the original square of side a is divided into n smaller squares, not necessarily of the same size; then a circle of maximum possible area is cut from each of the smaller squares. In the second process, only one circle of maximum possible area is cut from the square of side a and the process ends there. The cloth pieces remaining after cutting the circles are scrapped in both the processes. The ratio of the total area of scrap cloth generated in the former to that in the latter is
Detailed Solution for CAT Practice Test - 34 - Question 7

The area of total scrap in second process of cutting the cloth = a2 - π (a/2)2 = 

Now by the First process of cutting the cloth:
Let us divide the big square in four equal squares of side a/2. Then the area of total scrap

 

So required ratio = 1:1
Again divide the big square in 7 small square as
Show in figure

Now total area of scrap

So required ratio = 1:1

CAT Practice Test - 34 - Question 8
Save

The average of five continuous even numbers is 26. The quarter of the sum of highest and lowest number is .....
Detailed Solution for CAT Practice Test - 34 - Question 8

Let the numbers be x, x + 2, x + 4, x + 6, x + 8



lowest no = 22 
highest no = 22 + 8 = 30

quarter of sum of highest and lowest no is

CAT Practice Test - 34 - Question 9
Save

If

    

then  8 x 2 is?
Detailed Solution for CAT Practice Test - 34 - Question 9

8×2

= 8+2+8/2

= 10+4

=14
 

CAT Practice Test - 34 - Question 10
Save

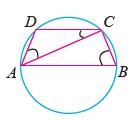
In the given figure, AB is diameter of the circle and points C and D are on the circumference such that ∠CAD = 30°and ∠CBA = 70°. What is the measure of ∠ACD?
Detailed Solution for CAT Practice Test - 34 - Question 10

According to theorem the angle subtended by a diameter on the circumference of a circle is 90°

∠ACB = 90°

 

Angle subtended by chord AC on major segment = ∠ABC = 70°

 

Angle subtended on minor segment = 180–70 = 110° = ∠ADC

 

As sum of angles of triangle ADC = 180°

 

∠ACD = 180–30–110 = 40°

CAT Practice Test - 34 - Question 11
Save

What is the distance in cm between two parallel chords of lengths 32 cm and 24 cm in a circle of radius 20 cm ?
Detailed Solution for CAT Practice Test - 34 - Question 11

For either right triangle OPA or OPB:
c² = a² + b²
(length of hypotenuse OA or OB)² = (length of OP)² + (length of AP or BP)²
(20 cm)² = (h₁)² + (16 cm)²
400 cm² = (h₁)² + 256 cm²
400 cm² ‒ 256 cm² = (h₁)² + 256 cm² ‒ 256 cm²
144 cm² = (h₁)²
(h₁)² = 144 cm² since equality is symmetric, i.e., if a = b, then b = a.
Now, taking the square root of both sides, we have:
h₁= ±√(144) cm
h₁= ±12 cm. Since we physically can’t have a negative distance, then:
h₁ = 12 cm.
Now, finding distance h₂ and then distance d:
For either right triangle OQC or OQD:
c² = a² + b²
(length of hypotenuse OC or OD)² = (length of OQ)² + (length of CQ or DQ)²
(20 cm)² = (h₂)² + (12 cm)²
400 cm² = (h₂)² + 144 cm²
400 cm² ‒ 144 cm² = (h₂)² + 144 cm² ‒ 144 cm²
256 cm² = (h₂)²
(h₂)² = 256 cm² since equality is symmetric, i.e., if a = b, then b = a.
Now, taking the square root of both sides, we have:
h₂= ±√(256) cm
h₂= ±16 cm. Since we physically can’t have a negative distance, then:
h₂ = 16 cm.
Lastly, finding the desired distance “d” between parallel chords AB and CD:
d = h₁ + h₂
= 12 cm + 16 cm
d = 28 cm

CAT Practice Test - 34 - Question 12
Save

If x, xy, xy2 are the sides of a triangle, where x and y are real numbers and y≥1y≥1, then which of the following is the value that y cannot take?
CAT Practice Test - 34 - Question 13
Save

A man invests Rs. 3000 at the rate of 5% per annum. How much more should he invest at the rate of 8%, so that he can earn a total of 6% per annum?
Detailed Solution for CAT Practice Test - 34 - Question 13

Present rate of interest = 5% (Cheaper quantity)
New rate of interest = 8% (Dearer Quantity)
Mean rate of interest = 6%
Ratio of Dearer Value : Cheaper Value = m-c : d-m = 6-5 : 8-6 = 1 : 2
Dearer Value = Rs.3000/2 = Rs.1500

CAT Practice Test - 34 - Question 14
Save

The real number x when added to its inverse gives the minimum value of the sum at x equal to
Detailed Solution for CAT Practice Test - 34 - Question 14

CAT Practice Test - 34 - Question 15
Save

A zookeeper counted the heads of the animals in a zoo and found it to be 80. When he counted the legs of the animals he found it to be 260. If the zoo had either pigeons or horses, how many horses were there in the zoo?
Detailed Solution for CAT Practice Test - 34 - Question 15

Let the number of horses = x
Then the number of pigeons = 80 – x
Each pigeon has 2 legs and each horse has 4 legs
Therefore, total number of legs = 4x + 2(80 − x) = 260
⇒ 4x + 160 – 2x = 260
⇒ 2x = 100
⇒ x = 50

CAT Practice Test - 34 - Question 16
Save

There are 50 integers a1, a2,....,a50, not all of them neccessarily different. Let the greatest integer of these 50 integers be referred to as G, and the smallest integer be referred to as L. The integers a1 through a24form sequence S1, and the rest form sequence S2. Each member of S1 is less than or equal to each member of S2.

Q. All values in S1 are changed in sign, while those in S2 remain unchanged. Which of the following statements is true ?
Detailed Solution for CAT Practice Test - 34 - Question 16

sequence 1= {a1,a2 ,,, ......................... , a24} where a1<a2<a3<....................... <a24
sequence2 ={a25,a26,.......................... ,a50} where a25>a26>.....................>a50
 and by given condition that each element of seq1 should be less than equal to seq2 element.
so smallest element of sequence 2 (which is a50) should be greater than equal to largest element of sequence 1(which is a24) 
so,possible sequences :
           SEQ 1                                                        SEQ 2
1,2,3,............................ 24                49, 48,47,....................................., 24

CAT Practice Test - 34 - Question 17
Save

There are 50 integers a1, a2,....,a50, not all of them neccessarily different. Let the greatest integer of these 50 integers be referred to as G, and the smallest integer be referred to as L. The integers a1 through a24form sequence S1, and the rest form sequence S2. Each member of S1 is less than or equal to each member of S2.

Q. Elements of S1 are in ascending order, and those of S2 are in descending order. a24 and a25 are interchanged then which of the following statements is true ?
Detailed Solution for CAT Practice Test - 34 - Question 17

sequence 1= {a1,a2 ,,, ......................... , a24} where a1<a2<a3<....................... <a24
sequence2 ={a25,a26,.......................... ,a50} where a25>a26>.....................>a50
 and by given condition that each element of seq1 should be less than equal to seq2 element.
so smallest element of sequence 2 (which is a50) should be greater than equal to largest element of sequence 1(which is a24) 
so,possible sequences :

           SEQ 1                                                        SEQ 2
1,2,3,............................ 24                49, 48,47,....................................., 24 
OR 
1,2,3,.............................24               50,49,48,........................................,25
so if we exchange a24 and a25 seq 1 will be in ascending mode . but seq 2 will not be in descending order .
 

CAT Practice Test - 34 - Question 18
Save

There are 50 integers a1, a2,....,a50, not all of them neccessarily different. Let the greatest integer of these 50 integers be referred to as G, and the smallest integer be referred to as L. The integers a1 through a24form sequence S1, and the rest form sequence S2. Each member of S1 is less than or equal to each member of S2.

Q. Every element of S1 is made greater than or equal to every element of S2 by adding to each element of S1 a integer x. Then, x cannot be less than :
CAT Practice Test - 34 - Question 19
Save

It is given that 5% increase in X always means 3% increase in Y and 5% increase in Y always impliies 2.5% increase in Z.

Q. Relationship between X and Z could be
CAT Practice Test - 34 - Question 20
Save

The maximum value of 3cosθ + 4sinθ is
Detailed Solution for CAT Practice Test - 34 - Question 20

The maximum value of 3cosθ + 4sinθ
= [32 + 42]1/2
= (25)1/2
​= 5
 

CAT Practice Test - 34 - Question 21
Save

There are three boxes, each of which has an equal number of red, blue as well as green balls in it. Now an equal number of balls are drawn from each box. What is the minimum number of balls that have to be drawn from each box to ensure that at least three similarly colored balls are obtained ?
CAT Practice Test - 34 - Question 22
Save

In a room there are 7 persons. The chance that two of them were born on the same day of the week is
CAT Practice Test - 34 - Question 23
Save

A merchant buys two articles for Rs.600. He sells one of them at a profit of 22% and the other at a loss of 8% and makes no profit or loss in the end. What is the selling price of the article that he sold at a loss?
Detailed Solution for CAT Practice Test - 34 - Question 23

Let C1 be the cost price of the first article and C2 be the cost price of the second article
Let the first article be sold at a profit of 22%, while the second one be sold at a loss of 8%
We know, C1 + C2 = 600
The first article was sold at a profit of 22% = C1 + (22/100) C1 = 1.22C1
The second article was sold at a loss of 8%
Therefore, the selling price of the second article = C2 - (8/100)C2 = 0.92C2
The total selling price of the first and second article = 1.22C1 + 0.92C2
As the merchant did not make any profit or loss in the entire transaction, his combined selling price of article 1 and 2 is the same as the cost price of article 1 and 2
Therefore, 1.22C1 + 0.92C2 = C1 + C2 = 600
As C1 + C2 = 600, C2 = 600 - C1. Substituting this in 1.22C1 + 0.92C2 = 600, we get
1.22C1 + 0.92(600 - C1) = 600
or 1.22C1 - 0.92C1 = 600 - 0.92 × 600
or 0.3C1 = 0.08 × 600 = 48

or C1 = 48/(0.3) = 160

If C1 = 160, then C2 = 600 - 160 = 440
The item that is sold at loss is article 2
The selling price of article 2 = 0.92 × C2 = 0.92 × 440 = 404.80

CAT Practice Test - 34 - Question 24
Save

For all 'x', x²+2ax+(10-3a)>0, then the interval in which 'a' lies is
Detailed Solution for CAT Practice Test - 34 - Question 24

x = - B +- (√(B2 - 4.A.C)/2A)
Since x is Real, thus, B2 - 4AC i.e the term under sqrt, must be >0
comparing the equation you gave with the original Ax2+Bx+C = 0, we get A = 1, B = 2a, C = (10 - 3a).
So, (2a)2 - 4.1.(10-3a) >0
simplifying we get,
(a+5)(a-2)>0
-5 < a < 2

CAT Practice Test - 34 - Question 25
Save

In a kilometre race, A can give B a start of 100 m or 15 seconds. How long does A take to complete the race?
Detailed Solution for CAT Practice Test - 34 - Question 25

Suppose , A completes the race in X Seconds, B completes in Y seconds & Race has 1000 m track.

If A can give B a start of 100m & still win,

X-(900/1000)*Y<=0

hence, X<=0.9Y

If A can give B a start of 15 Seconds & still win,

X-(Y-15)<0

hence, X<= Y-15

0.9Y= Y-15

0.1Y=15

Y=150 Seconds

X=135 Seconds

CAT Practice Test - 34 - Question 26
Save

Sweta, Swarna, Sneha and Soumya and four sisters who have an agreements that they share all snaks among themselves. One day, uncle Prem gave a box of cookies of Sweta. Since the other sisters were not around. Swetha divided the cookies into four parts, ate her share and put the rest into the box. As she was closing the box. Swarna came in. She took all the cookies from the box and divided them into four equal parts. Sweta and Swarna ate one part each and put the rest in the box. Just then, Sneha walked in. She took all the cookies from the box, divided them into four equal parts. The three of them ate their respective shares and put the rest into the box. Later, when Soumya came, she divided all the cookies into four equal parts and all four sisters are their respectives shares. In total, Soumya ate 3 cookies.

Q. How many cookies, in total, did Sneha eat?
CAT Practice Test - 34 - Question 27
Save

What is the sum of 'n' terms in the series : log m + log(m2/n) + log(m3/n2) + log(m4/n3) + ....
Detailed Solution for CAT Practice Test - 34 - Question 27

CAT Practice Test - 34 - Question 28
Save

Sin (2 cos⁻¹ (3/5)) =
Detailed Solution for CAT Practice Test - 34 - Question 28

sin[2cos-1(3/5)]
= 2sin(cos-1(3/5)cos(cos-1(3/5)
= 2(3/5)[1-(3/5)2]1/2
= 6/4*4/5
= 24/25

CAT Practice Test - 34 - Question 29
Save

Ram and Shyam attempted to solve a quadratic equation. Ram made a mistake in writing down the constant term. He ended up with the roots (4, 3). Shyam made a mistake in writing down the coefficient of x. He got the root as (3, 2). What will be the exact roots of the original quadratic equation?
CAT Practice Test - 34 - Question 30
Save

Two friends, Sachin and Sourav, with speeds of 20m/s and 15m/s respectively are chasing a thief who is running away from them with the speed of 10m/s. After sometime Sachin observed that Sourav has been left behind so he reduced his speed to 15m/s and at the same instant Sourav increased his speed to 20m/s. If, after two minutes of this, both of them caught thief, then find the initial distance between them and the thief. It is given that they started chasing from the same point at the same time.
View more questions
Information about CAT Practice Test - 34 Page
In this test you can find the Exam questions for CAT Practice Test - 34 solved & explained in the simplest way possible. Besides giving Questions and answers for CAT Practice Test - 34, EduRev gives you an ample number of Online tests for practice

Top Courses for CAT

Download as PDF

Top Courses for CAT

Important Questions for CAT Practice Test - 34

Find all the important questions for CAT Practice Test - 34 at EduRev.Get fully prepared for CAT Practice Test - 34 with EduRev's comprehensive question bank and test resources. Our platform offers a diverse range of question papers covering various topics within the CAT Practice Test - 34 syllabus. Whether you need to review specific subjects or assess your overall readiness, EduRev has you covered. The questions are designed to challenge you and help you gain confidence in tackling the actual exam. Maximize your chances of success by utilizing EduRev's extensive collection of CAT Practice Test - 34 resources.

CAT Practice Test - 34 MCQs with Answers

Prepare for the CAT Practice Test - 34 within the CAT exam with comprehensive MCQs and answers at EduRev. Our platform offers a wide range of practice papers, question papers, and mock tests to familiarize you with the exam pattern and syllabus. Access the best books, study materials, and notes curated by toppers to enhance your preparation. Stay updated with the exam date and receive expert preparation tips and paper analysis. Visit EduRev's official website today and access a wealth of videos and coaching resources to excel in your exam.

Online Tests for CAT Practice Test - 34

Practice with a wide array of question papers that follow the exam pattern and syllabus. Our platform offers a user-friendly interface, allowing you to track your progress and identify areas for improvement. Access detailed solutions and explanations for each test to enhance your understanding of concepts. With EduRev's Online Tests, you can build confidence, boost your performance, and ace CAT Practice Test - 34 with ease. Join thousands of successful students who have benefited from our trusted online resources.
© EduRev
Education Revolution
Signup to see your scores go up within 7 days!
Access 1000+ FREE Docs, Videos and Tests
Takes less than 10 seconds to signup