Test: JEE Main 35 Year PYQs- Simple Harmonic Motion (Oscillations) - JEE MCQ
30 Questions MCQ Test - Test: JEE Main 35 Year PYQs- Simple Harmonic Motion (Oscillations)
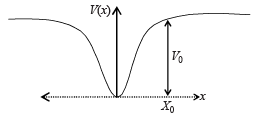
When a particle of mass m moves on the x-axis in a potential of the form V(x) = kx2 it performs simple harmonic motion. The corresponding time period is proportional to 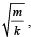 as can be seen easily using dimensional analysis. However, the motion of a particle can be periodic even when its potential energy increases on both sides of x = 0 in a way different from kx2 and its total energy is such that the particle does not escape to infinity. Consider a particle of mass m moving on the x-axis. Its potential energy is V(x) = αx4 (α > 0) for |x| near the origin and becomes a constant equal to V0 for |x| > X0 (see figure).
as can be seen easily using dimensional analysis. However, the motion of a particle can be periodic even when its potential energy increases on both sides of x = 0 in a way different from kx2 and its total energy is such that the particle does not escape to infinity. Consider a particle of mass m moving on the x-axis. Its potential energy is V(x) = αx4 (α > 0) for |x| near the origin and becomes a constant equal to V0 for |x| > X0 (see figure).
Q. If the total energy of the particle is E, it will perform periodic motion only if
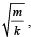 as can be seen easily using dimensional analysis. However, the motion of a particle can be periodic even when its potential energy increases on both sides of x = 0 in a way different from kx2 and its total energy is such that the particle does not escape to infinity. Consider a particle of mass m moving on the x-axis. Its potential energy is V(x) = αx4 (α > 0) for |x| near the origin and becomes a constant equal to V0 for |x| > X0 (see figure).
as can be seen easily using dimensional analysis. However, the motion of a particle can be periodic even when its potential energy increases on both sides of x = 0 in a way different from kx2 and its total energy is such that the particle does not escape to infinity. Consider a particle of mass m moving on the x-axis. Its potential energy is V(x) = αx4 (α > 0) for |x| near the origin and becomes a constant equal to V0 for |x| > X0 (see figure).
When a particle of mass m moves on the x-axis in a potential of the form V(x) = kx2 it performs simple harmonic motion. The corresponding time period is proportional to 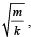 as can be seen easily using dimensional analysis. However, the motion of a particle can be periodic even when its potential energy increases on both sides of x = 0 in a way different from kx2 and its total energy is such that the particle does not escape to infinity. Consider a particle of mass m moving on the x-axis. Its potential energy is V(x) = αx4 (α > 0) for |x| near the origin and becomes a constant equal to V0 for |x| > X0 (see figure).
as can be seen easily using dimensional analysis. However, the motion of a particle can be periodic even when its potential energy increases on both sides of x = 0 in a way different from kx2 and its total energy is such that the particle does not escape to infinity. Consider a particle of mass m moving on the x-axis. Its potential energy is V(x) = αx4 (α > 0) for |x| near the origin and becomes a constant equal to V0 for |x| > X0 (see figure).

Q. For periodic motion of small amplitude A, the time period T of this particle is proportional to
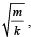 as can be seen easily using dimensional analysis. However, the motion of a particle can be periodic even when its potential energy increases on both sides of x = 0 in a way different from kx2 and its total energy is such that the particle does not escape to infinity. Consider a particle of mass m moving on the x-axis. Its potential energy is V(x) = αx4 (α > 0) for |x| near the origin and becomes a constant equal to V0 for |x| > X0 (see figure).
as can be seen easily using dimensional analysis. However, the motion of a particle can be periodic even when its potential energy increases on both sides of x = 0 in a way different from kx2 and its total energy is such that the particle does not escape to infinity. Consider a particle of mass m moving on the x-axis. Its potential energy is V(x) = αx4 (α > 0) for |x| near the origin and becomes a constant equal to V0 for |x| > X0 (see figure).
When a particle of mass m moves on the x-axis in a potential of the form V(x) = kx2 it performs simple harmonic motion. The corresponding time period is proportional to 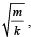 as can be seen easily using dimensional analysis. However, the motion of a particle can be periodic even when its potential energy increases on both sides of x = 0 in a way different from kx2 and its total energy is such that the particle does not escape to infinity. Consider a particle of mass m moving on the x-axis. Its potential energy is V(x) = αx4 (α > 0) for |x| near the origin and becomes a constant equal to V0 for |x| > X0 (see figure).
as can be seen easily using dimensional analysis. However, the motion of a particle can be periodic even when its potential energy increases on both sides of x = 0 in a way different from kx2 and its total energy is such that the particle does not escape to infinity. Consider a particle of mass m moving on the x-axis. Its potential energy is V(x) = αx4 (α > 0) for |x| near the origin and becomes a constant equal to V0 for |x| > X0 (see figure).

Q. The acceleration of this particle for |x| > X0 is
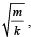 as can be seen easily using dimensional analysis. However, the motion of a particle can be periodic even when its potential energy increases on both sides of x = 0 in a way different from kx2 and its total energy is such that the particle does not escape to infinity. Consider a particle of mass m moving on the x-axis. Its potential energy is V(x) = αx4 (α > 0) for |x| near the origin and becomes a constant equal to V0 for |x| > X0 (see figure).
as can be seen easily using dimensional analysis. However, the motion of a particle can be periodic even when its potential energy increases on both sides of x = 0 in a way different from kx2 and its total energy is such that the particle does not escape to infinity. Consider a particle of mass m moving on the x-axis. Its potential energy is V(x) = αx4 (α > 0) for |x| near the origin and becomes a constant equal to V0 for |x| > X0 (see figure).
Phase space diagrams are useful tools in analyzing all kinds of dynamical problems. They are especially useful in studying the changes in motion as initial position and momenum are changed.
Here we consider some simple dynamical systems in one dimension. For such systems, phase space is a plane in which position is plotted along horizontal axis and momentum is plotted along vertical axis. The phase space diagram is x(t) vs. p(t) curve in this plane. The arrow on the curve indicates the time flow. For example, the phase space diagram for a particle moving with constant velocity is a straight line as shown in the figure. We use the sign convention in which positon or momentum upwards (or to right) is positive and downwards (or to left) is negative.
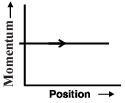
Q. The phase space diagram for a ball thrown vertically up from ground is
Phase space diagrams are useful tools in analyzing all kinds of dynamical problems. They are especially useful in studying the changes in motion as initial position and momenum are changed.
Here we consider some simple dynamical systems in one dimension. For such systems, phase space is a plane in which position is plotted along horizontal axis and momentum is plotted along vertical axis. The phase space diagram is x(t) vs. p(t) curve in this plane. The arrow on the curve indicates the time flow. For example, the phase space diagram for a particle moving with constant velocity is a straight line as shown in the figure. We use the sign convention in which positon or momentum upwards (or to right) is positive and downwards (or to left) is negative.

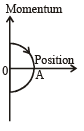
Q. The phase space diagram for simple harmonic motion is a circle centered at the origin. In the figure, the two circles represent the same oscillator but for different initial conditions, and E1 and E2 are the total mechanical energies respectively. Then
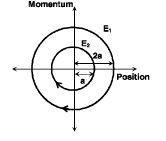
Phase space diagrams are useful tools in analyzing all kinds of dynamical problems. They are especially useful in studying the changes in motion as initial position and momenum are changed.
Here we consider some simple dynamical systems in one dimension. For such systems, phase space is a plane in which position is plotted along horizontal axis and momentum is plotted along vertical axis. The phase space diagram is x(t) vs. p(t) curve in this plane. The arrow on the curve indicates the time flow. For example, the phase space diagram for a particle moving with constant velocity is a straight line as shown in the figure. We use the sign convention in which positon or momentum upwards (or to right) is positive and downwards (or to left) is negative.

Q. Consider the spring-mass system, with the mass submerged in water, as shown in the figure. The phase space diagram for one cycle of this system is

In a simple harmonic oscillator, at the mean position
If a spring has time period T, and is cut into n equal parts, then the time period of each part will be
A child swinging on a swing in sitting position, stands up, then the time period of the swing will
A mass M is suspended from a spring of negligible mass. The spring is pulled a little and then released so that the mass executes SHM of time period T. If the mass is increased by m, the time period becomes 5T/3. Then the ratio of m/M is
Two particles A and B of equal masses are suspended from two massless springs of spring of spring constant k1 and k2, respectively. If the maximum velocities, during oscillation, are equal, the ratio of amplitude of A and B is
The length of a simple pendulum executing simple harmonic motion is increased by 21%. The percentage increase in the time period of the pendulum of increased length is
The displacement of a particle varies according to the relation x = 4(cos πt + sinπt). The amplitude of the particle is
A body executes simple harmonic motion. The potential energy (P.E), the kinetic energy (K.E) and total energy (T.E) are measured as a function of displacement x. Which of the following statements is true ?
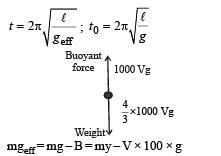
The bob of a simple pendulum executes simple harmonic motion in water with a period t, while the period of oscillation of the bob is t0 in air. Neglecting frictional force of water and given that the density of the bob is (4 / 3) x 1000 kg/m3 .
What relationship between t and t0 is true
A particle at the end of a spring executes S.H.M with a period t1. while the corresponding period for another spring is t2. If the period of oscillation with the two springs in series is T then
The total energy of a particle, executing simple harmonic motion is where x is the displacement from the mean position, hence total energy is independent of x.
A particle of mass m is attached to a spring (of spring constant k) and has a natural angular frequency ω0. An external force F(t) pr opor tion al to cos ωt (ω ≠ ω0) is applied to th e oscillator. The time displacement of the oscillator will be proportional to
In forced oscillation of a particle the amplitude is maximum for a frequency ω1 of the force while the energy is maximum for a frequency ω2 of the force; then
Two simple harmonic motions are represented by the equations  = 0.1 cos πt . The phase difference of the velocity of particle 1 with respect to the velocity of particle 2 is
= 0.1 cos πt . The phase difference of the velocity of particle 1 with respect to the velocity of particle 2 is
The function sin2 (ωt) represents
The bob of a simple pendulum is a spherical hollow ball filled with water. A plugged hole near the bottom of the oscillating bob gets suddenly unplugged. During observation, till water is coming out, the time period of oscillation would
If a simple harmonic motion is represented by 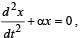 its time period is
its time period is
Th e maximum velocity of a particle, executin g simple harmonic motion with an amplitude 7 mm, is 4.4 m/s. The period of oscillation is
Starting from the origin a body oscillates simple harmonically with a period of 2 s. After what time will its kinetic energy be 75% of the total energy?
Two springs, of force constants k1 and k2 are connected to a mass m as shown. The frequency of oscillation of the mass is f. If both k1 and k2 are made four times their original values, the frequency of oscillation becomes
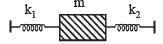
A particle of mass m executes simple harmonic motion with amplitude a and frequency v. The average kinetic energy during its motion from the position of equilibrium to the end is
The displacement of an object attached to a spring and executing simple harmonic motion is given by x = 2 × 10–2 cos πt metre.The time at which the maximum speed first occurs is
A point mass oscillates along the x-axis according to the law x = x0 cos(ωt -π / 4) . If the acceleration of the particle is written as a = A cos(wt +δ) ,then
If x, v and a denote the displacement, the velocity and the acceleration of a particle executing simple harmonic motion of time period T, then, which of the following does not change with time?




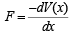
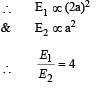
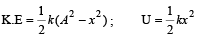
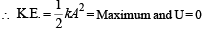
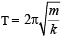 where m is the mass of oscillating body.
where m is the mass of oscillating body.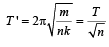
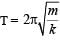 where m is the mass of
where m is the mass of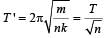
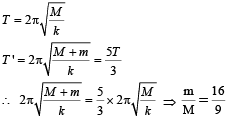
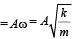
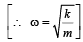
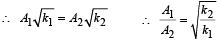
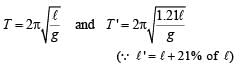
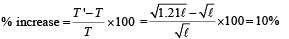
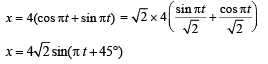
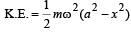
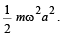
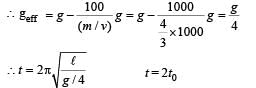
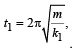
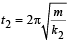
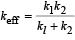
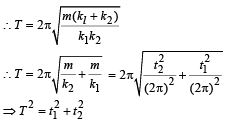
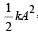 = constant, where A = amplitude
= constant, where A = amplitude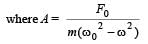


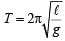

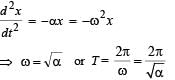
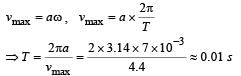
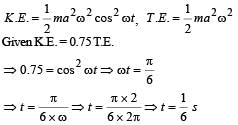

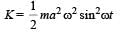
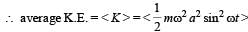
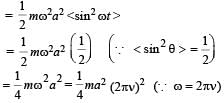
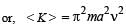
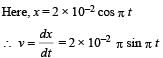
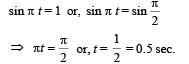
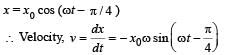
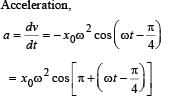
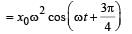 ...(1)
...(1)
















