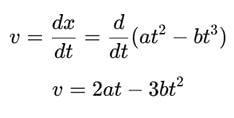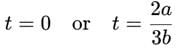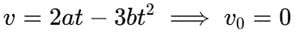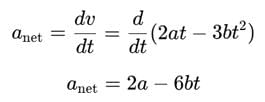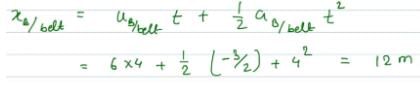Test: Motion in a Straight Line - 3 - Grade 11 MCQ
25 Questions MCQ Test - Test: Motion in a Straight Line - 3
The displacement x of a particle depend on time t as x = at2 - bt3
A particle has intial velocity 10 m/s. It moves due to constant retarding force along the line of velocity which produces a retardation of 5 m/s2. Then -
Mark the correct statements for a particle going on a straight line
A particle initially at rest is subjected to two forces. One is constant, the other is a retarding force proportion at to the particle velocity. In the subsequent motion of the particle
In a shaping operation, the average cutting speed is ( Stroke length S, Number of strokes per minute N, Quick return ratio R)
Which of the following statements are true for a moving body?
Let v and a denote the velocity and acceleration respectively of a body
A tennis ball is thrown straight up and caught at the same height. Which of the following can describe the motion of the ball when it reaches the apex?
Velocity-time graph for a car is semicircle as shown here. Which of the following is correct :
The figure shows the velocity (v) of a particle plotted against time (t)
A block is thrown with a velocity of 2 ms-1 (relative to ground) on a belt, which is moving with velocity 4 ms-1 in opposite direction of the initial velocity of block. If the block stops slipping on the belt after 4 sec of the throwing then choose the correct statements(s)
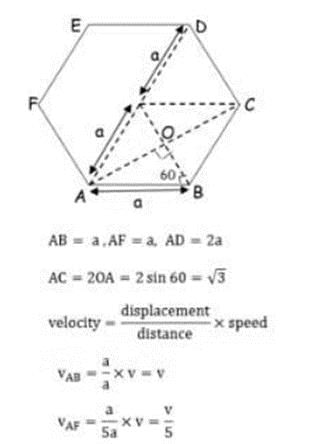
A particle moves with constant speed v along a regular hexagon ABCDEF in the same order. Then the magnitude of the average velocity for its motion from A to -
An observer moves with a constant speed along the line joining two stationary objects. He will observe that the two objects
A man on a rectilinearly moving cart, facing the direction of motion, throws a ball straight up with respect to himself
A projectile of mass 1 kg is projected with a velocity of m/s such that it strikes on the same level as the point of projection at a distance of
m. Which of the following options are incorrect.
The v-t graph of the particle is correctly shown by
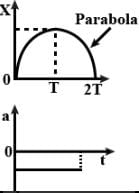
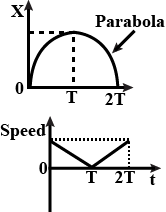
The x-t graph of the particle moving along a straight line is shown in figure.
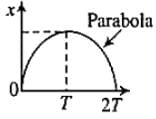
The a-t graph of the particle is correctly shown by
The speed-time graph of the particle is correctly shown by
The figure shows a velocity-time graph of a particle moving along a straight line
Choose the incorrect statement. The particle comes to rest at
A train covers 60 miles between 2 p.m. and 4 p.m. How fast was it going at 3 p.m.?
The figure shows a velocity-time graph of a particle moving along a straight line
If the particle starts from the position x0 = -15 m, then its position at t = 2s will be
The figure shows a velocity-time graph of a particle moving along a straight line
The maximum of displacement of the particle is
The figure shows a velocity-time graph of a particle moving along a straight line
The total distance travelled by the particle is
The figure shows a velocity-time graph of a particle moving along a straight line
The correct displacement-time graph of the particle is shown as