Test: Solid Mechanics- 3 - Civil Engineering (CE) MCQ
10 Questions MCQ Test - Test: Solid Mechanics- 3
For state, a stress  mohr circle will have center and radius is
mohr circle will have center and radius is
 mohr circle will have center and radius is
mohr circle will have center and radius is Which of the following is the most appropriate theory of failure for mild steel?
Consider the following statements:
1. On planes having maximum and minimum principal stress, there will be no tangential stress.
2. Shear stresses on mutually perpendicular planes are numerically equal.
3. Maximum shear stress is numerically equal to half the sum of the maximum and minimum principal stress
Which of the following statement is/are correct –
A cube is subjected to equal tensile stress on the three faces. If the yield stress of the material is ‘σy’ and poison ratio ‘μ’ then based on strain energy theory, the maximum tensile stress will be
At a point in a steel member, major principal stress is 1000 kg/cm2, and minor principal stress is compressive. If uniaxial tensile yield stress is 1500 kg/cm2, then the magnitude of minor principal stress at which yielding will commence, according to maximum shearing stress theory is
The principal stresses developed at a point are +30, -30, 0 MPa. Using shear strain energy theory, a factor of safety obtained is √6. What is yield stress of the material?
In a structural member, there are perpendicular tensile stresses of 100 N/mm2. What is the equivalent stress in simple tension, according to the maximum principal strain theory? (Poisson’s ratio = 0. 50)
In metal forming operation when the material has just started yielding, the principal stresses are σ1 = +180 MPa, σ2 = -100 MPa, σ3 = 0. Following the von Mises criterion, the yield stress is ________ MPa.
The Mohr’s circle given below corresponds to which one of the following stress condition.

2D stress matrix at a point is given below:
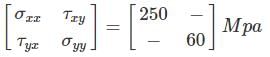
If the maximum shear stress is 200 Mpa. The value of τxy will be ________ Mpa.




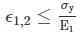 For no failure in uni – axial loading.
For no failure in uni – axial loading. For no failure in tri – axial loading.
For no failure in tri – axial loading. For design, Here, ϵ = Principal strain
For design, Here, ϵ = Principal strain








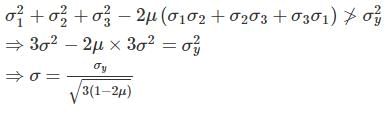
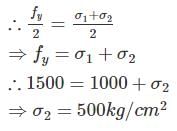




 And centre of Mohr’s circle is at a distance,
And centre of Mohr’s circle is at a distance,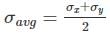 from the origin. Here it is in origin.
from the origin. Here it is in origin.

















