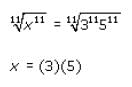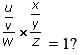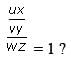GMAT Full Mock Test- 1 - GMAT MCQ
30 Questions MCQ Test - GMAT Full Mock Test- 1
If –2<a<11 and 3<b<12, then which of the following is NOT true?
a, b, and c are integers and a < b < c. S is the set of all integers from a to b, inclusive. Q is the set of all integers from b to c, inclusive. The median of set S is (3/4)b. The median of set Q is (7/8)c. If R is the set of all integers from a to c, inclusive, what fraction of c is the median of set R?
| 1 Crore+ students have signed up on EduRev. Have you? Download the App |
a, b, and c are positive integers. If a, b, and c are assembled into the six-digit number abcabc, which one of the following must be a factor of abcabc?
A certain club has exactly 5 new members at the end of its first week. Every subsequent
week, each of the previous week's new members (and only these members) brings exactly x new
members into the club. If y is the number of new members brought into the club during the
twelfth week, which of the following could be y?
Directions: The data sufficiency problem consists of a question and two statements, labeled (1)
and (2), in which certain data are given. You have to decide whether the data given in the
statements are sufficient for answering the question. Using the data given in the statements plus
your knowledge of mathematics and everyday facts (such as the number of days in July or the
meaning of counterclockwise), you must indicate whether
Q.
x is a positive number. If 9x + 9x+1 + 9x+2 + 9x+3 + 9x+4 + 9x+5 = y, is y divisible by 5?
1) 5 is a factor of x.
2) x is an integer.
If the range of the set of numbers {150, 90, 125, 110, 170, 155, x, 100, 140} is 95, which of thefollowing could be x?
Frances can complete a job in 12 hours, and Joan can complete the same job in 8 hours.Frances starts the job at 9 a.m., and stops working at 3 p.m. If Joan starts working at 4 p.m. tocomplete the job, at what time is the job finished?
Directions: The data sufficiency problem consists of a question and two statements, labeled (1)
and (2), in which certain data are given. You have to decide whether the data given in the
statements are sufficient for answering the question. Using the data given in the statements plus
your knowledge of mathematics and everyday facts (such as the number of days in July or the
meaning of counterclockwise), you must indicate whether
Q.
A, B, C, D, and E are airline pilots with very busy travel schedules. Given that D is able to meet at
any time that B cannot meet, do the schedules of A, B, C, D, and E allow three of these five
individuals to meet together for two uninterrupted hours?
(1) Pilots A and C, who cannot meet together, are not able to end any meeting during the AM
hours of any weekday.
(2) Pilots B and E, who can never meet for longer than 2 uninterrupted hours, are only available
to meet for two straight hours starting at 10:30 PM on any weekday and not ending during the AM
hours of any weekend day.
1/212 + 2/213 + 22/214 + 23/215 =
( answer to the nearest approximation)
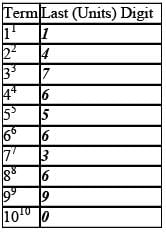
If n is an integer greater than 0, what is the remainder when 912n+3 is divided by 10?
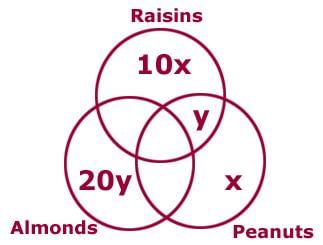
Each of 435 bags contains at least one of the following three items: raisins, almonds, andpeanuts. The number of bags that contain only raisins is 10 times the number of bags that containonly peanuts. The number of bags that contain only almonds is 20 times the number of bags thatcontain only raisins and peanuts. The number of bags that contain only peanuts is one-fifth thenumber of bags that contain only almonds. 210 bags contain almonds. How many bags containonly one kind of item?
Directions: The data sufficiency problem consists of a question and two statements, labeled (1)
and (2), in which certain data are given. You have to decide whether the data given in the
statements are sufficient for answering the question. Using the data given in the statements plus
your knowledge of mathematics and everyday facts (such as the number of days in July or the
meaning of counterclockwise), you must indicate whether
Q.
What is the probability that  and
and 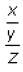 are reciprocal fractions?
are reciprocal fractions?
(1) v, w, y, and z are each randomly chosen from the first 100 positive integers.
(2) The product (u)(x) is the median of 100 consecutive integers.
If n is an integer greater than 5.3, then n! must be divisible by which of the following numbers?
Directions: The data sufficiency problem consists of a question and two statements, labeled (1)
and (2), in which certain data are given. You have to decide whether the data given in the
statements are sufficient for answering the question. Using the data given in the statements plus
your knowledge of mathematics and everyday facts (such as the number of days in July or the
meaning of counterclockwise), you must indicate whether
Q.
what is population of the village
1. 7/11 of the village comprises of married people
2. 200 widows comprises 10% of the singles population
Directions: The data sufficiency problem consists of a question and two statements, labeled (1)
and (2), in which certain data are given. You have to decide whether the data given in the
statements are sufficient for answering the question. Using the data given in the statements plus
your knowledge of mathematics and everyday facts (such as the number of days in July or the
meaning of counterclockwise), you must indicate whether
Q.
The sum of the ages of A, B and C is 137 years. What is C’s age
1. the sum of the ages of A and C is 91 years
2. the sum of the ages of B and C is 104 years
Directions: The data sufficiency problem consists of a question and two statements, labeled (1)
and (2), in which certain data are given. You have to decide whether the data given in the
statements are sufficient for answering the question. Using the data given in the statements plus
your knowledge of mathematics and everyday facts (such as the number of days in July or the
meaning of counterclockwise), you must indicate whether
Q.
Is the number x is divisible by 9.
1. The number x can be obtained by taking the difference between a number and another one obtained by reversing the digits.
2. The sum of the digits of x is divisible by 9.
Directions: The data sufficiency problem consists of a question and two statements, labeled (1)
and (2), in which certain data are given. You have to decide whether the data given in the
statements are sufficient for answering the question. Using the data given in the statements plus
your knowledge of mathematics and everyday facts (such as the number of days in July or the
meaning of counterclockwise), you must indicate whether
Q.
In an election how many votes are cast.
1. the winning candidate gets 54% of the total votes
2. the winning candidate wins by 800
Directions: The data sufficiency problem consists of a question and two statements, labeled (1)
and (2), in which certain data are given. You have to decide whether the data given in the
statements are sufficient for answering the question. Using the data given in the statements plus
your knowledge of mathematics and everyday facts (such as the number of days in July or the
meaning of counterclockwise), you must indicate whether
Q.
Is (y/x)*(1+x)2 > 2y
1. xy > 0
2. x + y > 5
a,b are integers, Is b exactly divisible by 20?
Statement I: a / 20 + b / 20 is an integer
Statement II: a / 7 + b / 20 is an integer
In a school, 35% girls and 19% boys participated in singing. Number of students in the school is 700. How many boys are there in the school?
Statement I: Number of boys are more than 200
Statement II: More than 190 students participated
A printer numbered consecutively the pages of a book, beginning with 1 on the first page. Innumbering the pages, he had to print a total of 187 digits. Find the number of pages inthe book.
In a drawer of shirts, 8 r blue, 6 r green, and 4 r magenta. If Mason draws 2 shirts at random,what is the probability that at least one of the shirts he draws will be blue?
Which of the following CANNOT yield an integer when divided by 10?
(i) Product of two prime numbers
(ii) An integer less than 10
(iii) Sum of three consecutive integers
(iv) An odd integer
A number, K, is a positive integer with the special property that 3 times its unit is equal to 2 timesits 10 digit. How many such numbers exist between 10 & 99?
If two digit integer M and N are positive and have same digits, but in reverse order, which of thefollowing cannot be the sum of M and N.
Directions: The data sufficiency problem consists of a question and two statements, labeled (1)
and (2), in which certain data are given. You have to decide whether the data given in the
statements are sufficient for answering the question. Using the data given in the statements plus
your knowledge of mathematics and everyday facts (such as the number of days in July or the
meaning of counterclockwise), you must indicate whether
Q.
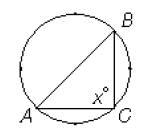
In the figure above, does x = 90?
(1) The length of AC is less than the length of BC.
(2) The length of AB is one-fourth the circumference of the circle.


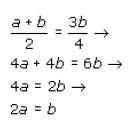
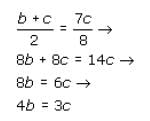
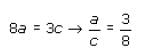
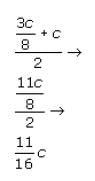
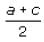 . We can use the ratio
. We can use the ratio 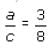 to substitute 3c/8 for a:
to substitute 3c/8 for a: