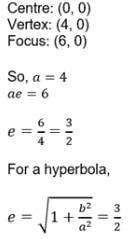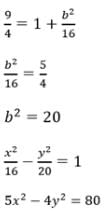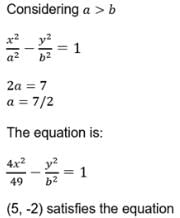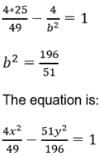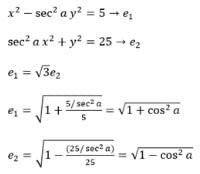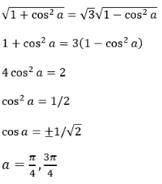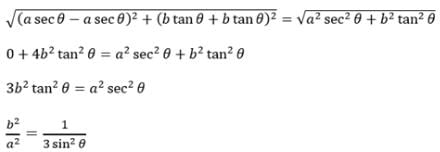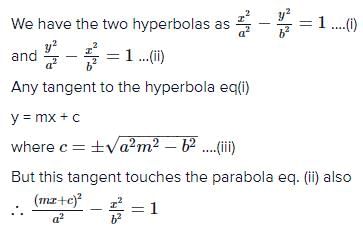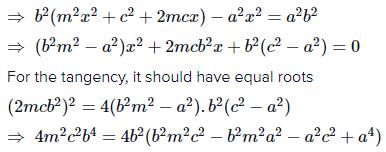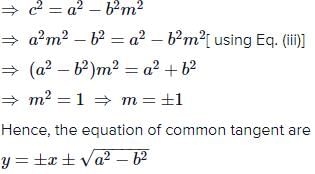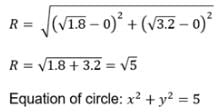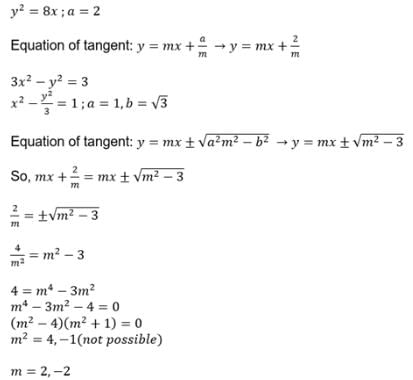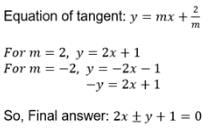Test: Hyperbola- 1 - JEE MCQ
20 Questions MCQ Test - Test: Hyperbola- 1
The locus of the point of intersection of the lines √3x - y - 4√3k = 0 and √3kx + ky - 4√3 = 0 for different values of k is
| 1 Crore+ students have signed up on EduRev. Have you? Download the App |
If the latus rectum of an hyperbola be 8 and eccentricity be 3/√5 then the equation of the hyperbola is
If the centre, vertex and focus of a hyperbola be (0, 0), (4, 0) and (6, 0) respectively, then the equation of the hyperbola is
The equation of the hyperbola whose foci are (6, 5), (–4, 5) and eccentricity 5/4 is
The vertices of a hyperbola are at (0, 0) and (10, 0) and one of its foci is at (18, 0). The equation of the hyperbola is
The length of the transverse axis of a hyperbola is 7 and it passes through the point (5, –2). The equation of the hyperbola is
If the eccentricity of the hyperbola x2 – y2 sec2 a = 5 is (√3) times the eccentricity of the ellipse x2 sec2 a + y2 = 25, then a value e of a is
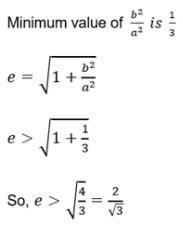
AB is a double ordinate of the hyperbola such that DAOB (where `O' is the origin) is an equilateral triangle, then the eccentricity e of the hyperbola satisfies
The equation of the tangent lines to the hyperbola x2 – 2y2 = 18 which are perpendicular to the line y = x are
The equation to the common tangents to the two hyperbolas and
are
Locus of the feet of the perpendiculars drawn from either foci on a variable tangent to the hyperbola 16y2 – 9x2 = 1 is
The ellipse 4x2 + 9y2 = 36 and the hyperbola 4x2 – y2 = 4 have the same foci and they intersect at right angles then the equation of the circle through the points of intersection of two conics is
The equation of the common tangent to the parabola y2 = 8x and the hyperbola 3x2– y2 = 3 is
Equation of the chord of the hyperbola 25x2 – 16y2 = 400 which is bisected at the point (6, 2) is
If the product of the perpendicular distances from any point on the hyperbola of eccentricity e = √3 on its asymptotes is equal to 6, then the length of the transverse axis of the hyperbola is
If the normal to the rectangular hyperbola xy = c2 at the point `t' meets the curve again at `t1' then t3t1 has the value equal to
Area of triangle formed by tangent to the hyperbola xy = 16 at (16, 1) and co-ordinate axes equals
Locus of the middle points of the parallel chords with gradient m of the rectangular hyperbola xy = c2 is