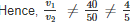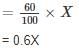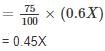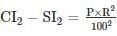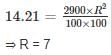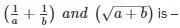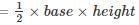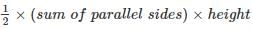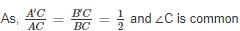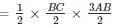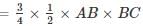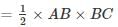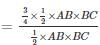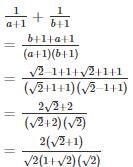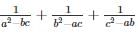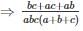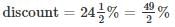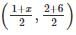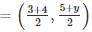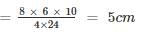Practice Test: Quantitative Aptitude - 7 - SSC CGL MCQ
25 Questions MCQ Test - Practice Test: Quantitative Aptitude - 7
A hollow sphere of internal and external radius 3 cm and 5 cm respectively is melted into a solid right circular cone of diameter 8 cm. The height of the cone is
A and B can together do a piece of work in 28 days. If A, B and C can together finish the work in 14 days, how long will C take to do the work by himself?
| 1 Crore+ students have signed up on EduRev. Have you? Download the App |
Two cars are moving with speeds v1, v2 towards a crossing along two roads. If their distances from the crossing be 40 metres and 50 metres at an instant of time then they do not collide if their speeds are such that
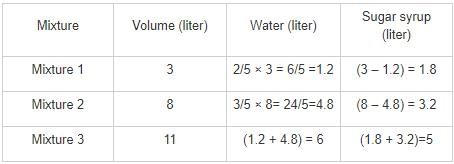
2/5 Part of a mixture of 3 l is water and the rest is sugar syrup. Another mixture of 8 l contains 3/5 part water and the rest is sugar syrup. It both mixture are mixed together then what will be the ratio of water & sugar syrup in the new mixture?
A wire is bent in the form of an equilateral triangle encloses a region having area of 121√3 cm². If the same wire is rebent in the form of a circle, its radius will be:
In a class of 50 students, 20 students had an average score of 70 and remaining had an average score of 50. What is the average score of the class?
In a factory 60% of the workers are above 30 years and of these 75% are males and the rest are females. If there are 1350 male workers above 30 years, the total number of workers in the factory is
The difference between simple interest and compound interest for 2 years on the sum Rs. 2900 at a certain rate is Rs. 14.21. What is annual rate of interest?
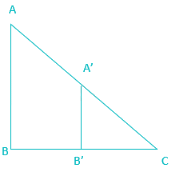
ABC is a right angled triangle, B being the right angle. Midpoints of BC and AC are respectively B’ and A’. The ratio of the area of the quadrilateral AA’ B’B to the area of the triangle ABC is
The cost of making an article is divided between materials, labor and overheads in the ratio 3 : 4 : 2. If the cost of material is Rs.33.60 the cost of article is
If a = √2 + 1, b = √2 – 1, then the value of 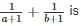
If ‘a’ and ‘b’ are two odd positive integers, by which of the following is (a4 – b4) always divisible?
If (x - 2) and (x + 3) are the factors of x2 + k1x + k2 then
The heights of two poles are 180 m and 60 m respectively. If the angle of elevation of the top of the first pole form the foot of the second pole is 60°, what is the angle of elevation of the top of the second pole form the foot of the first?
If 3 sin θ + 5 cos θ = 5, then the value of 5 sin θ – 3 cos θ wil be
A shopkeeper sold an item for Rs. 1,510 after giving a discount of 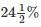 and there by incurred a loss of 10%. Had he sold the item without discount, his net profit would have been
and there by incurred a loss of 10%. Had he sold the item without discount, his net profit would have been
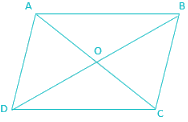
If A(1, 2), B(4, y), C(x, 6) and D(3, 5) are the vertices of a parallelogram taken in order, then find the values of x and y.
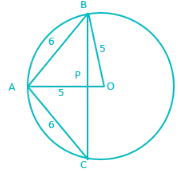
In a circle of radius 5 cm, AB and AC are two equal chords such that AB = AC = 6 cm. The length of BC (in cm) is
In a Δ PQR, ∠RPQ = 90°, PR = 8 cm and PQ = 6 cm, then the radius of the circumcircle of Δ PQR is
Directions: Study the following table carefully and answer the questions.
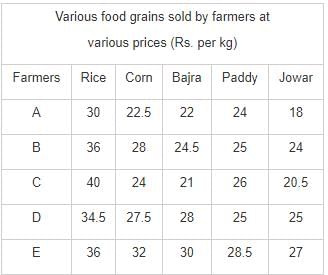
Q. If farmer D and farmer E, both sell 240 kg of Bajara each, what would be the respective ratio of their earnings?
Directions: Study the following table carefully and answer the questions.
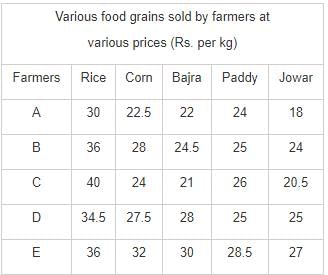
Q. What is the average price per kg of Bajra sold by all the farmers together?
Directions: Study the following table carefully and answer the questions.
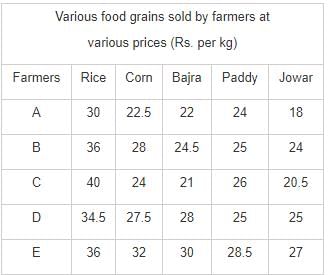
Q. If farmer A sells 350 kg of rice, 150 kg of corn and 250 kg of jowar, how much would he earn?
Directions: Study the following table carefully and answer the questions.
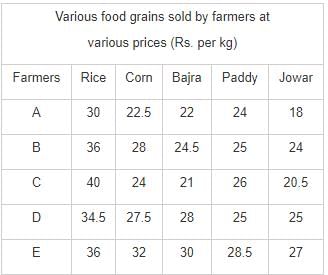
Q. Earnings on 150 kg of paddy sold by farmer B are approximately what percent of the earnings on the same amount of rice sold by the same farmer?


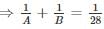

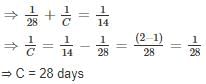
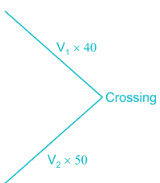
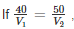 then they will collide i.e. cars will reach at the same time.
then they will collide i.e. cars will reach at the same time.